若在每一水平下重复试验次数不同，假定在Ai水平下进行了mi次实验，那么方差分析仍可进行，只是在计算中有( )改动。A．此时n=∑miB．此时SA的计算公式改为C．此时SA的计算公式改为D．此时将表示所有n=rm个数据和改为表示n=mi个数据和E．此时将Se=ST-SA改为Se=SA-ST

题目

若在每一水平下重复试验次数不同，假定在Ai水平下进行了mi次实验，那么方差分析仍可进行，只是在计算中有( )改动。

A．此时n=∑mi

B．此时SA的计算公式改为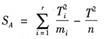

C．此时SA的计算公式改为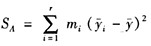

D．此时将表示所有n=rm个数据和改为表示n=mi个数据和

E．此时将Se=ST-SA改为Se=SA-ST

相似考题

1.设有单因子试验，因子A有r个水平，在Ai水平下进行mi次重复试验，则误差偏差平方和的自由度为( )。[*]A．fe＝r-1B．fe＝rm-rC．D．以上都不对

2.若在每一水平下重复实验次数不同，那么方差分析仍可进行，只是在计算中应有所改动，以下需要变动的量是( )。A．因子A平方和SAB．误差e的平方和SeC．总计T的平方和STD．误差e的自由度fe

3.在单因子方差分析中，因子A有3个水平，每个水平下各做4次重复试验，已算得因子 A的平方和SA=42，总平方和ST=69，则误差平方和Se=( )。A．3B．9C．27D．18

4.在单因子试验中，方差分析的基本假设包括（ ）。A.在水平Ai下试验指标Yi服从正态分布B.在不同的水平下，试验指标Yi的方差相等C.各试验指标Yij相互独立D.在水平Ai下，指标Yi的均值相等E.在水平Ai下试验指标Yi不一定服从正态分布

参考答案和解析
正确答案：ABC
解析：若在每一水平下重复实验次数不同，假定在Ai水平下进行了mi次实验，那么方差分析仍可进行，只是在计算中有两个改动：一是此时n=∑mi，二是SA的计算公式改为。
更多“ 若在每一水平下重复试验次数不同，假定在Ai水平下进行了mi次实验，那么方差分析仍可进行，只是在计算中有( )改动。A．此时n=∑miB．此时SA的计算公式改为C．此时SA的计算公式改为D．此时将表示所有n=rm个”相关问题

  • 第1题：

    在单因子试验中A有2个水平，每一水平下进行了3次试验，并求得因子与误差平方和分别为 SA＝56.29，Ssub>E＝48.77，那么检验用F比是( )。

    A．4.62

    B．4.65

    C．6.15

    D．6.54


    正确答案：B
    解析：由于因子A有2个水平，即r＝2，所以有：fA＝2-1＝1，又在每一水平下进行了3次重复试验，即m＝3，所以fe＝2(3-1)＝4，现在SA＝56.29，Se＝48.77，则MSA＝SA/fA＝56.29，MSe＝Se/fe＝12.1925，从而F＝MSA/MS=4.65

  • 第2题：

    现已知因子A有3个水平，在实验中每一水平下进行了4次重复实验，并求得因子与误差平方和分别为SA=58.35，Se=46.85。在给定α＝0.05的水平上因子A的显著性质为( )。

    A．显著的

    B．不显著的

    C．总是显著的

    D．总是不显著的


    正确答案：A
    解析：由于因子A有3个水平，即r=3，所以fA=r-1=3-1=2，又在每一水平下进行了4次重复实验，即m=4，所以fe=r(m-1)=3x(4-1)=9。由题意知SA=58.35，Se=46.85，则MSA=SA/fA=58.35/2=29.175，MSe=Se/fe=46.85/9=5.21，从而F=MSA/MSe=5.60。对于给定的α＝0.05，则1－α=0.95，从F分布表查得F0.95(2，9)=4.26，则F=5.60＞4.26，所以在α＝0.05水平上，因子且是显著的。

  • 第3题：

    设有单因子试验，因子A有r个水平，在Ai水平下进行mi次重复试验，则误差平方和Se的自由度为( )。

    A．fe=r-1

    B．

    C．

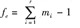
    D．fe=n-1


    正确答案：B
    解析：ST、SA、Se的自由度分别用fT、fA、fe表示，则有：fT=fA+fe。其中，fT=n-1=

  • 第4题：

    在单因子方差分析中，因子A是二水平的，在每一水平下重复进行了3次试验，结果如表2.1-2所示，则下列结论正确的有( )。

    A．误差平方和Se=4

    B．因子A的平方和SA=24

    C．误差均方MSe=2

    D．因子A的均方MSA=12

    E．统计量F=24


    正确答案：ABE
    解析：

  • 第5题：

    在单因子方差分析中，因子A是二水平的，在每一水平下重复进行了3次试验，结果如表所示，则下列结论正确的有（ ）。

    A.误差平方和Se =4 B.因子A的平方和SA =24
    C.误差均方MSe =2 D.因子A的均方MSA= 12
    E.统计量F=24


    答案：A,B,E
    解析：

  • 第6题：

    单因子方差分析中，因子A有3个水平，每个水平下的重复试验次数分别为7，6，5。据试验结果算得因子A的平方和SA = 97. 65，误差平方和Se=40.75，由此可算得FA比为（ ）。
    A. 1. 20 B. 2. 40

    C. 17. 97 D. 48. 83


    答案：C
    解析：
    。F=MSA/MSe = (97. 65/2)/(40.75/15) = 17. 97。

  • 第7题：

    在单因子方差分析中，因子A有3个水平，每个水平下各做4次重复试验，已算 得因子A的平方和SA=42，总平方和ST = 69，则误差平方和Se = ( )。

    A. 3 B. 9
    C. 27 D. 18


    答案：C
    解析：
    。Se = ST —SA = 69 —42 = 27。水平数、重复次数均为干扰条件。

  • 第8题：

    在单因子方差分析，如果因子A有r个水平，在每一水平下进行m次试验，那么误差平方和的自由度为（ ）。
    A. r - 1 B. m-1 C. rm-1 D. r( m - 1)


    答案：D
    解析：
    误差平方和的自由度fe=fT-fA= (rm -1) -(r-1) = r(m-1)。

  • 第9题：

    若在每一水平下重复试验次数不同，假定在Ai水平下进行了mi次实验，那么方差分析仍可进行，只是在计算中有（ ）改动。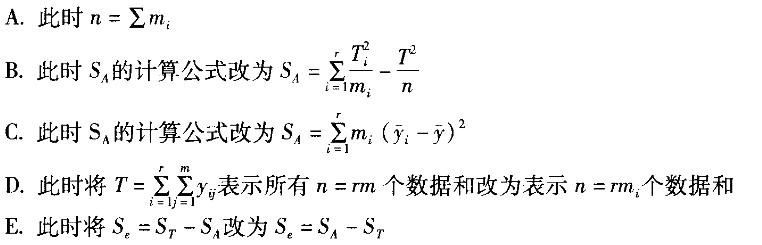


    答案：A,B,C
    解析：
    若在每一水平下重复实验次数不同，假定在Ai水平下进行了mi次实验，那么方差分析仍可进行，只是在计算中有两个改动：一是此时n=Σmi，二是SA的计算公式改为：

  • 第10题：

    在单因子试验中A有2个水平，每一水平下进行了3次试验，并求得因子与误差平方和分别为SA =56.29，Se=48. 77，那么检验用F比是（ ）。
    A. 4. 62 B. 4. 65 C. 6. 15 D. 6. 54


    答案：A
    解析：
    由于因子A有2个水平，即r=2，所以有fA=r - 1=2-1 =1；又在每一水平下进行了3次重复试验，即m=3，所以fe=r(m-1) =2(3 -1) = 4；已知SA =56.29，Se=48. 77，则MSA = SA/fA = 56. 29，MSe = Se/fe = 12. 1925，故F = MSA/ MSe=4. 62。

  • 第11题：

    单选题
    现已知因子A有3个水平，在实验中每一水平下进行了4次重复实验，并求得因子与误差平方和分别为SA=58.35，Se=46.85。在给定α=0.05的水平上因子A的显著性质为（　　）。
    A

    显著的

    B

    不显著的

    C

    总是显著的

    D

    总是不显著的


    正确答案： B
    解析：
    由于因子A有3个水平，即r=3，所以fA=r-1＝3-1=2，又在每一水平下进行了4次重复实验，即m=4，所以fe=r（m-1）＝3×（4-1）=9。由题意知SA=58.35，Se=46.85，则MSA=SA/fA=58.35／2=29.175，MSe=Se/fe=46.85／9=5.21，从而F=MSA／MSe=5.60。对于给定的α=0.05，则1-α=0.95，从F分布表查得F0.95（2，9）=4.26，则F=5.60＞4.26，所以在α=0.05水平上，因子A是显著的。

  • 第12题：

    填空题
    在任意一次试验中，事件A服从0～1分布，那么在相同的条件下，进行n次独立、重复试验，用X表示这n次试验中事件A发生的次数，那么X服从（）。

    正确答案： 二项
    解析： 暂无解析

  • 第13题：

    在单因子方差分析，如果因子A有r个水平，在每一水平下进行m次试验，那么误差平方和的自由度为( )。

    A．r-1

    B．m-1

    C．rm-1

    D．r(m-1)


    正确答案：D
    解析：误差平方和的自由度fe=fT-fA(em-1)-(r-1)=r(m-1)。

  • 第14题：

    在一个单因子方差分析中，因子有3个水平，在每一水平下的试验数据如表2.1—3所示，则下列结论正确的是( )。

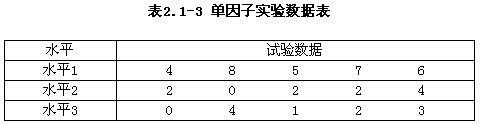
    A．SA=26.67

    B．SA=53.33

    C．Se=14

    D．Se=28

    E．ST=81.33


    正确答案：BDE
    解析：各水平下数据的和分别为T1=30，T2=10，T3=10，均值分别为=2,，所以Se=ST-SA=28。

  • 第15题：

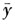    在单因子方差分析中，如果因子A有r个水平，在每一水平下进行m次试验，试验结果用yij表示，i=1，2，…，r；j=1，2，…，m；表示第i水平下试验结果的平均，表示试验结果的总平均，那么误差平方和为( )。


    正确答案：B
    解析：误差平方和用组内平方和表示。

  • 第16题：

    现已知因子A有3个水平，在实验中每一水平下进行了4次重复实验，并求得因子与误差平方和分别为SA=58. 35，Se=46. 85 。在给定a =0.05的水平上因子A的显著性质为( )。
    A.显著的 B.不显著的 C.总是显著的 D.总是不显著的


    答案：A
    解析：
    由于因子A有3个水平，即r=3，所以fA = r - 1=3-1 =2，又在每一水平下进行了4次重复实验，即m=4，所以fe = r(m-1) /e=3x(4-1 =9。由题意知SA=58. 35，Se=46. 85 ，则 MSA= SA/fA = 58.35/2 = 29. 175，MSe =Se /fe = 46. 85/9 =5.21，从而 F = MSA/MSe =5.6。对于给定的a=0.05，则1-a=0.95，从F分布表査得F0.95 (2，9)= 4.26，则F = 5.60>4.26，所以在a =0. 05水平上，因子A是显著的。

  • 第17题：

    在单因子方差分析中，因子A有3个水平，每个水平下各做4次重复试验，已算得因子A的平方和SA=42，总平方和ST=69，则误差平方和Se=( )。
    A. 3 B. 9 C. 27 D. 18


    答案：C
    解析：
    因为SA +Se=ST，所以Se=ST -SA=69-42=27。

  • 第18题：

    在一个单因子方差分析中，因子有3个水平，在每一水平下的试验数据如表所示，则下列结论正确的是（ ）。

    A. SA =26. 67 B. SA =53. 33 C. Se=14 D. Se=28
    E. ST=81. 33


    答案：B,D,E
    解析：

  • 第19题：

    若在每一水平下重复实验次数不同，那么方差分析仍可进行，只是在计算中应有所改动，以下需要变动的量是（ ）。
    A.因子A平方和SA B.误差e的平方和Se
    C.总计T的平方和STD.误差e的自由度fe


    答案：A
    解析：
    若在每一水平下重复实验次数不同，假定在Ai水平下进行了mi次实验，那么方差分析仍可进行，只是在计算中有两个改动：一是此时n=Σmi，二是SA的计算公式改为: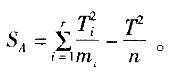

  • 第20题：

    设有单因子试验，因子A有r个水平，在Ai水平下进行mi次重复试验，则误差平方和Se的自由度为（ ）。


    答案：B
    解析：
    ST、SA 、Se的自由度分别用fT、fA、fe表示，则有：fT =fe+fA，其中fT=n-1=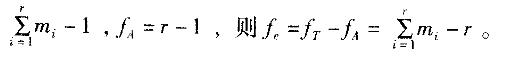

  • 第21题：

    在一个单因子方差分析中，因子有4个水平，每一水平的数据如表所示，则下列结论正确的有（ ）。

    A. SA =53. 33 B.SA = 60 C. Se = 18 D. Se=28
    E. ST =88


    答案：B,D,E
    解析：
    各水平下的数据和分别是 ：30， 10, 10，10，数据总和为60，各水平下数据的

  • 第22题：

    在任意一次试验中，事件A服从0～1分布，那么在相同的条件下，进行n次独立、重复试验，用X表示这n次试验中事件A发生的次数，那么X服从（）。


    正确答案:二项

  • 第23题：

    单选题
    在单因子试验中A有2个水平，每一水平下进行了3次试验，并求得因子与误差平方和分别为SA=56.29，SE=48.77，那么检验用F比是(　　)。
    A

    4.62

    B

    4.65

    C

    6.15

    D

    6.54


    正确答案： D
    解析： 56.29/12.1925＝4.62

相关内容