方差分析的一般步骤为( )。A．计算因子A的每一水平下数据的和T1，T2，…，Tr及总和TB．计算各类数据的平方和。C．依次计算ST，SA，SeD．计算各均方差及F比值，并列出方差分析表E．对于给定的显著性水平α，将求得的F比与F分布表中的F1-α(FA，fe)比较，当F＞ F1-α(fA，fe)时认为因子A是不显著的，否则认为因子A是显著的

题目

方差分析的一般步骤为( )。

A．计算因子A的每一水平下数据的和T1，T2，…，Tr及总和T

B．计算各类数据的平方和。

C．依次计算ST，SA，Se

D．计算各均方差及F比值，并列出方差分析表

E．对于给定的显著性水平α，将求得的F比与F分布表中的F1-α(FA，fe)比较，当F＞ F1-α(fA，fe)时认为因子A是不显著的，否则认为因子A是显著的

相似考题

1.方差分析的步骤是以下哪些()A、求平方和并计算自由度B、计算均方和F值C、查F值表进行F检验D、作出判断E、陈列方差分析表

2.若在每一水平下重复实验次数不同，那么方差分析仍可进行，只是在计算中应有所改动，以下需要变动的量是( )。A．因子A平方和SAB．误差e的平方和SeC．总计T的平方和STD．误差e的自由度fe

3.在单因子方差分析中，因子A有3个水平，每个水平下各做4次重复试验，已算得因子 A的平方和SA=42，总平方和ST=69，则误差平方和Se=( )。A．3B．9C．27D．18

4.方差分析的一般步骤包括()。A、建立原假设和备择假设B、选择显著性水平C、选择检验统计量D、给出判别准则E、选择样本，计算结果，做出判断

更多“ 方差分析的一般步骤为( )。A．计算因子A的每一水平下数据的和T1，T2，…，Tr及总和TB．计算各类数据的平方和。C．依次计算ST，SA，SeD．计算各均方差及F比值，并列出方差分析表E．对于给定的显著性水平α”相关问题

  • 第1题：

    在单因子方差分析中，因子A有4个水平，各水平下的重复试验数分别为8，5，7，6。根据试验结果已算得因子A的平方和SA=167.53，误差平方和Se=337.17。由此可算得统计量F的值为( )。

    A．2.73

    B．5.23

    C．3.64

    D．6.30


    正确答案：C
    解析：由题意可知因子水平数r=4，试验共有n=8+5+7+6=26个数据，所以总离差平方和ST的自由度fT=n-1=26-1=25，因子A的平方和SA的自由度为fA=r-1=3，误差平方和的自由度fe=fT-fA=25-3=22，所以MSA=SA/fA=167.53/3≈55.84，MSe=Se/fe=337.17/22≈15.33，所以统计量F=MSA/MSe=55.84/15.33≈3.64。

  • 第2题：

    在正交试验中，对试验结果进行方差分析时，方差分析表中的表头内容包括( )。

    A．数据来源

    B．偏差平方和及其自由度

    C．因素水平表

    D．均方和及F比

    E．水平数


    正确答案：ABD
    解析：方差分析表的表头内容包括：数据来源、平方和、自由度、均方和及F比。

  • 第3题：

    若在每一水平下重复试验次数不同，假定在Ai水平下进行了mi次实验，那么方差分析仍可进行，只是在计算中有( )改动。

    A．此时n=∑mi

    B．此时SA的计算公式改为

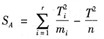
    C．此时SA的计算公式改为

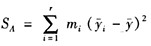
    D．此时将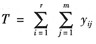表示所有n=rm个数据和改为表示n=mi个数据和

    E．此时将Se=ST-SA改为Se=SA-ST


    正确答案：ABC
    解析：若在每一水平下重复实验次数不同，假定在Ai水平下进行了mi次实验，那么方差分析仍可进行，只是在计算中有两个改动：一是此时n=∑mi，二是SA的计算公式改为。

  • 第4题：

    在单因子方差分析中，因子A有3个水平，每个水平下各做4次重复试验，已算得因子A的平方和SA=42，总平方和ST=69，则误差平方和Se=( )。
    A. 3 B. 9 C. 27 D. 18


    答案：C
    解析：
    因为SA +Se=ST，所以Se=ST -SA=69-42=27。

  • 第5题：

    考察温度对某一化工产品得率的影响，选了五种不同的温度进行试验，在同一温度下进行了3次试验，试验结果如表所示。
    总和T = 1344,总平均为y = 89. 6, ,请利用以上数据分析下列问题。

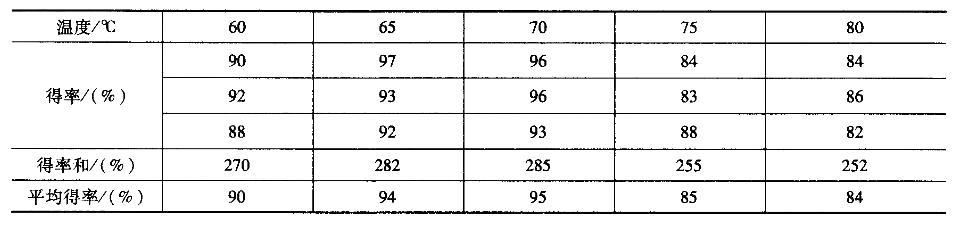
    为对数据进行方差分析，通过计算有（）。
    A.总离差平方和为ST=353. 6 B.总离差平方和为ST = 120686. 4 C.因子离差平方和为SA=303. 6 D.因子离差平方和SA为72346


    答案：A,C
    解析：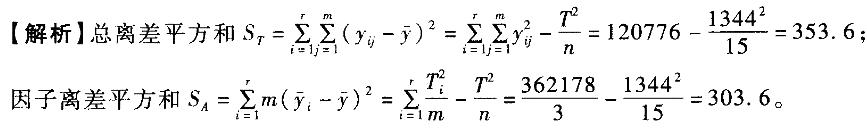

  • 第6题：

    在单因子方差分析中，因子A有3个水平，每个水平下各做4次试验，现已算得总平方和Sr= 69，因子A的平方和SA=42,则检验因子A是否显著的统计量F 的值为（ ）。
    A. 1. 56 B. 14
    C. 3 D. 7


    答案：D
    解析：

  • 第7题：

    在一个单因子方差分析中，因子有3个水平，在每一水平下的试验数据如表所示，则下列结论正确的是（ ）。

    A. SA =26. 67 B. SA =53. 33 C. Se=14 D. Se=28
    E. ST=81. 33


    答案：B,D,E
    解析：

  • 第8题：

    若在每一水平下重复实验次数不同，那么方差分析仍可进行，只是在计算中应有所改动，以下需要变动的量是（ ）。
    A.因子A平方和SA B.误差e的平方和Se
    C.总计T的平方和STD.误差e的自由度fe


    答案：A
    解析：
    若在每一水平下重复实验次数不同，假定在Ai水平下进行了mi次实验，那么方差分析仍可进行，只是在计算中有两个改动：一是此时n=Σmi，二是SA的计算公式改为: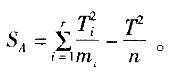

  • 第9题：

    在一个单因子方差分析中，因子有4个水平，每一水平的数据如表所示，则下列结论正确的有（ ）。

    A. SA =53. 33 B.SA = 60 C. Se = 18 D. Se=28
    E. ST =88


    答案：B,D,E
    解析：
    各水平下的数据和分别是 ：30， 10, 10，10，数据总和为60，各水平下数据的

  • 第10题：

    对于计量资料的处理方法，下列哪一项是不合适的

    A.方差分析
    B.计算率和相对比
    C.计算均数及标准差
    D.秩和检验
    E.直线相关分析

    答案：B
    解析：

  • 第11题：

    多选题
    方差分析的一般步骤为（　　）。
    A

    计算因子A的每一水平下数据的和T1，T2，…，Tr及总和T

    B

    计算各类数据的平方和∑∑y2ij，∑T2i，T2

    C

    依次计算ST，SA，Se

    D

    计算各均方差及F比值，并列出方差分析表

    E

    对于给定的显著性水平α，将求得的F比与F分布表中的F1-α（fA，fe）比较，当F＞F1-α（fA，fe）时认为因子A是不显著的，否则认为因子A是显著的


    正确答案： B,C
    解析：
    方差分析的一般步骤为：①计算因子A的每一水平下数据的和T1，T2，…，Tr及总和T；②计算各类数据的平方和∑∑y2ij，∑T2i，T2；③依次计算ST，SA，Se；④计算各均方及F比值并列出方差分析表；⑤对于给定的显著性α，将求得的F比值与F分布表中的F1-α（fA，fe）比较，当F＞F1-α（fA，fe）时认为因子A是显著的，否则认为因子A是不显著的。

  • 第12题：

    单选题
    在单因子方差分析中，因子A有3个水平，每个水平下各做4次试验，现已算得总平方和ST=69，因子A的平方和SA=42，则检验因子A是否显著的统计量F的值为（　　）。[2008年真题]
    A

    1.56

    B

    14

    C

    3

    D

    7


    正确答案： D
    解析：
    根据题意知，r=3，m=4，Se=ST-SA=69-42=27，所以fA=r-1=2，fe=r（m-1）=3×（4-1）=9，则MSA=SA/fA=42/2=21，MSe=Se/fe=27/9=3，则检验因子A是否显著的统计量F的值为：F=MSA/MSe=21/3=7。

  • 第13题：

    为对数据进行方差分析，通过计算有( )。

    A．总离差平方和为ST=353.6

    B．总离差平方和为ST=120686.4

    C．因子离差平方和为SA=303.6

    D．因子离差平方和为SA=72346


    正确答案：AC
    解析：总离差平方和公式为：，代入数据求得总离差平方和为；因子离差平方和公式为：SA=，代入数据求得因子离差平方和为=303.6。

  • 第14题：

    在单因子方差分析中，因子A是二水平的，在每一水平下重复进行了3次试验，结果如表2.1-2所示，则下列结论正确的有( )。

    A．误差平方和Se=4

    B．因子A的平方和SA=24

    C．误差均方MSe=2

    D．因子A的均方MSA=12

    E．统计量F=24


    正确答案：ABE
    解析：

  • 第15题：

    在单因子方差分析中，因子A是二水平的，在每一水平下重复进行了3次试验，结果如表所示，则下列结论正确的有（ ）。

    A.误差平方和Se =4 B.因子A的平方和SA =24
    C.误差均方MSe =2 D.因子A的均方MSA= 12
    E.统计量F=24


    答案：A,B,E
    解析：

  • 第16题：

    在有5个水平的单因子方差分析中，若每一水平下进行3次试验，且求得每一水 平下试验结果的平均值为90，94, 95, 85，84，则下列计算结果中，正确的有（）。
    A.因子平方和为303. 6 B.因子平方和为101. 2
    C.因子平方和的自由度是4 D.因子平方和的自由度是2
    E.总平方和为303. 6


    答案：A,C
    解析：

  • 第17题：

    在单因子方差分析中，因子A有2个水平，每个水平下各重复试验3次，具体数据为: 水平A1: 9, 7，8；水平A2：3，1，2，有关平方和或均方的正确计算结果有（）。
    A.因子A的平方和SA=54 B.因子A的均方MSA=27
    C.误差平方和Se =4 D.误差的均方MSe =2
    E.总平方和Sr=54


    答案：A,C
    解析：

  • 第18题：

    在单因子方差分析中，因子A有2个水平，每个水平下各重复试验3次，具体数据为：水平A1: 9，7，8；水平A2: 3，1，2。有关平方和或均方的正确计算结果有（ ）。
    A.因子A的平方和SA=54
    B.因子A的均方MSA=27
    C.误差平方和Se=4
    D.误差的均方MSe= 2
    E.总平方和ST= 54


    答案：A,C
    解析：

  • 第19题：

    在单因子方差分析中，因子A有3个水平，每个水平下各做4次重复试验，已算 得因子A的平方和SA=42，总平方和ST = 69，则误差平方和Se = ( )。

    A. 3 B. 9
    C. 27 D. 18


    答案：C
    解析：
    。Se = ST —SA = 69 —42 = 27。水平数、重复次数均为干扰条件。

  • 第20题：

    在单因子方差分析中，因子A有4个水平，各水平下的重复试验数分别为8,5, 7, 6。 根据试验结果已算得因子A的平方和SA=167.53，误差平方和Se =337. 17。由此可算得统计量F的值为（ ）。
    A. 2.73 B. 5.23 C. 3.64 D. 6.30


    答案：C
    解析：
    由题意可知因子水平数r=4，试验共有n =8+5+7+6 =26个数据，所以总离差平方和ST的自由度fT=n- 1 =26 - 1 =25，因子A的平方和SA的自由度为fA=r-1=3， 误差平方和的自由度fe =fT-fA =25 -3 =22，所以MSA=SA /fA= 167. 53/3≈55. 84，MSe =Se /fe =337. 17/22≈15. 33，所以统计量F = MSA/MSe =55. 84/15. 33≈3. 64。

  • 第21题：

    在单因子方差分析中，因子A有3个水平，每个水平下各做4次试验，现已算得总平方和ST=69，因子A的平方和SA =42，则检验因子A是否显著的统计量F的值为（ ）。
    A. 1.56 B. 14 C. 3 D. 7


    答案：D
    解析：
    根据题意知，f=3, m=4, Se = ST - SA =69 -42 =21，所以fA = r - 1 = 2，fe = r(m-1) =3x(4-1) =9，则MSA=SA /fA = 42/2 = 21，MSe =Se /fe =27/9 = 3，则检验因子A是否显著的统计量F的值为：F = MSA/MSe =21/3=7。

  • 第22题：

    多选题
    在正交试验中，对试验结果进行方差分析时，方差分析表中的表头内容包括（　　）。
    A

    数据来源

    B

    偏差平方和及其自由度

    C

    因素水平表

    D

    均方和及F比

    E

    水平数


    正确答案： A,D
    解析：
    方差分析表的表头内容包括：数据来源、平方和、自由度、均方和及F比。

  • 第23题：

    多选题
    在正交试验中，对试验结果进行方差分析时，方差分析表中的表头内容包括(　　)。
    A

    变差来源

    B

    偏差平方和及其自由度

    C

    因素水平表

    D

    均方和及F比

    E

    因子数


    正确答案： E,B
    解析： 方差分析表包括：数据来源、平方和、自由度、均方和及，比。

相关内容