设10个数据的均值x 10为9.26,如今又得到第11个数据9.92,则此11个数据的均值x 11=________。A．9.23B．9.32C．9.74D．9.59
题目
设10个数据的均值x 10为9.26,如今又得到第11个数据9.92,则此11个数据的均值x 11=________。
A．9.23
B．9.32
C．9.74
D．9.59
相似考题
更多“设10个数据的均值x 10为9.26,如今又得到第11个数据9.92,则此11个数据的均值x 11=________。A.9.23 ”相关问题
-
第1题：
假设100个数据的平均值为82.31，其中有10个数据又发生了如下增减变化：+3.52，+2.87，-4.13，+5.34，-2.87，+2.50，-3.52，+4.23，-5.04，+0.10，则新的平均值变为(26)。
A．82.34
B．82.28
C．82.61
D．85.31
正确答案：A
解析：学校里学习的平均值计算很简单，将所有数据求和再除以数据个数。在实际工作中，数据量很大，多数数据又比较集中在一定范围中，甚至大批数据都是一样的。按学校中所学的方法计算，又费时间，又容易出错。本题描述了动态的情况。数据经常变动，在短时间内，可能大部分数据没有变动，少数数据有变动，平均值当然也会有变动。如何动态地计算平均值呢?题中给出的方法是，对少数有变动的数据，指出其增减的值，将这些增减的值求和就会得到总和的增减值，将这些增减值的和除以数据的总数，就会得到平均值的增减值。在对题中给出的各数据增减值求和时，也要讲究计算方法。例如，第1个数+3.52与后面的-3.52就抵消了，这两个数就可以划去；第2个数+2.87与后面的-2.87也抵消了；第3个数-4.13与后面的数+4.23相抵后剩余+0.10；第4个数+5.34与后面的-5.04相抵后剩余+0.30；将已处理过的数划去，留下剩余数，这样再求和就方便了，从而得到3.00。因此，100个数(注意，应按100个数计算，而不是10个数)的总和将增加3.00，平均值将增加0.03。原来的平均值是82.31，新的平均值应是82.34。上述过程描述起来有点麻烦，实际做起来非常简单，比用计算机或计算器都要快，简单的心算也十分准确(用计算器还可能发生击键错误)。 -
第2题：
设X～N(μ，0.09)从中随机抽取样本量为4的样本，其样本均值为
，则总体均值μ的 0.95的置信区间为( )。
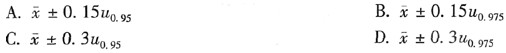正确答案：B
解析：由X～N(μ，0.09)可知该总体标准差已知，用正态分布得μ的1-α的置信区间为。所以μ的0.95的置信区间=。 -
第3题：
10个数据的均值X=105.5，现发现其中一个数据有误，错误数据为100.5，正确数据应为103.5。修正后的均值X等于（ ）。
A.105.6
B.105.8
C.106.5
D.107.5
正确答案：B
修正后的均值=(105.5×10-100.5+103.5)÷10=1058÷10=105.8。 -
第4题：
10个数据的均值X= 105. 5，现发现其中一个数据有误，错误数据为100. 5，正确 数据应为103.5。修正后的均值X等于（）。
A. 105.6 B. 105.8
C. 106.5 D. 107.5答案：B解析：。修正后的均值 x = (105. 5X10 —100. 5 + 103. 5)÷10 = 1 058÷10=105. 8。 -
第5题：
测定某产品质量特性值数据为：10、11、11、10、14、13、15、15、19、17，求其平均值X平均和极差R值？
正确答案: X平均=（10+11+11+10+14+13+15+15+19+17）/10=13.5
R=Xmax-Xmin=19-10=9
平均值X平均为13.5，极差R值为9。 -
第6题：
已知一组数据结果中，平均值为50，标准差为10，则这组数据的离散系数是（）。
- A、20%
- B、10%
- C、5%
- D、50%
正确答案:A -
第7题：
已知第一组数据的均值为5，标准差为1．58；第二组数据均值为125，标准差为2．58，则（）。
- A、第一组数据离散程度小于第二组数据
- B、第一组数据离散程度等于第二组数据
- C、第一组数据离散程度大于第二组数据
- D、以上都不对
正确答案:C -
第8题：
如果监测数据样本量较小，而数据值变化幅度较大，则水质参数选取（）
- A、监测数据的平均值
- B、监测数据的最大值
- C、平均值与最大值的均方根
- D、平均值与最大值的立方根
正确答案:C -
第9题：
单选题一组数据的标准差为10，离散系数为0.4，则该组数据的平均值为（ ）。A10
B25
C20
D4
正确答案： D解析： -
第10题：
单选题有一组数据其均值是20，对其中的每一个数据都加上10，那么得到的这组新数据的均值是（）。A20
B10
C15
D30
正确答案： D解析： 暂无解析 -
第11题：
问答题测定某产品质量特性值数据为：10、11、11、10、14、13、15、15、19、17，求其平均值X平均和极差R值？正确答案： X平均=（10+11+11+10+14+13+15+15+19+17）/10=13.5
R=Xmax-Xmin=19-10=9
平均值X平均为13.5，极差R值为9。解析： 暂无解析 -
第12题：
单选题两组数据的均值不同，但标准差相等，则（）A均值小的，离散程度大
B均值大的，离散程度大
C均值小的，离散程度小
D两组数据的离散程度相同
正确答案： C解析： 暂无解析 -
第13题：
直方图定量表示的主要特征值中的平均值(x)表示( )
A.数据的分散程度
B.数据范围的间隔
C.数据值的大小
D.数据的分布中心位置
正确答案：D
-
第14题：
●小王求出了一批数据的均值和方差，则(4)。
(4)A．均值可作为这批数据的代表，方差体现了这批数据的离散程度
B．均值位于这批数据的正中，方差反映了这批数据的误差
C．均值左右两边的数据一样多，方差是两两数据之差的平方和
D．均值必是这批数据中的某一数，方差是离均值最远的数
正确答案：A
-
第15题：
一组数据的均值为65，方差为25，则离散系数（ ）。
答案：D解析： -
第16题：
已知随机变量X的观测数据分别为：32、45、77、28、59；Y的观测数据为：122、210、185、296、108。试比较两变量X、Y的均值代表性优劣。
正确答案:由样本参数的计算公式可得变量X的样本均值为48.2、均方差为20.2、变差系数为0.42，变量Y的均值为146.4、均方差为102.1、变差系数为0.70，由统计参数的性质可知，变差系数越小的其取值的离散程度就越小，均值的代表性就越好，因此，变量X的样本均值的代表性要优于变量Y的。 -
第17题：
在生产实践中，经常要观察数据的分散程度和数据的集中程度。如平均值X就是用来表示（）。
- A、数据的集中位置
- B、数据的分散程度
- C、位置居中的数
- D、全部样本中各观测值的平均值
- E、总体数据的平均值
正确答案:A,D -
第18题：
两组数据的均值不同，但标准差相等，则（）
- A、均值小的，离散程度大
- B、均值大的，离散程度大
- C、均值小的，离散程度小
- D、两组数据的离散程度相同
正确答案:A -
第19题：
若数据服从正态分布，则均值大小不受数据中的极端值影响。（）
正确答案:错误 -
第20题：
问答题已知随机变量X的观测数据分别为：32、45、77、28、59；Y的观测数据为：122、210、185、296、108。试比较两变量X、Y的均值代表性优劣。正确答案： 由样本参数的计算公式可得变量X的样本均值为48.2、均方差为20.2、变差系数为0.42，变量Y的均值为146.4、均方差为102.1、变差系数为0.70，由统计参数的性质可知，变差系数越小的其取值的离散程度就越小，均值的代表性就越好，因此，变量X的样本均值的代表性要优于变量Y的。解析： 暂无解析 -
第21题：
单选题某同学由x与y之间的一组数据求得两个变量间的线性回归方程为y=bx+a，已知：数据x的平均值为2，数据y的平均值为3，则（）A回归直线必过点（2，3）
B回归直线一定不过点（2，3）
C点（2，3）在回归直线上方
D点（2，3）在回归直线下方
正确答案： D解析： 暂无解析 -
第22题：
问答题设总体X～N(μ,σ2)，x1,x2,…xn为其样本，为样本均值,则____．正确答案：解析： -
第23题：
单选题如果监测数据样本量较小，而数据值变化幅度较大，则水质参数选取（）A监测数据的平均值
B监测数据的最大值
C平均值与最大值的均方根
D平均值与最大值的立方根
正确答案： B解析： 暂无解析