设有某产品一盒共10只,已知其中有3只次品。从盒中任取两次,每次任取1只,作不放回抽样,则连续两次抽到次品的概率为( )。 A. 1/15 B. 1/12 C. 2/9 D. 3/10
题目
A. 1/15 B. 1/12 C. 2/9 D. 3/10
相似考题
更多“设有某产品一盒共10只,已知其中有3只次品。从盒中任取两次,每次任取1只,作不放回抽样,则连续两次抽到次品的概率为( )。 ”相关问题
-
第1题:
一盒灯泡共50个,已知其中有2个次品,任取2个灯泡都是次品的概率为________。
A.1/50
B.1/2450
C.1/1225
D.1/245
正确答案:C
-
第2题:
若10个产品中有7个正品,3个次品:(1)不放回地每次从中任取一个,共取3次,求取到3个次品的概率;(2)每次从中任取一个,有放回地取3次,求取到3个次品的概率。参考答案:P=3/10×2/9×1/8=1/120
(2)P´=3/10×3/10×3/10=27/1000
分析:对于第一题,第一次取到次品的概率为3/10,第二次再取时次品只有二件了,故为2/9,由此而类推的第三次。对于第二题,由于不放回,故每次取到次品的概率都为3/10。 -
第3题:
10个产品中有7个正品,3个次品,按不放回抽样,抽取2个产品,求两次都取到次品的概率是A.2/15
B.3/10
C.2/9
D.1/15
参考答案:D
-
第4题:
已知甲、乙两箱中装有同种产品,其中甲箱中装有3件合格品和3件次品,乙箱中仅装有3件合格品.从甲箱中任取3件产品放入乙箱后,乙箱中次品件数的数学期望和从乙箱中任取一件产品是次品的概率分别为( )A.2/3,1/4
B.2/5,1/4
C.2/3,1/3
D.1/3,1/4答案:A解析:乙箱中可能的次品件数为0,1,2,3,分别求出其概率,再按定义求数学期望即可;而求从乙箱中任取一件产品是次品的概率,涉及到两次试验,是典型的用全概率公式的情形,第一次试验的各种可能结果(取到的次品数)就是要找的完备事件组.
①X的可能取值为0,1,2,3,X的概率分布为
-
第5题:
设50件产品中,45件是正品,5件是次品,从中任取3件,求其中至少有l件
是次品的概率(精确到0.01).答案:解析:
-
第6题:
甲箱中有5个正品,3个次品;乙箱中有4个正品,3个次品。从甲箱中任取3个产品放入乙箱,然后从乙箱中任取1个产品,则这个产品是正品的概率为( )。
A. 0. 176 B. 0. 2679 C. 0. 3342 D. 0. 5875答案:D解析:设B={从乙箱中取得正品},A1={从甲箱中取出3个正品},A2={从甲箱中取出2个正品1个次品},A3={从甲箱中取出1个正品2个次品},A4 ={从甲箱中取出3 个次品},显然A1、A2、A3、A4都是互斥的,所以B=B(A1 + A2+ A3+ A4)。

P(B A1) =7/10,P(B A2) =6/10,P(B A3) =5/10,P(B A4) =4/10;
故P(B) =P(BA1+BA2 + BA3+ BA4) =P(A1)P(B A1) +P(A2)P(B A2) +P(A3)P (B A3) +P(A4)P(B A4) = (10/56) x (7/10) + (30/56) x (6/10) + (15/56) x (5/ 10) + (1/56) x (4/10) =0.5875。 -
第7题:
甲乙丙厂生产产品所占的比重分别为60%,25%,15%,次品率分别为3%,5%,8%,求任取一件产品是次品的概率.答案:解析:
-
第8题:
10件产品有3件次品,7件正品,每次从中任取一件,取后不放回,求下列事件的概率:
(1)第三次取得次品;
(2)第三次才取得次品;
(3)已知前两次没有取到次品,第三次取得次品;(4)不超过三次取到次品.答案:解析:【解】设Ai={第i次取到次品}(i=1,2,3).
(1)
(2)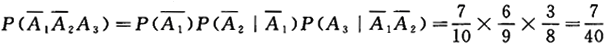 (试验还没有开始,计算前两次都取不到次品,且第三次取到次品的概率).
(试验还没有开始,计算前两次都取不到次品,且第三次取到次品的概率).
(3) (已知前两次已发生的结果,唯一不确定的就是第三次).
(已知前两次已发生的结果,唯一不确定的就是第三次).
(4)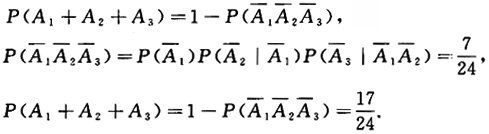
-
第9题:
一批产品共有10个正品和2个次品,任意抽取两次,每次抽一个,抽出后不再放回,则第二次抽出的是次品的概率为().
正确答案:2/5 -
第10题:
某工厂的次品率为5%,并且正品中有80%为一等品,如果从该厂的产品中任取一件来检验,那么检验结果是一等品的概率为19/25
正确答案:正确 -
第11题:
已知10支晶体管中有3个次品,现从中不放回的连续依次取出两支,则两次取出的晶体管都是次品的概率是()
正确答案:1/15 -
第12题:
问答题3.设在15个同类型的零件中有2个是次品,从中任取3次,每次取1个,取后不放回.以X表示取出的次品的个数,求X的分布律.正确答案:解析: -
第13题:
(本题满分10分) 设20件产品中有3件次品,从中任取两件,在已知其中有一件是次品的条件下,求另一件也是次品的概率.
正确答案:
-
第14题:
一批产品共50件,其中46件合格品,4件次品,从中任取3件,其中有次品的概率是多少? 次品不超过2件的概率是多少?参考答案:

-
第15题:
在一批N个产品中有M个次品,从这批产品中任取n个产品,其中含有m个次品的概率是( )。
 答案:B解析:这是个古典概率问题
答案:B解析:这是个古典概率问题 -
第16题:
设盒中有10个灯泡,其中次品3个,每次不放回地任取1个且任取两次.求
(1)第二次取到的也是正品的概率;(2)两次取到的都是正品的概率;
(3)第二次取到的是正品的概率.答案:解析:
-
第17题:
2012年3月15曰,某儿童玩具生产厂在对儿童玩具车的36件产品进行检验时,发现有4件次品,今从这36件产品中任取3件。
没有次品的概率为( )。
A. 0.0001
B. 0.0269
C. 0.2778
D. 0.6947答案:D解析: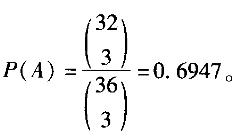
-
第18题:
已知一个箱子中装有12件产品,其中有2件次品。若从箱子中随机抽取2件产品进行检验,则恰好抽到1件次品的概率是: 答案:B解析:第一步,本题考查概率问题。
答案:B解析:第一步,本题考查概率问题。
第二步,一个箱子装有12件产品,其中2件次品,则有12-2=10(件)非次品,随机抽出2件产品,恰好有1件次品,则抽出的另1件为非次品。那么抽出的2件产品恰好是1件次品1件非次品有
故抽取2件产品恰好有1件次品的概率为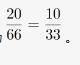
-
第19题:
已知甲、乙两箱中装有同种产品,其中甲箱中装有3件合格品和3件次品,乙箱中仅装有3件合格品.从甲箱中任取3件产品放入乙箱后,求:
(1)乙箱中次品件数X的数学期望;
(2)从乙箱中任取一件产品是次品的概率.答案:解析:
-
第20题:
一批产品有10个正品2个次品,任意抽取两次,每次取一个,抽取后不放回,求第二次抽取次品的概率.答案:解析:【解】令A1={第一次抽取正品},A2={第一次抽取次品},B={第二次抽取次品},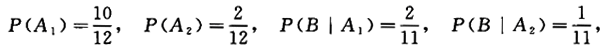
由全概率公式得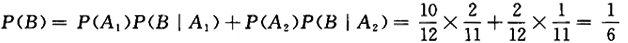
注解 不放回抽取的情况下,第一次抽取的结果未知时,第二次抽取某种产品的概率与第一次抽取的概率相同。 -
第21题:
已知10个灯泡中有3个次品,现从中任取4个,问取出的4个灯泡中至少有1个次品的概率是()
正确答案:5/6 -
第22题:
如果100件产品中,有10件次品,不放回地从中接连抽取两次,每次抽取一件,则第二次取到次品的概率是1/10
正确答案:正确 -
第23题:
从数字1,2,…,10中有放回地任取4个数字,则数字10恰好出现两次的概率为()
正确答案:0.0486 -
第24题:
问答题7.10个产品中有7件正品、3件次品. (1)不放回地每次从中任取一件,共取3次,求取到3件次品的概率; (2)每次从中任取一件,有放回地取3次,求取到3件次品的概率.正确答案:解析:
