从中任取两球都是白球的概率为________。A．5/12B．7/12C．5/33D．7/22

题目

从中任取两球都是白球的概率为________。

A．5/12

B．7/12

C．5/33

D．7/22

相似考题

1.袋中有球12个,2白10黑,今从中取4个,试求(1)恰有一个白球的概率(2)至少有一个白球的概率。

2.从中任取两球都是黑球的概率为________。A．5/12B．7/12C．5/33D．7/22

3.在一个盒子里装有均匀的已编有不同号码的五个白球和七个黑球,则从中任取一球是黑球的概率为________。A．5/12B．7/12C．5/33D．7/22

4.从中任取一球是白球的概率为________。A．5/12B．7/12C．5/33D．7/22

更多“从中任取两球都是白球的概率为________。A．5/12B．7/12C．5/33D．7/22”相关问题

  • 第1题：

    从中任取两球都是黑球的概率为( )。

    A．5/33

    B．7/22

    C．5/12

    D．7/12


    正确答案：B
    解析：

  • 第2题：

    从中任取一球是白球的概率为( )。

    A．5/33

    B．7/22

    C．5/12

    D．7/12


    正确答案：C
    解析：盒中共12个球，任取一个有12种取法，而取到白球有5种可能。所以任取一球是白球的概率为5/12。

  • 第3题：

    袋中有5个白球和3个黑球，从中任取两球，则取得的两球颜色相同的概率为13/28。()


    正确答案:对

  • 第4题：

    在一个盒子里装有均匀的已编有不同号码的五个白球和七个黑球，则：

    从中任取一球是黑球的概率为( )。

    A．5/33

    B．7/22

    C．5/12

    D．7/12


    正确答案：D
    解析：盒中共12个球，任取一个有12种取法，而取到黑球有7种可能。所以任取一球是黑球的概率为7/12。

  • 第5题：

    一袋中有5个乒乓球，其中4个白球，1个红球，从中任取2个球的不可能事件是（）

    A.｛2个球都是白球｝
    B.｛2个球都是红球｝
    C.｛2个球中至少有1个白球｝
    D.｛2个球中至少有1个红球｝

    答案：B
    解析：
    袋中只有1个红球，从中任取2个球都是红球是不可能发生的．

  • 第6题：

    袋中有8个乒乓球，其中5个白色球，3个黄色球，一次从中任取2个乒乓球，
    则取出的2个球均为白色球的概率为()．

    A.5/8
    B.5/14
    C.5/36
    D.5/56

    答案：B
    解析：

  • 第7题：

    袋中有8个乒乓球，其中5个白色球，3个黄色球，从中一次任取2个乒乓球，则取出的2个球均为白色球的概率为《》（ ）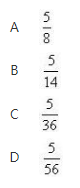


    答案：B
    解析：

  • 第8题：

    在一个盒子里装有均匀的已编有不同号码的五个白球和七个黑球，则：
    从中任取一球是白球的概率为（ ）。
    A. 5/33 B. 7/22 C. 5/12 D. 7/12


    答案：C
    解析：
    盒中共12个球，任取一个有12种取法，而取到白球有5种可能。所以任取一球是白球的概率为5/12。

  • 第9题：

    袋中有4个白球2个黑球，今从中任取3个球，则至少一个黑球的概率为（）

    • A、4/5
    • B、1
    • C、1/5
    • D、1/3

    正确答案:A

  • 第10题：

    一袋中有6个白球，4个红球，任取两球都是白球的概率是多少？（）

    • A、1/2
    • B、1/3
    • C、1/4
    • D、1/6

    正确答案:B

  • 第11题：

    单选题
    从中任取一球是白球的概率为（　　）。
    A

    5/33

    B

    7/22

    C

    5/12

    D

    7/12


    正确答案： D
    解析： 盒中共12个球，任取一个有12种取法，而取到白球有5种可能。所以任取一球是白球的概率为5/12。

  • 第12题：

    单选题
    袋中有5个白球 ，n个红球，从中任取一个恰为红球的概率为2/3，则n为(　　)
    A

    16  

    B

    10  

    C

    20   

    D

    18


    正确答案： B
    解析： 根据概率的定义：P=n/5+n=2/3

  • 第13题：

    从甲袋内摸出一个白球的概率是1/3,从乙袋内摸出一个白球的概率是1/2,从两个袋内各摸出一个球,那么________等于1/6。

    A．2个球都是白球的概率

    B．2个球都不是白球的概率

    C．2个球不都是白球的概率

    D．2个球中恰有1个白球的概率


    正确答案：A
    解析：从甲袋中摸出白球的概率为1/3,不是白球的概率为2/3:从乙袋中摸出白球的概率为1/2,摸出不是白球的概率也是1/2,从甲、乙袋中摸出白球的事件是相互独立的。因此,“两个都是白球的概率”为1/3×1/2=1/6;“两个都不是白球的概率”为2/3×1/2=1/3;“两个球中恰有1个白球的概率”为了1/3×1/2+2/3×1/2=1/2;“两个不都是白球的概率”为l-1/6=5/6(即减去两个都是白球的概率)。

  • 第14题：

    从装有2个红球和2个白球的袋内任取2球,那么互不相容的两个事件是________。

    A．“至少一个白球”与“都是白球”

    B．“至少一个白球”与“至少一个红球”

    C．“恰有一个白球”与“恰有两个白球”

    D．“至多一个白球”与“都是红球”


    正确答案：C
    解析：设“取到红球为1”,“取到白球为0”,则样本空间共有四个样本点,Ω={(0,0),(0,1),(1,0),(1,1)};“至少一个白球”={(0,0),(0,1),(1,0)};“都是白球”={(0,0)};“至多一个白球”=“至少一个红球”={(1,1),(0,1),(1,0)};“都是红球”={(1,1)};“恰有一个白球”={(0,1),(1,0)};“恰有两个白球”={(0,0)),所以答案A、B是相容事件,D是对立事件.C才是互不相容的事件。

  • 第15题：

    （3）一个口袋内装有除颜色外其他都相同的6个白球和4个红球，从中任意摸出2个，求：A、2个都是白球的概率；B、2个都是红球的概率；C、一个白球，一个红球的概率。


    正确答案：
              

  • 第16题：

    从中任取两球都是白球的概率为( )。

    A．5/33

    B．7/22

    C．5/12

    D．7/12


    正确答案：A
    解析：

  • 第17题：

    袋中装有大小相同的12个球，其中5个白球和7个黑球，从中任取3个球，求
    这3个球中至少有1个黑球的概率．


    答案：
    解析：
    此题利用对立事件的概率计算较为简捷，

  • 第18题：

    一个口袋内有4个不同的红球，6个不同的白球.
    (1)从中任取4个球，红球的个数不比白球少的取法有多少种?
    (2)若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于7分的取法有多少种?


    答案：
    解析：
    解：(1)由题意知本题是一个分类计数问题.将取出4个球分成三类情况：取4个红

  • 第19题：

    在一个盒子里装有均匀的已编有不同号码的五个白球和七个黑球，则：
    从中任取两球都是黑球的概率为（ ）。
    A. 5/33 B. 7/22 C. 5/12 D. 7/12


    答案：B
    解析：

  • 第20题：

    在一个盒子里装有均匀的已编有不同号码的五个白球和七个黑球，则：
    从中任取一球是黑球的概率为（ ）。
    A. 5/33 B. 7/22 C. 5/12 D. 7/12


    答案：D
    解析：
    盒中共12个球，任取一个有12种取法，而取到黑球有7种可能。所以任取一球是黑球的概率为7/12。

  • 第21题：

    一袋中有6个白球，4个红球，任取两球都是白球的概率是（）

    • A、1/2
    • B、1/3
    • C、1/4
    • D、1/6

    正确答案:B

  • 第22题：

    单选题
    从中任取一球是黑球的概率为（　　）。
    A

    5/33

    B

    7/22

    C

    5/12

    D

    7/12


    正确答案： D
    解析： 盒中共12个球，任取一个有12种取法，而取到黑球有7种可能。所以任取一球是黑球的概率为7/12。

  • 第23题：

    单选题
    一只盒子中有红球m个，白球10个，黑球n个，每个球除颜色外其他都相同，从中任取一个球，取得白球的概率与不是白球的概率相同，那么m与n的关系是（　　）．
    A

    m＝4，n＝6

    B

    m＝5，n＝5

    C

    m＋n＝5

    D

    m＋n＝10


    正确答案： B
    解析：
    因为从中任取一个球，取得白球的概率与不是白球的概率相同．所以白球的个数与不是白球的球的个数相等，所以m＋n＝10．

相关内容