听力原文：[*]当a=0.05时，因子A对试验结果的影响是( )。A．不显著B．显著C．不能确定 附：F0.90 (2，2)＝9.0；F0.25 (2，2)＝19.0；F0.975 (2，2)＝39.60

题目

听力原文：[*]

当a=0.05时，因子A对试验结果的影响是( )。

A．不显著

B．显著

C．不能确定 附：F0.90 (2，2)＝9.0；F0.25 (2，2)＝19.0；F0.975 (2，2)＝39.60

相似考题

1.听力原文：FA＞F0.95＞F0.90，故选项C也是正确的。在单因子试验中，因子A有3个水平，已知FA＞F0.95(2，4)，则下述结论正确的是( )。A．在a＝0.05上显著B．在a＝0.025上显著C．在a＝0.10上显著D．无法判定E．以上都不正确

2.当a=0．05时，用相关系数法检验回归方程中x对Y的影响是（ ）。A.不显著B.显著C.不能确定 附：r0．98(12)=0．457；r0.975(12)=0．532；0.975(13)=0．514。

3.当a=0．05时，因子A对试验结果的影响是（ ）。A.不显著B.显著C.不能确定D.其他 附：F0．90(2，2)=9．0；F0．95(2，2)=19．0；F0．975(2，2)=39．60

4.当a＝0.05时，用相关系数法检验回归方程中x对y的影响是( )。A．不显著B．显著C．不能确定 附：r0.98(12)＝0.457；r0.975(12)＝0.532；r0.97 (13)＝0.514

参考答案和解析
正确答案：B
解析：为了研究某种商品年需求量(公斤)和该商品价格(元)之间的关系，以家庭为单位，经随机抽样10个家庭调查获得一组数据，计算得到：∑X=30，∑Y=20，Lxx=-6，Lxy=8，Lyy=7.5[*]F1-0.05(1，8)＝5.32U0.975=1.96
更多“听力原文:[*] 当a=0.05时,因子A对试验结果的影响是()。A.不显著B.显著C.不能确定 附:F0.90 (2,2)= ”相关问题

  • 第1题：

    在一个用L9(34)安排的正交设计中，表头设计与各列平方和如表2.3-5所示，从F分布表查得F0.90(2，2)=9.0，F0.95(2，2)=19.0，则有( )。

    A．Se=S4

    B．三个因子都是显著的

    C．在显著性水平0.1上因子A是显著的

    D．在显著性水平0.05上因子B是显著的

    E．在显著性水平0.05上因子C是显著的


    正确答案：ACD
    解析：由于第四列为空白列，所以Se=S4，三个因子作检验的F比分别为。由于9.0FA19.0，FB＞19.0，FC9.0，所以因子A在显著性水平0.1上是显著的，因子B在显著性水平0.05上是显著的。对于显著性水平0.1和0.5，因子C都是不显著的。

  • 第2题：

    正交试验设计数据分析的结果表明，因子A与因子B的交互作用对某零件耐压性有显著的影响，这意味着（ ）。
    A.因子A或因子B对耐压性有显著的影响B.因子A和因子B都是影响零件耐压性的显著因素
    C.因子A与B的不同水平组合对耐压性有显著影响
    D.当因子A、B均处于最优水平时，耐压性一定达到最优
    E.单独来看，因子A和B可能对耐压性都没有显著影响


    答案：C,E
    解析：
    在多因子试验中，除了单个因子对指标有影响外，有时两个因子不同水平的搭配对指标也会产生影响，这种影响如果存在就称为因子A与B的交互作用。一个因子的水平好坏或好坏的程度受另一因子水平制约的情况，称为因子A与B的交互作用，用AXB表示。单独来看，因子A和B可能对耐压性都没有显著影响，但是相互作用就会对耐压性有显著影响。

  • 第3题：

    在一个用L9(34)的正交试验中，各列的偏差平方和如表所示，给定F0.90(2,2)=9.0、F0.95(2, 2) = 19.0，下列与本数据结果有关的正确项有（ ）。

    A. A、B、C 为显著（a =0.05）
    B. A 因子（a =0. 10）显著
    C. B 因子（a =0.05）显著
    D. Se≠S4
    E. C因子(a= 0.05)不显著


    答案：B,C,E
    解析：
    由题意知，因子水平数均为3，SA= 1320, SB=5110, SC=468，Se=88，其中，Se=S4； fA=fB=fc=2，fe=2，则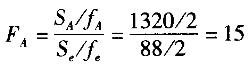，同理可得FB=58.07，FC =5.32，因为F0.90(2,2)A0.95(2,2)；FB>F0.95(2,2)； FC0.95(2,2)，所以A因子(a=0. 10)显著，B因子（a =0.05）显著，C因子都不显著。

  • 第4题：

    在一个用L9(34)的正交试验中，各列的偏差平方和如表2.3-6所示，给定F0.90(2，2) =9.0、F0.95(2，2)=19.0，下列与本数据结果有关的正确项有( )。

    A．A、B、C为显著(α=0.05)

    B．A因子(α=0.10)显著

    C．B因子(α=0.05)显著

    D．S4≠Se

    E．C因子(α=0.05)不显著


    正确答案：BCE
    解析：由题意，因子水平数均为3，SA=1320，SB=5110，SC=468，Se=88，其中，S4=Se；fA=fB=fC=2，fe=2。则，同理可得FB=58.07，FC=5.32，因为F0.95(2，2)FAF0.95(2，2)；FB＞F0.95(2，2)；FCF0.90(2，2)，所以A因子(α=0.10)显著，B因子(α=0.05)显著，C因子都不显著。

  • 第5题：

    在一个用L9(34)安排的正交设计中，表头设计与各列平方和如表所示，从F分布表查得 F0.90(2, 2) =9.0, F0.95(2,2) =19.0，则有（ ）。

    A. Se=S4
    B.三个因子都是显著的
    C.在显著性水平0. 1上因子A是显著的
    D.在显著性水平0. 05上因子B是显著的
    E.在显著性水平0. 05上因子C是显著的


    答案：A,C,D
    解析：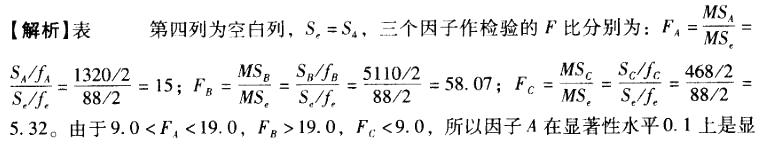

    著的，因子B在显著性水平0.05上是显著的。对于显著性水平0. 1和0.5，因子C都是不显著的。

相关内容