某六西格玛团队通过界定项目过程的输出，明确了缺陷的机会是甲、乙、丙。经过调查统计2个月的数据，结果在抽取的200个产品中，发现缺陷甲的个数为2、乙的个数为3、丙的个数为1，则该过程的DPMO为（ ）。 A. 10 000 B. 30 000 C. 60 000 D. 600

题目
某六西格玛团队通过界定项目过程的输出，明确了缺陷的机会是甲、乙、丙。经过调查统计2个月的数据，结果在抽取的200个产品中，发现缺陷甲的个数为2、乙的个数为3、丙的个数为1，则该过程的DPMO为（ ）。
A. 10 000
B. 30 000
C. 60 000
D. 600

相似考题

1.已知甲的12%为13，乙的13%为14，丙的14%Y；J15，丁的15%为16，则甲、乙、丙、丁四个数中最大的数是（ ）。A．甲B．乙C．丙D．丁

2.某六西格玛团队界定某项目过程的输出时，明确某产品可能出现的缺陷有甲、乙、丙三种。经过调查统计2个月的数据，结果是在抽样的200个产品中，发现甲种的缺陷个数为2、乙种的个数为3、丙种的个数为1，则DPMO为( )。A．600B．10000C．30000D．60000

3.有甲、乙、丙、丁四个数，已知甲的8%为9，乙的9%为10，丙的10%为11，丁的11%为12，则甲、乙、丙、丁四个数中最小的数是( )。A．甲B．乙C．丙D．丁

4.有甲、乙、丙、丁四个数，已知甲的8%是9，乙的9%是10，丙的10%是11，丁的11%是12，甲、乙、丙、丁四个数中最小的数是：A.甲 B.乙 C.丙 D.丁

更多“某六西格玛团队通过界定项目过程的输出，明确了缺陷的机会是甲、乙、丙。经过调查统计2个月的数据，结果在抽取的200个产品中，发现缺陷甲的个数为2、乙的个数为3、丙的个数为1，则该过程的DPMO为（ ）。 ”相关问题

  • 第1题：

    甲、乙、丙、丁四个工人做了270个零件，如果甲多做10个，乙少做10个，丙做的个数乘2，丁做的个数除以2，那么四人做的零件数恰好相等。丙实际做多少个？（ ）

    A．30

    B．45

    C．52

    D 63


    正确答案：A
    设四人做的零件数恰好相等的数为X，则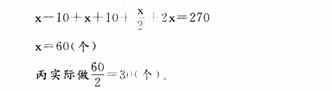

  • 第2题：

    在一棵度为4的树中，度为4的结点个数为1，度为3的结点个数为2，度为2的结点个数为 2，则叶子结点个数为( )。

    A．8

    B．9

    C．10

    D．11


    正确答案：C
    解析：对一棵树，除了根结点外，其余每个结点入度都为1，因此树的度的和为结点数减1，设叶子结点数为x，则结点总数为(1+2+2+x)，度的和为x+4。同时所有结点中只有叶子结点的度为0，所以x+4=4*1+3*2+2*2，得到x=10。

  • 第3题：

    549是甲、乙、丙、丁4个数的和。如果甲数加上2，乙数减少2，丙数乘以2，丁数除以2以后，则4个数相等。求4个数各是多少？（ ）

    A．120，124，61，244

    B．121，125，60，243

    C．120，123，60，246

    D．122，124，60，243


    正确答案：A

    从题干中首先可得出，丙数最小。由于丙数乘以2和丁数除以2相等，也就是丙数的2倍和丁数的一半相等，即丁数相当于丙数的4倍。乙减2之后是丙的2倍，甲加上2之后也是丙的2倍。根据这些倍数关系，可以先求出丙数，再分别求出其他各数。①丙数是：(549+2-2)÷(2+2+l+4)＝549÷9＝61，②甲数是：61×2-2＝120，③乙数是：61×2+2＝124，④丁数是：61×4＝244，所以，甲、乙、丙、丁分别是120、124、61、244。故选A。

  • 第4题：

    某六西格玛项目团队，需要了解以下问题：
    项目界定和测量时，需要确定缺陷机会和DPMO及西格玛水平。统计其过程输出，有10个变量都可能出现缺陷，在抽取的10 000件样本产品中，缺陷总数为40，项目过程输出的缺陷机会数为（ ）。
    A. 10 B. 4
    C. 3 D. 7


    答案：A
    解析：

  • 第5题：

    已知有甲、乙、丙、丁四个数，甲、乙之和大于丙、丁之和，甲、丁之和大于乙、丙之和，乙、丁之和大于甲、丙之和。根根据以上请判断这四个数谁最小？（）
    A 甲最小
    B 丙最小
    C 乙最小
    D 丁最小


    答案：B
    解析：
    第一步：整理题干信息。
    （1）甲＋乙>丙＋丁；（2）甲＋丁>乙＋丙；（3）乙＋丁>甲＋丙。
    第二步：根据信息整合。
    将不等式相加，同方向的不等号不变，（1）+（2）可得甲>丙，（2）+（3）可得丁>丙，（1）+（3）可得乙>丙，综合三个结果可知丙最小。
    故正确答案为B。

  • 第6题：

    甲从1、2、3中抽取一个数，记为a；乙从1、2、3、4中抽取一个数，记为b，规定当a大于b或者a+1小于b时甲获胜，则甲取胜的概率为（ ）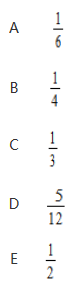


    答案：E
    解析：
    穷举法：满足a大于b的有（2,1）（3,1）（3,2）；满足a+1小于b的有（1,3）（1,4）（2,4）；共六组，因此概率为3/6=1/2

  • 第7题：

    已知甲的12%为13，乙的13%为14，丙的14%为15，丁的15%为16，则甲、乙、丙、丁四个数中最大的数是（）。

    • A、甲
    • B、乙
    • C、丙
    • D、丁

    正确答案:A

  • 第8题：

    单选题
    已知有甲、乙、丙、丁四个数，甲乙之和大于丙丁之和，甲丁之和大于乙丙之和，乙丁之和大于甲丙之和。根据以上请判断这四个数谁最小？（　　）
    A

    甲最小

    B

    丙最小

    C

    乙最小

    D

    丁最小


    正确答案： B
    解析：
    由题可知：①甲＋乙＞丙＋丁；②甲＋丁＞乙＋丙；③乙＋丁＞甲＋丙。由①＋②可推知甲＞丙，由①＋③可推知乙＞丙，由②＋③可推知丁＞丙，即丙最小。因此B项正确。

  • 第9题：

    已知甲的13%为 14，乙的 14%为 15，丙的 15%为 16，丁的16%为17，则甲、乙、丙、

    丁四个数中最大的数是( )。

    A.甲

    B.乙

    C.丙

    D.丁


    正确答案：A

  • 第10题：

    在一棵度为4的树中，度为4的结点个数为2，度为3的结点个数为1，度为2的结点个数为3，则叶子结点个数为 ______。


    正确答案：12
    12 解析：对一棵树，除了根结点外，其余每个结点入度都为1，因此树的度的和为结点数减1，设叶子结点数为x，则结点总数为(x+2+1+3)，度的和为x+5。同时所有结点中只有叶子结点的度为0，所以x+5=4*2+3*1+2*3，得到x=12。

  • 第11题：

    某六西格玛团队界定某项目过程的输出时，明确某产品可能出现的缺陷有甲、乙、丙三种。经过调查统计2个月的数据，结果是在抽样的200个产品中，发现甲种的缺陷个数为2、乙种的个数为3、丙种的个数为1，则DPMO为（ ）。
    A. 600 B. 10000 C. 30000 D. 60000


    答案：B
    解析：
    该产品总的缺陷数为：2+3+1=6,机会数为3,则：

    = (6x 106)/(200 x 3) = 10000。

  • 第12题：

    有甲、乙、丙、丁、四个数字，已知甲的8%为9，乙的9%为10，丙的10%为11，丁的11%为12， 则min(甲、乙、丙、丁)是：


    A. 甲
    B. 乙
    C. 丙
    D. 丁

    答案：D
    解析：
    解题指导： 根据题干，甲=9×100÷8=（1+1÷8）×100，乙=10×100÷9=（1+1÷9）×100，丙=11×100÷10=（1+1÷10）×100，丁=12×100÷11=（1+1÷11）×100。故答案为D。

  • 第13题：

    某流水施工组织成倍节拍流水，施工段数为6，甲、乙、丙三个施工过程的流水节拍为2d、2d和4d，其中乙、丙施工过程的间隔时间为2d，则总工期为（　　）d。

    A．14
    B．18
    C．20
    D．26

    答案：C
    解析：
    根据成倍节拍流水施工组织方法：流水步距=min{2，2，4}=2d，甲、乙、丙的施工队伍数分别为2／2=1，2／2=1，4／2=2，总的施工队数为1+1+2=4，则总工期T=（m+n-1）K+∑Z=（6+4-1）×2+2=20d。

  • 第14题：

    某六西格玛团队，界定项目过程的输出时，明确缺陷的机会是甲、乙、丙，经过调查统计2个月的数据，结果是在抽样200个产品中，发现缺陷甲的个数为2、乙的个数为3、丙的个数为1，则DPMO为（）

    • A、60000
    • B、30000
    • C、10000
    • D、600

    正确答案:C

  • 第15题：

    单选题
    某六西格玛团队，界定项目过程的输出时，明确缺陷的机会是甲、乙、丙，经过调查统计2个月的数据，结果是在抽样200个产品中，发现缺陷甲的个数为2、乙的个数为3、丙的个数为1，则DPMO为（）
    A

    60000

    B

    30000

    C

    10000

    D

    600


    正确答案： D
    解析： 暂无解析

相关内容