设随机变量X1与X2相互独立,它们的均值分别为3与4,方差分别为1与2,则Y=4X1 -2X2的均值与方差分别为( )。 A. E(Y) =4 B. E(Y) =20 C. Var(Y) = 8 D. Var(Y) = 14 E. Var(Y) =24
题目
设随机变量X1与X2相互独立,它们的均值分别为3与4,方差分别为1与2,则Y=4X1 -2X2的均值与方差分别为( )。
A. E(Y) =4 B. E(Y) =20 C. Var(Y) = 8 D. Var(Y) = 14
E. Var(Y) =24
A. E(Y) =4 B. E(Y) =20 C. Var(Y) = 8 D. Var(Y) = 14
E. Var(Y) =24
相似考题
更多“设随机变量X1与X2相互独立,它们的均值分别为3与4,方差分别为1与2,则Y=4X1 -2X2的均值与方差分别为( )。 ”相关问题
-
第1题:
设随机变量X与Y相互独立,方差分别为6和3,则D(2X-Y)=( )。A.9
B.15
C.21
D.27答案:D解析:由X与Y相互独立,D(2X-Y)=4DX+DY=27。 -
第2题:
设两个相互独立的随机变量X和Y的方差分别为4和2,则随机变量3X-2Y的方差是( )。A.8
B.16
C.28
D.44答案:D解析:直接利用相互独立随机变量方差公式进行计算即可。D(3X-2Y)=32D(X)+22D(Y)=9×4+4×2=44 -
第3题:
随机变量X与Y相互独立,X的均值为5,标准差也为5,Y的均值为9,方差为16,则V=2X+3Y的均值与方差分别为( )。A. 22; 164 B. 22; 244 C. 37; 164 D. 37; 244答案:D解析:由题意,E(X) =5, Var(X) =25,E(Y)=9, Var(Y) =16;则E(V) =E(2X + 3Y)=2E(X) +3E(Y) =2 x5 +3 x9 =37,Var(2X+3Y) =4Var(X) +9Var(Y) =4 x25 + 9 x 16 =100 +144 =244。 -
第4题:
设随机变量X与Y相互独立,且X的标准差为3,Y的方差为4,则X-2Y的方差为( )。
A.7
B.13
C.17
D.25答案:D解析:。Var(X-2Y)=Var(X)+ 4Var(Y)= 9 + 16 = 25。 -
第5题:
设总体X,Y相互独立且都服从N(μ,σ^2)分布,(X1,X2,…,Xn)与(Y1,Y1,…,yn)分别为来自总体X,Y的简单随机样本,证明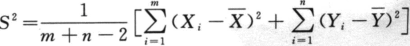 :为参数σ^2的无偏估计量,答案:解析:
:为参数σ^2的无偏估计量,答案:解析: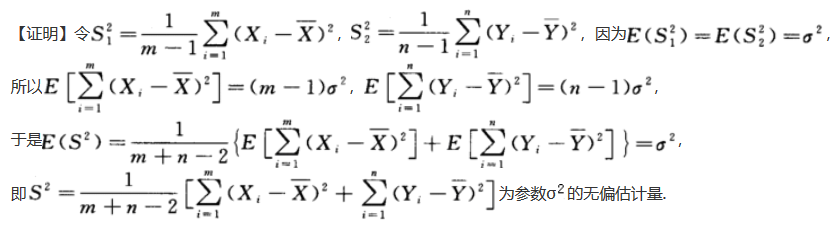
-
第6题:
设两个互相独立的随机变量X和Y的方差分别为2和4,则随机变量2X-3Y的方差;是( )。A.-28
B.-8
C.8
D.44答案:D解析:D(2X-3Y)=D(2X)+D(3Y)=4D(X)+9D(Y)=44 -
第7题:
设有两个样本,样本A:x1, X2 ,…,Xn ;样本B:x1+d,x2+d,x···,xn+d(d为常数)又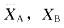 分别为它们的样本均值,S2A,S2B分别为它们的样本方差,则 ( )。
分别为它们的样本均值,S2A,S2B分别为它们的样本方差,则 ( )。
 答案:C,D解析:
答案:C,D解析: -
第8题:
设随机变量X与Y相互独立,方差分别为6和3,则D(2X-Y)=()。
- A、9
- B、15
- C、21
- D、27
正确答案:D -
第9题:
设随机变量X和Y的数学期望分别为-2和2,方差分别为1和4,而相关系数为-0.5,则根据切比雪夫不等式P{|X+Y|≥6}≤()。
正确答案:1/12 -
第10题:
单选题随机变量X与Y相互独立,X的均值为5,标准差也为5,Y的均值为9,方差为16,则V=2X+3Y的均值与方差分别为( )。A22;164
B22;244
C37;164
D37;244
正确答案: D解析:
由题意,E(X)=5,Var(X)=25,E(Y)=9,Var(Y)=16;则E(V)=E(2X+3Y)=2E(X)+3E(Y)=2×5+3×9=37,Var(2X+3Y)=4Var(X)+9Var(Y)=4×25+9×16=100+144=244。 -
第11题:
单选题设随机变量X1、X2相互独立,它们的分布列分别为:A0.27
B0.20
C0.17
D0.07
E0.02
正确答案: B解析: 利用两项和卷积公式计算得:
PS(2)=P(X1=0,X2=2)+P(X1=1,X2=1)+P(X1=2,X2=0)
=0.5×0.2+0.3×0.3+0.2×0.4
=0.27。 -
第12题:
多选题设随机变量X1与X2相互独立,它们的均值分别为3与4,方差分别为1与2,则y=4X1αX2的均值与方差分别为( )。AE(y)=4
BE(y)=20
CVar(y)=14
DVar(y)=24
EVar(y)=15
正确答案: B,E解析: E(y)=4×3-2×4=4Var(y)=16×1+4×2=24
-
第13题:
设F1(x)与F2(x)分别为随机变量X1与X2的分布函数。为使F(x)=aF1(x)-bF2(x)成为某一随机变量的分布函数,则a与b分别是: 答案:A解析:
答案:A解析:
-
第14题:
设总体X~N(μ,σ^2),X1,X2,…,Xn为总体X的简单随机样本,X与S^2分别为样本均值与样本方差,则(). 答案:A解析:
答案:A解析: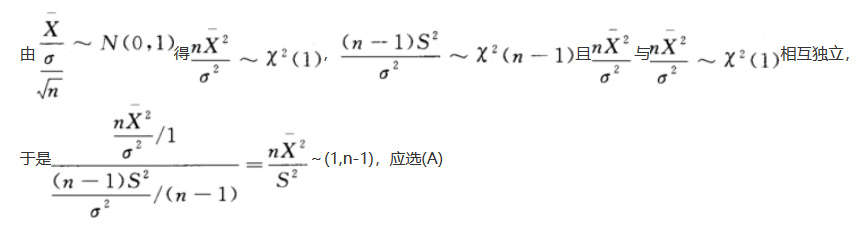
-
第15题:
设随机变量X1和X2相互独立,它们的均值分别为3与4,方差分别为1与2,则 Y = 4X1+2X2的均值与方差分别为( )。
A. E (Y) =4 B. E (Y) =20
C.Var (Y) =14 D.Var (Y) =24
E.Var (Y) =15答案:B,D解析:。E (Y) =E(4X1+ 2X2) =4×3 + 2×4 = 20; Var (Y) =Var (4X1 + 2X2 ) =42 × 1 + 22 ×2 = 24。 -
第16题:
设随机变量X1,X2,…,Xn相互独立且在[0,na]上服从均匀分布,令U=max{X1,X2,…,Xn},求U的数学期望与方差.答案:解析:
-
第17题:
已知X1、X2、X3的平均值为3,方差为2,则X1+1、X2+1、X3+1的平均值和方差分别为( )和( )。A、4和2
B、3和2
C、3和3
D、4和3答案:A解析:期望值衡量的是X的平均水平,因为每个X1、X2、X3都增加1,所以它们的平均值也是增加1;方差衡量的是这组数据的波动性,因为每个数值增加的数额相同,所以波动性没有发生变化,因此方差还是2。 -
第18题:
设随机变量X与Y相互独立,方差分别为6和3,则D(2X-Y)=( )。
A. 9 B. 15 C. 21 D. 27答案:D解析:提示:利用方差的性质。 -
第19题:
设两个相互独立的随机变量X和Y的方差分别为4和2,则随机变量3X-2Y的方差是()
- A、8
- B、16
- C、28
- D、44
正确答案:D -
第20题:
设随机变量X与Y相互独立,它们分别服从参数λ=2的泊松分布与指数分布.记Z=X-2Y,则随机变量Z的数学期望与方差分别等于().
- A、1,3
- B、-2,4
- C、1,4
- D、-2,6
正确答案:A -
第21题:
单选题随机变量X的平均值为5,标准差也为5,随机变量Y的均值为9,方差为l6,则V=2X+3Y的均值与方差为( )。A37,164
B37,244
C22,164
D22,244
正确答案: D解析: x的平均值为5也就是均值为5,其标准差为5则其方差为25,则E(2x+3y)=2E(x)+3E(y)=2×5+3×9=37 Vat(2x+3y)=4 Var(x)+9 Vat(y)=4×25+9×16=100+144=244
-
第22题:
单选题设两个相互独立的随机变量X和Y的方差分别为4和2,则随机变量3X-2Y的方差是( )。A8
B16
C28
D44
正确答案: B解析:
D(3X-2Y)=32D(X)+22D(Y)=9×4+4×2=44。 -
第23题:
多选题设随机变量X1与X2相互独立,它们的均值分别为3与4,方差分别为1与2,则Y=4X1-2X2的均值与方差分别为( )。AE(Y)=4
BE(Y)=20
CVar(Y)=8
DVar(Y)=14
EVar(Y)=24
正确答案: B,A解析:
E(Y)=E(4X1-2X2)=4E(X1)-2E(X2)=4×3-2×4=4;
Var(Y)=Var(4X1-2X2)=42Var(X1)+(-2)2Var(X2)=16×1+4×2=24。
