θ是总体的一个待估参数,θL,θU是其对于给定a的1-a的置信下限与置信上限。则1-a置信区间的含义是( )。 A.所构造的随机区间[θL,θU]覆盖(盖住)未知参数θ的概率为1 - a B.由于这个随机区间随样本观测值的不同而不同,它有时覆盖住了参数θ,有时则没有覆盖参数θ C.用这种方法做区间估计时,不能覆盖参数θ的机率相当小 D.如果P(θL) =P(θ>θU)=a/2,则称这种置信区间为等尾置信区间 E.正态总体参数的置信区间是等尾置信区间,而比例p的置信区间不是等尾置信区间
题目
A.所构造的随机区间[θL,θU]覆盖(盖住)未知参数θ的概率为1 - a
B.由于这个随机区间随样本观测值的不同而不同,它有时覆盖住了参数θ,有时则没有覆盖参数θ
C.用这种方法做区间估计时,不能覆盖参数θ的机率相当小
D.如果P(θL) =P(θ>θU)=a/2,则称这种置信区间为等尾置信区间
E.正态总体参数的置信区间是等尾置信区间,而比例p的置信区间不是等尾置信区间
相似考题
更多“θ是总体的一个待估参数,θL,θU是其对于给定a的1-a的置信下限与置信上限。则1-a置信区间的含义是( )。 ”相关问题
-
第1题:
设θ是总体的一个待估参数,现从总体中抽取容量为n的一个样本,从中得到参数θ的一个置
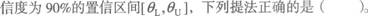
A.
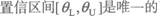
B.100个置信区间中约有90个区间能包含真值θ
C.100个置信区间中约有5个区间能包含真值0
D.
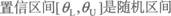
E.100个置信区间中约有90个区间不能包含真值θ
正确答案:BD
置信度为95%的区间的概念是:构造的随机区间有95%能覆盖住θ。 -
第2题:
已知总体服从正态分布,且总体标准差σ,从总体中抽取样本容量为n的产品,测得其样本均值为x,在置信水平为1-a=95%下,总体均值的置信区间为( )
 正确答案:A
正确答案:A
-
第3题:
关于置信度为95%的置信区间的说法正确的是( )。
A.置信区间为[463.63,502.37]
B.置信区间为[494.90,501.10]
C.置信区间是以X为中心,宽度是[*]
D.对于较大的α,置信区间则较窄;对于较小的α,置信区间则较宽
正确答案:BCD
解析:从上下限计算公式中:可以看出,置信区间是以为中心,宽度是。当。较大时,Zα/2较小,从而置信区间较窄;当α较小时,Zα/2较大,从而置信区间较宽。 -
第4题:
总体X~N(μ,5^2),则总体参数μ的置信度为1-a的置信区间的长度().A.与α无关
B.随α的增加而增加
C.随α的增大而减少
D.与α有关但与α的增减性无关答案:C解析:总体方差已知,参数卢的置信度为1-α的置信区间为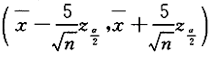 ,其中n为样本容量,长度
,其中n为样本容量,长度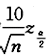 ,因为α越小,则
,因为α越小,则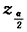 越大,所以置信区间的长度随α增大而减少,选(C).
越大,所以置信区间的长度随α增大而减少,选(C). -
第5题:
设总体X~N(u,σ2),u与σ2均未知,x1,x2,...,x9为其样本, 样本方差,则u的置信度为0. 9的置信区间是:
样本方差,则u的置信度为0. 9的置信区间是:
 答案:C解析:
答案:C解析:
-
第6题:
总体为正态分布,σ2未知,则总体均值的1-a置信区间是()。 答案:B解析:估计正态总体均值的置信区间,若σ未知,σ用其估计s代替,利用t分布,且是对称区间,故总体均值置信区间为
答案:B解析:估计正态总体均值的置信区间,若σ未知,σ用其估计s代替,利用t分布,且是对称区间,故总体均值置信区间为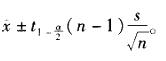
-
第7题:
在大样本条件下,若np≥5,且n(1-p)≥5,样本比例在置信水平(1-a)下的置信区间为( )。
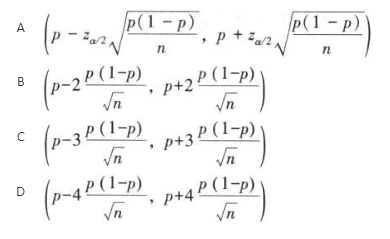 答案:A解析:
答案:A解析: -
第8题:
总体率(1-a)置信区间指()。
- A、求得的区间包含总体率的可能性为(1-A.
- B、计算样本率抽样误差的大小
- C、求得总体率的波动范围
- D、估计样本率的大小
- E、估计样本含量
正确答案:A -
第9题:
对总体参数进行区间估计,则下列结论正确的是()
- A、置信度越大,置信区间越长
- B、置信度越大,置信区间越短
- C、置信度越小,置信区间越长
- D、置信度大小与置信区间长度无关
正确答案:A -
第10题:
置信度1-α是指总体参数落在置信区间的概率是1-α。
正确答案:错误 -
第11题:
置信区间CI是随机的,总体参数是固定的。
正确答案:正确 -
第12题:
多选题设[θL,θU]是θ的置信水平为1-α的置信区间,则有( )。[2006年真题]Aα愈大,置信区间长度愈短
Bα愈大,置信区间长度愈长
Cα愈小,置信区间包含θ的概率愈大
Dα愈小,置信区间包含θ的概率愈小
E置信区间长度与α大小无关
正确答案: E,A解析:
1-α置信区间的含义是:所构造的随机区间[θL,θU]覆盖(盖住)未知参数θ的概率为1-α。α愈大,区间[θL,θU]盖住未知参数θ的概率越小,区间的长度越短;α愈小,区间[θL,θU]盖住未知参数θ的概率越大,置信区间的长度越长。 -
第13题:
小样本情况下,总体服从正态分布,总体方差未知,总体均值在置信水平(1-a)下的置信区间为( )
 正确答案:A
正确答案:A
-
第14题:
听力原文:构造的随机区间[θL;θU]是θ的置信水平为99%的置信区间,它的含义是指所构造的[θL,θU]区间覆盖住未知参数θ的概率为99%。
参数θ的一个置信度为99%的置信区间[θL,θU),则下列说法正确的是( )。
A.置信区间[θL,θU]是一个随机区间
B.在100个这样的置信区间中,约有1个区间包含真值θ
C.置信区间[θL,θU]不是随机区间
D.在100个这样的置信区间中,约有99个区间包含真值θ
E.以上说法都不正确
正确答案:AD
-
第15题:
正态总体标准差σ的1-a置信区间为( )。(μ未知)。
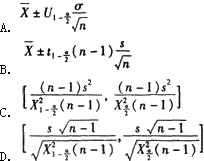 正确答案:D
正确答案:D
-
第16题:
设总体X~N(μ,σ^2),其中σ^2未知,^2s=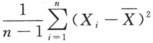 ,样本容量n,则参数μ的置信度为1-a的置信区间为().
,样本容量n,则参数μ的置信度为1-a的置信区间为().
 答案:D解析:因为σ^2未知,所以选用统计量
答案:D解析:因为σ^2未知,所以选用统计量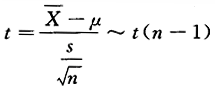 ,故μ的置信度为1-α的置信区间为
,故μ的置信度为1-α的置信区间为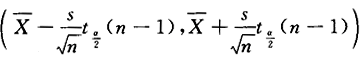 ,选(D).
,选(D). -
第17题:
设[θL, θU]是θ的置信水平为1-a的置信区间,则有( )。
A.a愈大,置信区间长度愈短 B.a愈大,置信区间长度愈长
C.a愈小,置信区间包含θ的概率愈大 D.a愈小,置信区间包含θ的概率愈小
E.置信区间长度与a大小无关答案:A,C解析:1-a置信区间的含义是:所构造的随机区间[θL, θU]覆盖(盖住)未知参数θ的概率为1-a。a愈大,区间[θL, θU]盖住未知参数θ的概率越小,区间的长度越短;a愈小,区间[θL, θU]盖住未知参数θ的概率越大,置信区间的长度越长。 -
第18题:
正态总体参数均值、方差、标准差的1-a置信区间为()。 答案:A,B,D,E解析:
答案:A,B,D,E解析:

-
第19题:
当σ2已知时,总体均值μ在1-a置信水平下的置信区间为( )。
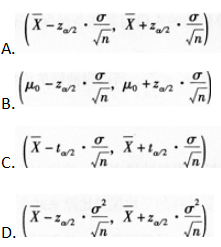 答案:A解析:
答案:A解析: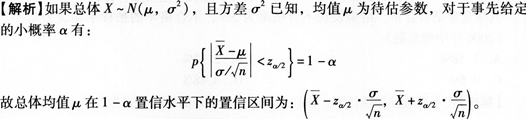
-
第20题:
关于参数估计的正确说法是()。
- A、对母体参数的点估计使用一个统计的单一值去估计一个位置参数的数值。
- B、在给定置信度(1-α)的情况下,对未知参数的置信上限和置信下限做出估计的方法是双侧区间估计,又称双边估计。
- C、在给定置信度(1-α)的情况下,只对未知数的置信下限或置信上限做出估计的方法是单侧区间估计,又称单边估计。
- D、以上都对
正确答案:D -
第21题:
置信水平(1-α)是()
- A、置信区间估计正确的概率
- B、置信区间估计错误的概率
- C、保证置信区间包含总体参数的概率
- D、保证总体参数落入置信区间的概率
正确答案:C -
第22题:
对正态总体均值进行区间估计时,其它条件不变,置信水平1-α越小,则置信上限与置信下限的差()
- A、越大
- B、越小
- C、不变
正确答案:B -
第23题:
多选题θ是总体的一个待估参数,θL,θU是其对于给定α的1-α的置信下限与置信上限。则1-α置信区间的含义是( )。A所构造的随机区间[θL,θU]覆盖(盖住)未知参数θ的概率为1-α
B由于这个随机区间随样本观测值的不同而不同,它有时覆盖住了参数θ,有时则没有覆盖参数θ
C用这种方法做区间估计时,不能覆盖参数θ的机率相当小
D如果P(θ<θL)=P(θ>θU)=α/2,则称这种置信区间为等尾置信区间
E正态总体参数的置信区间是等尾置信区间,而比例p的置信区间不是等尾置信区间
正确答案: C,E解析:
C项,用这种方法做区间估计时,100次中大约有100(1-α)个区间能覆盖未知参数,不能说机率是大还是小,需要根据α的具体情况来确定;E项,正态总体参数的置信区间及比例p的置信区间都是等尾置信区间。
