一个三角形三个内角度数的比是6:2:1,这个三角形是()。A.锐角三角形B.钝角三角形C.直角三角形D.等边三角形
题目
一个三角形三个内角度数的比是6:2:1,这个三角形是()。
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等边三角形
相似考题
更多“一个三角形三个内角度数的比是6:2:1,这个三角形是()。”相关问题
-
第1题:
一个三角形三个内角度数的比是2:3:7,这个三角形是一个( )。
A 直角三角形
B 纯角三角形
C 等腰三角形
D 等边三角形
正确答案:B
-
第2题:
三角形一个外角小于与它相邻的内角,这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.属于哪一类不能确定
正确答案:C
-
第3题:
如果三角形的一个外角等于和它相邻的内角的4倍,等于与它不相邻的一个内角的2倍,则此三角形各内角如果三角形的一个外角等于和它相邻的内角的4倍,等于与它不相邻的一个内角的2倍,则此三角形各内角的度数是_____________。
正确答案:
720,720,360 -
第4题:
若a是三角形的一个内角,则必有( )
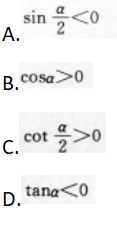 答案:C解析:【考情点拨】本题主要考查的知识点为三角函数值的符号. 【应试指导】
答案:C解析:【考情点拨】本题主要考查的知识点为三角函数值的符号. 【应试指导】

-
第5题:
如果三角形的一个外角小于与它相邻的内角,那么这个三角形一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.任意三角形答案:C解析:三角形的一个外角小于与它相邻的内角,故内角大于相邻外角;根据三角形外角与相邻的内角互补,故内角大于90°,为钝角三角形。 -
第6题:
一个三角形,三个内角的度数都相等,这个三角形一定是()。
- A、任意三角形
- B、等腰三角形
- C、等边三角形
正确答案:C -
第7题:
一个三角形中,三个内角的度数比是3:4:5,这个三角形中,最小的角的度数是()
- A、15°
- B、30°
- C、45°
- D、60°
正确答案:C -
第8题:
一个三角形,三个内角的关系如下:∠1-∠2=10°,∠2-∠3=10°,这个三角形一定是()
- A、锐角三角形
- B、直角三角形
- C、钝角三角形
正确答案:A -
第9题:
如果三角形的一个外角小于与它相邻的内角,那么这个三角形一定是()
- A、锐角三角形
- B、直角三角形
- C、钝角三角形
- D、任意三角形
正确答案:C -
第10题:
单选题在一个三角形里,三个内角度数的比是1:1:2,这个三角形一定是()。A锐角三角形
B直角三角形
C钝角三角形
正确答案: C解析: 暂无解析 -
第11题:
单选题一个三角形中,三个内角的度数比是3:4:5,这个三角形中,最小的角的度数是()A15°
B30°
C45°
D60°
正确答案: D解析: 暂无解析 -
第12题:
单选题一个三角形,三个内角的度数都相等,这个三角形一定是()。A任意三角形
B等腰三角形
C等边三角形
正确答案: A解析: 暂无解析 -
第13题:
一个三角形三个内角度数的比是1:2:3,则这个三角形是( )三角形。
A.等腰
B.钝角
C.锐角
D.直角
正确答案:D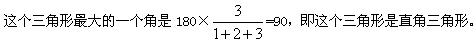
-
第14题:
若三角形三个内角度数的比为2:3:4,则相应的外角比是 .
正确答案:
7:6:5; -
第15题:
由系统误差所产生的天文船位误差三角形,求最概率船位的方法有_________。Ⅰ、在船位误差三角形三个顶角分别作天体方位的平分线Ⅱ、分别对三个天体方位增加2=~4=相同度数Ⅲ、分别对三个高度差增加2'~4'相同高度差Ⅳ、船位误差三角形的三个内角做平分线Ⅴ、作船位误差三角形的三条反中线
A.Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ
B.Ⅰ、Ⅲ、Ⅳ、Ⅴ
C.Ⅱ、Ⅲ、Ⅳ
D.Ⅰ、Ⅲ
正确答案:D
-
第16题:
初中数学《三角形内角和》
一、考题回顾
题目来源:5月18日 上午 吉林省通化市 面试考题
试讲题目
1.题目:三角形内角和
2.内容:
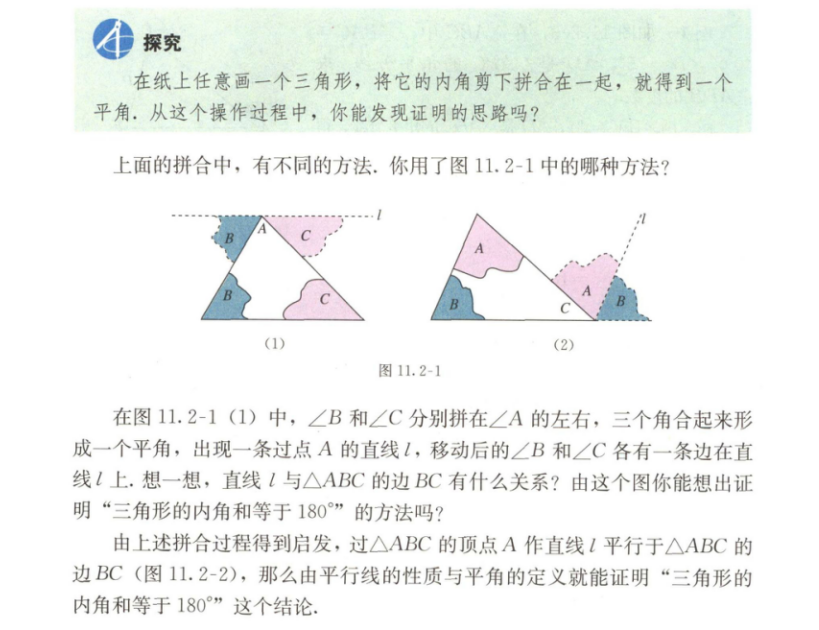
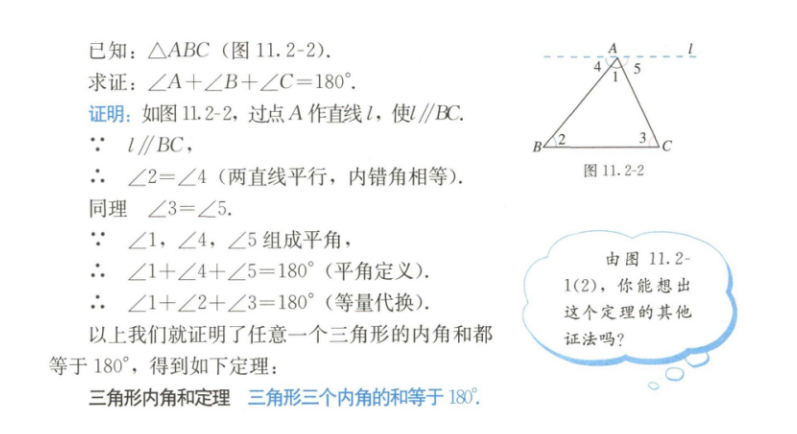
3.基本要求:
(1)能够证明三角形的内角和是180°,并解决相关问题。
(2)试讲十分钟;
(3)要有合适的板书。
答辩题目
1.在验证三角形的内角和的过程中运用了哪些教学方法?
2.本节课的在教材中的地位和作用?答案:解析:二、考题解析
【教学过程】
(一)导入新课
回顾小学阶段学习三角形内角和定理时,利用剪一剪、拼一拼的实验验证方法,通过复习导入引出课题。
(二)新知探索
组织学生进行小组讨论,用拼合的方法探究三角形内角和的证明思路。
引导学生思考将一个三角形的两个角剪下来拼到第三个角的顶点处有哪些方法?发现了哪些问题?四人小组进行探究讨论,再各组派代表在全班进行交流。
在交流的过程中出现了多种拼合方法,教师组织学生集体评价,并及时引导学生展开讨

【答辩题目解析】
1. 在验证三角形的内角和的过程中运用了哪些教学方法?
【参考答案】
在验证三角形的内角和的过程中运用了小组讨论和自主探究的教学方法。组织学生进行小组讨论,用拼合的方法探究三角形内角和的证明思路。引导学生思考将一个三角形的两个角剪下来拼到第三个角的顶点处有哪些方法?发现了哪些问题?四人小组进行探究讨论,再各组派代表在全班进行交流。然后让学生自主探究通利用数学方法证明三角形的内角和定理?通过这样的教学方法,可以充分体现学生的主体性。
2. 本节课的在教材中的地位和作用?
【参考答案】
本节课选自人教版初中数学八年级上册第十一章第二节内容《三角形的内角》第一课时,它是在学生掌握了三角形的特征和分类的基础上教学的。其中三角形内角和的探索和证明过程是本节课的重要教学内容。本节课的内容又是多边形内角和的基础,具有承前启后的作用。 -
第17题:
有一个三角形三个内角观测值之和与180°之差为-2°,此值称为测量误差
正确答案:错误 -
第18题:
甲三角形与乙三角形的底边长的比是2:1,高的比是1:2,那么甲三角形与乙三角形面积的比是()
- A、2:1
- B、1:2
- C、1:1
- D、3:2
正确答案:C -
第19题:
在一个三角形里,三个内角度数的比是1:1:2,这个三角形一定是()。
- A、锐角三角形
- B、直角三角形
- C、钝角三角形
正确答案:B -
第20题:
一个三角形,其中一个角的度数等于另外两个角的度数之和,这个三角形一定是()。
- A、锐角三角形
- B、直角三角形
- C、钝角三角形
正确答案:B -
第21题:
单选题甲三角形与乙三角形的底边长的比是2:1,高的比是1:2,那么甲三角形与乙三角形面积的比是()A2:1
B1:2
C1:1
D3:2
正确答案: C解析: 暂无解析 -
第22题:
单选题一个三角形,三个内角的关系如下:∠1-∠2=10°,∠2-∠3=10°,这个三角形一定是()A锐角三角形
B直角三角形
C钝角三角形
正确答案: C解析: 暂无解析 -
第23题:
单选题如果一个三角形的两个内角度数的和等于第三个内角的度数,那么这个三角形是()。A钝角三角形
B锐角三角形
C直角三角形
D无法判断
正确答案: A解析: 暂无解析 -
第24题:
单选题欲确定一个平面三角形至少需要观测其几个内角()。A一个内角;
B两个内角;
C三个内角。
正确答案: B解析: 暂无解析
