9、（选择题）设X,Y相互独立，且X,Y的分布函数分别为FX（x)，FY（y)，令Z = min（X,Y)，则Z的分布函数FZ （z) = （） a.1-[1- FX （x )] [1-FY （y ) ] b. FX （x ) FY （y ) c. 1- FX （x ) FY （y ) d. [1- FX （x )] [1-FY （y ) ]
题目
9、（选择题）设X,Y相互独立，且X,Y的分布函数分别为FX（x)，FY（y)，令Z = min（X,Y)，则Z的分布函数FZ （z) = （） a.1-[1- FX （x )] [1-FY （y ) ] b. FX （x ) FY （y ) c. 1- FX （x ) FY （y ) d. [1- FX （x )] [1-FY （y ) ]
相似考题
更多“9、（选择题）设X,Y相互独立，且X,Y的分布函数分别为FX（x)，FY（y)，令Z = min（X,Y)，则Z的分布函数FZ （z) = （） a.1-[1- FX （x )] [1-FY （y ) ] b. FX （x ) FY （y ) c. 1- FX （x ) FY （y ) d. [1- FX （x )] [1-FY （y ) ]”相关问题
-
第1题：
下列关于部分函数依赖的叙述中，哪一条是正确的?
A．若X→Y，且存在属性集Z，Z∩Y
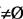，Y→Z，则称Y对X部分函数依赖B．若X→Y，且存在属性集Z，Z∩Y
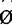，Y→Z，则称Y对X部分函数依赖C．若X→Y，且存在X的真子集X'，X'→Y，则称Y对X部分函数依赖
D．若X→Y，且对于X的任何真子集X'，都有X'→Y\，则称Y对X部分函数依赖
正确答案：C
解析：本题是对函数依赖定义和公理的考查。选项A、B显然是不正确的；按照函数部分依赖的定义选项C(若X→Y，且存在X的真子集X'，X'→Y，则称Y对X部分函数依赖)是正确的。而D(若X→Y，且对于X的任何真子集X'，都有X'≠＞Y，则称Y对X部分函数依赖)是错误的，因为若X→Y，且对于X的任何真子集X'，都有X'≠＞Y，则称Y对X是完全函数依赖。所以本题正确答案为选项C。 -
第2题：
窗体上有名称为Commandl的命令按钮。事件过程及2个雨数过程如下：
Private Sub Commandl_Click()
Dim X As Integer，Y As Integer，z
x=3
Y=5
z=fy(Y)
Print fx(fx(x))，y
End Sub
Function fx(ByVal a As Integer)
a=a+a
fx=a
End Function
Function fy(ByRef a As Integer)
a=a+a
fy=a
End nlnction
运行程序，并单击命令按钮，则窗体上显示的2个值依次是【 】和【 】。
正确答案：1210
12,10 解析：函数fy中的参数a是按地址传递，函数fx中的参数a是按值传递，所以执行z=fy(y)后，y的值为10，z的值为10，x的值为3，而执行fx(fx(x))后，fx(fx(x))的为12。 -
第3题：
下列关于部分函数依赖的叙述中，哪一条是正确的?______。
A．若X→Y，且存在属性集Z，Z∩Y≠Φ，X→Z，则称Y对X部分函数依赖
B．若X→Y，且存在属性集Z，Z∩Y=Φ，X→Z，则称Y对X部分函数依赖
C．若X→Y，且存在X的真子集X'，X'→Y，则称Y对X部分函数依赖
D．若X→Y，且对于X的任何真子集X'，都有X'
Y，则称Y对X部分函数依赖正确答案：C
-
第4题：
设随机变量X,Y相互独立,它们的分布函数为Fx(x),F(y),则Z=min{X,Y}的分布函数为().
答案：C解析：FZ(z)=P(Z≤z)=P(min{X,Y}≤z)=1-P(min{X,Y}>z) =1-P(X>z,Y>z)=1-P(X>z)P(Y>z)
=1-【1-P(X≤z)】【1-P(Y≤z)】=1-【1-FX(z)】【1-FY(z)】，选(C). -
第5题：
设随机变量X的概率密度为fx(x)=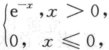
求y=e^x的概率密度FY(y).答案：解析：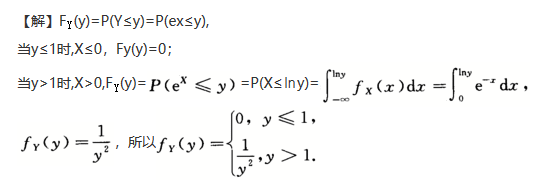
-
第6题：
计算导线全长闭合差的公式是：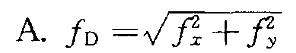
B. K=fd/∑D=1/M
C.fx=ΣΔx- (x终-x始)
D.fy=ΣΔy- (y终-y始)答案：A解析：提示：导线全长闭合差的计算公式。 -
第7题：
力矢F（投影Fx，Fy，Fz）作用点坐标为（x，y，z），则此力对z轴的矩是（）。
- A、yFz—zFy
- B、xFy—yFx
- C、zFx—xFz
- D、zFz
正确答案:B -
第8题：
实腹式轴压杆绕x,y轴的长细比分别为λx、λy，对应的稳定的系数分别为fx、fy，若λx=λy，则（）。
- A、fx>fy
- B、fx=fy
- C、fx<fy
- D、需要根据稳定性分类判别
正确答案:D -
第9题：
单选题设f（x，y，z）＝exyz2，其中z＝z（x，y）是由x＋y＋z＋xyz＝0确定的隐函数，则fx′（0，1，－1）＝（ ）。Ae
B2e
C0
D1
正确答案： B解析：
构造函数F（x，y，z）＝x＋y＋z＋xyz，则有∂z/∂x＝－Fx′/Fz′＝－（1＋yz）/（1＋xy），（∂z/∂x）|（0，1，－1）＝0，又由f（x，y，z）＝exyz2，得fx′＝exyz2＋exy·2z·zx′，
代入（0，1，－1），得fx′（0，1，－1）＝e0×1×（－1）2＋e0×1×2×（－1）×0＝1。 -
第10题：
单选题若函数z＝f（x，y）满足∂2z/∂y2＝2，且f（x，1）＝x＋2，fy′（x，1）＝x＋1，则f（x，y）＝（ ）。Ay2＋（x－1）y＋2
By2＋（x＋1）y＋2
Cy2＋（x－1）y－2
Dy2＋（x＋1）y－2
正确答案： D解析：
因为∂2z/∂y2＝2，等式两边对y积分得，fy′（x，y）＝2y＋φ1（x）。
又fy′（x，1）＝x＋1，则φ1（x）＝x－1。
故fy′（x，y）＝2y＋x－1。两边再对y积分得f（x，y）＝y2＋xy－y＋φ2（x）。
又f（x，1）＝x＋2，故φ2（x）＝2。
故f（x，y）＝y2＋xy－y＋2。 -
第11题：
单选题设f（x，y）与φ（x，y）均为可微函数，且φy′（x，y）≠0。已知（x0，y0）是f（x，y）在约束条件φ（x，y）＝0下的一个极值点，下列选项正确的是（ ）。A若fx′（x0，y0）＝0，则fy′（x0，y0）＝0
B若fx′（x0，y0）＝0，则fy′（x0，y0）≠0
C若fx′（x0，y0）≠0，则fy′（x0，y0）＝0
D若fx′（x0，y0）≠0，则fy′（x0，y0）≠0
正确答案： A解析：
设z＝f（x，y）＝f（x，y（x）），由题意可知∂z/∂x＝fx′＋fy′·（dy/dx）＝0。
又φ（x，y）＝0，则dy/dx＝－φx′/φy′。故fx′－（φx′/φy′）fy′＝0。又φy′≠0，则fx′φy′＝φx′fy′。所以当fx′≠0时fy′≠0。 -
第12题：
填空题设f（x，y，z）＝exyz2，其中z＝z（x，y）是由x＋y＋z＋xyz＝0确定的隐函数，则fx′（0，1，－1）＝____。正确答案： 1解析：
构造函数F（x，y，z）＝x＋y＋z＋xyz，则有∂z/∂x＝－Fx′/Fz′＝－（1＋yz）/（1＋xy），（∂z/∂x）|（0，1，－1）＝0，又由f（x，y，z）＝exyz2 ，得fx′＝exyz2＋exy·2z·zx′，代入（0，1，－1），得fx′（0，1，－1）＝e0×1×（－1）2＋e0×1×2×（－1）×0＝1。 -
第13题：
下列关于部分函数依赖的叙述中，______是正确的。
A．若X→Y，且存在属性集Z，Z∩Y≠Φ，X→Z，则称Y对X的部分函数依赖
B．若X→Y，且存在属性集Z，Z∩y＝Φ，X→Z，则称Y对X的部分函数依赖
C．若X→Y，且存在X的真子集X'，X'→Y，则称Y对X的部分函数依赖
D．若X→Y，且对于X的任何真子集X'，都有X'→Y，则称Y对X的部分函数依赖
正确答案：C
解析：在关系模式RU，F＞中，如果X→Y，且存在X的一个真子集X'，有X'→Y，则称Y对X的依赖为部分函数依赖。这是部分函数依赖的定义。 -
第14题：
下列关于部分函数依赖的叙述中，哪一条是正确的?
A．若X→Y，且存在属性集Z，Z∩Y≠
，Y→Z，则称Y对X部分函数依赖B．若X→Y，且存在属性集Z，Z∩Y=
，Y→Z，则称Y对X部分函数依赖C．若X→Y，且存在X的真子集X'，
，则称Y对X部分函数依赖D．若K→X，且对于X的任何其子集又X'，都有X'→Y，则称Y对X部分函数依赖
正确答案：C
解析：选项A、B显然是不正确的；按照函数部分依赖的定义，选项C(若X→Y，且存在X的真子集X'，X'→Y，别称Y对X部分数依赖)正确的。而D(若X→Y，且对于X的任何真子集X'，都有，则称Y对X部分函数依赖)是错误的，因为若X→Y，且对于X的任何真子集X'，都有X→Y，则称对Y对X是完全函数依赖。 -
第15题：
函数z=f（x，y）处可微分，且fx'（x0，y0）=0，fy'（x0，：y0）=0，则f （x，y）在P0（x0，y0）处有什么极值情况？A.必有极大值
B.必有极小值
C.可能取得极值
D.必无极值答案：C解析：提示：z=f（x，y）在p0（x0，y0）可微，且fx'（x0，y0）=0，fy'（x0，y0）=0，是取得极值的必要条件，因而可能取得极值。 -
第16题：
设随机变量X,Y相互独立,它们的分布函数为Fx(x),FY(y),则Z=max{X,Y)的分布函数为().
答案：B解析：FZ(z)=P(Z≤z)=P(max{X,Y}≤z)=P(X≤z,Y≤z)=P(X≤z)P(Y≤z)-FX(z)FY(z)，选(B). -
第17题：
设随机变量X和Y相互独立,且分布函数为Fx(x)=
,Fy(y)=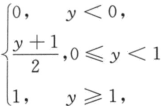
,令U=X+Y,则U的分布函数为_______.答案：解析：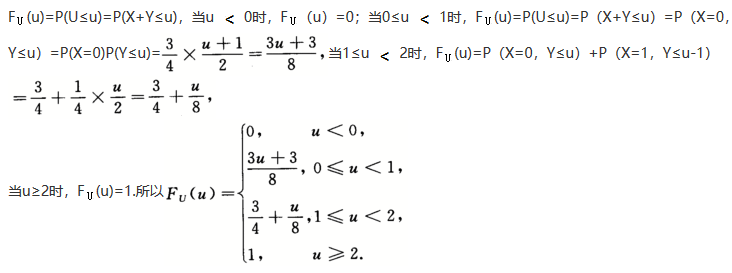
-
第18题：
用卡尺测量尺寸时，被测量Y与输入量X，通过函数关系f来表达的数学模型为（ ）。
A. Y=Z(Xi) B. Y=f(X) C. Y = X D. Y = FX答案：C解析：函数关系式可能非常复杂，以至于不能明确地表示出来。当然，数学模型有时也 可能简单到如用卡尺测量工件的尺寸，工件的尺寸就等于卡尺的示值。 -
第19题：
设随机变量X，Y独立同分布，且X的分布函数为F（x），则Z=max{X，Y}的分布函数为（）
- A、F2（x）
- B、F（x）F（y）
- C、1-[1-F（x）]2
- D、[1-F（x）][1-F（y）]
正确答案:A -
第20题：
设随机变量X的概率密度为fX（x），随机变量Y的概率密度为fY（y），则二维随机变量（X、Y）的联合概率密度为fX（x）fY（y）。
正确答案:错误 -
第21题：
单选题设X，Y是相互独立的随机变量，其分布函数分别为FX（x）、FY（y），则Z＝min（X，Y）的分布函数是（ ）。AFZ（z）＝max[FX（x），FY（y）]
BFZ（z）＝min[FX（x），FY（y）]
CFZ（z）＝1－[1－FX（x）][1＋FY（y）]
DFZ（z）＝FY（y）
正确答案： D解析：
FZ（z）＝P{Z≤z}＝P{min（X，Y）≤z}＝1－P{min（X，Y）＞z}＝1－P{X＞z，Y＞z}＝1－P{X＞z}P{Y＞z}＝1－[1－FX（x）][1－FY（y）]，故应选C。 -
第22题：
问答题设随机变量(X,Y)的概率密度为 求：(1)系数k. (2)边缘概率密度fX(x),fY(y). (3)P{X+Y>1}.正确答案：解析： -
第23题：
单选题实腹式轴压杆绕x,y轴的长细比分别为λx、λy，对应的稳定的系数分别为fx、fy，若λx=λy，则（）。Afx>fy
Bfx=fy
Cfx<fy
D需要根据稳定性分类判别
正确答案： B解析： 暂无解析 -
第24题：
单选题设随机变量（X，Y）服从二维正态分布，且X与Y不相关，fX（x），fY（y）分别表示X，Y的概率密度，则在Y＝y的条件下，X的条件概率密度fX|Y（x|y）为（ ）。AfX（x）
BfY（y）
CfX（x）fY（y）
DfX（x）/fY（y）
正确答案： D解析：
因为（X，Y）服从二维正态分布，且相关系数ρ＝0，故X，Y相互独立，故fX|Y（x|y）＝f（x，y）/fY（y）＝fX（x）fY（y）/fY（y）＝fX（x）。