（2）十进制数转换为R进制数时，整数转换采用“除基取余法”，直到商为零；每次相除所得余数为对应的R进制整数的各位数码。余数从右到左排列，首次取得的余数排在最左边（结果的最高位）。

题目

（2）十进制数转换为R进制数时，整数转换采用“除基取余法”，直到商为零；每次相除所得余数为对应的R进制整数的各位数码。余数从右到左排列，首次取得的余数排在最左边（结果的最高位）。

相似考题

1.十进制整数100转换为二进制数是（ ）。A．1100100B．1101000C．1100010D．1110100

2.十进制的整数化为二进制整数的方法是()。A、乘2取整法B、除2取整法C、乘2取余法D、除2取余法

3.十进制整数转换为二进制数一般采用()A、乘2取余法B、乘2取整法C、乘10取余法D、乘10取整法

4.十进制整数转换成二进制数用()方法。A、除2取余法B、乘2取余法C、除2取整法D、乘2取整法

更多“（2）十进制数转换为R进制数时，整数转换采用“除基取余法”，直到商为零；每次相除所得余数为对应的R进制整数的各位数码。余数从右到左排列，首次取得的余数排在最左边（结果的最高位）。”相关问题

  • 第1题：

    十进制转换为二进制的时候，整数部分和小数部分都要采用除2取余法。()


    参考答案：错误

  • 第2题：

    将十进制数转换成二进制数，整数部分的操作是：十进制数的整数部分除以2取余数，直到商为0，将余数顺序排列。()


    正确答案:错

  • 第3题：

    以下关于二、十和十六进制数之间整数转换正确的是(20)。

    A．十进制数439转换成8421BCD码是0100000111001

    B．十进制数2008转换为二进制无符号数是111011000B

    C．十六进制数0F2H转换成十进制数是232

    D．十进制数122转换成十六进制数是7AH


    正确答案：D
    解析：对于选项A中，十进制数439转换成8421BCD码是010000111001而不是010000011001。对于选项B中，十进制数2008转换为二进制无符号数的运算过程是：2008D=1024+512+256+128+64+16+8=011111011000B，而不是111011000B。对于选项C中，十六进制数0F2H转换成十进制数的运算过程是：0F2H=15×161+2×160=242对于选项D中，先将十进制数122转换成二进制数是01111010，再转换成对应的十六进制数是7AH。所以本试题的正确答案是选项D。

  • 第4题：

    无符号二进制整数01001001转换为十进制数的是

    A．69

    B．71

    C．73

    D．75


    正确答案：C
    解析：1001001B=(1×26+0×25+0×24+1×23+1)D=73D。

  • 第5题：

    阅读以下说明和流程图，回答问题1～2，将解答填入答题纸对应的解答栏内。

    [说明]

    给定一个十进制整数A，将其转换为R进制数的方法是：将A的整数部分逐次除以R，直到商等于0为止，将所得的余数由低位到高位排列在一起，就得到了对应R的进制数。以A=11，R=2为例，11÷2=5…1，5÷2=2…1，2÷2=1…0，1÷2=0…1中各式的余数依次为：1，1，0，1，于是与A对应的二进制数为1011。

    下面的流程图实现了将十进制数2597转换为八进制数的功能，其中：

    (1)循环1执行除法运算并将余数依次记录在数组a中(假定数组长度足够长)，如a[1]， a[2]，……，a[k]；

    (2)循环2则用于将这些余数按逆序输出，即a[k]，a[k-1]，……，a[1]；

    (3)图中i,j分别是循环1和循环2中的循环变量；

    (4)图中q用于记录每次除法所得的商值。

    [流程图]

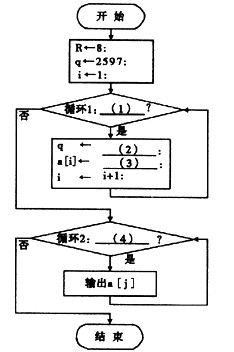
    [问题1]

    将流程图中的(1)～(4)处补充完整，其中(1)～(3)处要求使用C语言格式书写：(1)处为逻辑表达式，(2)、(3)两处为算术表达式；(4)则须按照“循环变量名：循环初值，循环终值，增量”格式描述。

    [问题2]该算法运行的结果(5)。


    正确答案：[问题1](1)q＞0 (2)q/R (3)q%R (4)j:i-11 -1 [问题2](5)5045
    [问题1](1)q＞0 (2)q/R (3)q%R (4)j:i-1,1, -1 [问题2](5)5045 解析：(1)～(3)根据流程图的说明可知：仅当除R所得的商大于零时(即q>0)，循环1会被重复执行；并且循环1的循环体中对q进行一次除法运算，因此商等于q/R，余数a[i]=q％R；
    (4)在开始执行循环2时，i的值是余数的个数加上1,因此，在以j为循环变量逆序输出数组s中有意义的那部分值，应以数组下标i-1为循环初值，以数组下标1为循环终值，以1为增量；
    (5)由于2597÷8=324…5，324÷8=40…4，40÷8= 5…0，5+8=0…5，因此算法运行结果为5045。

  • 第6题：

    对于十进制整数转换为二进制整数，可采用（），将十进制纯小数转换为二进制纯小数时，可采用（）。


    正确答案:除2取余法；乘2取整法

  • 第7题：

    十进制整数100转换为二进制数是（　）

    • A、1100100
    • B、1101000
    • C、1100010
    • D、1110100

    正确答案:A

  • 第8题：

    将十进制整数转化为二进制整数，通常采用（）

    • A、乘2取整法
    • B、加2取整法
    • C、除2取余法
    • D、减2取余法

    正确答案:C

  • 第9题：

    两个数相除，如果商不是整数和有限小数，那么就一定是循环小数；那是因为（）。

    • A、每次除得的余数（不看计数单位），都必须是小于除数的正整数
    • B、小于正整数的个数是有限的
    • C、每次除得的余数（不看计数单位），都必须是小于除数的正整数，而小于正整数的个数是有限的

    正确答案:C

  • 第10题：

    指令“DIVAB”的含义是（）

    • A、A与B进行有符号数相除，商的整数在B中，余数在A中
    • B、A与B进行无符号数相除，商的整数在B中，余数在A中
    • C、A与B进行有符号数相除，商的整数在A中，余数在B中
    • D、A与B进行无符号数相除，商的整数在A中，余数在B中

    正确答案:D

  • 第11题：

    单选题
    十进制整数100转换为二进制数是（　）
    A

    1100100

    B

    1101000

    C

    1100010

    D

    1110100


    正确答案： A
    解析： 二进制整数从右到左的单位是:最右单位是“2的0次幂=1”，次右单位是“2的1次幂=2”，再右单位是“2的2次幂=4”，以此类推。 二进制转化为十进制时，用该单位上的数0或1，与单位相乘，然后相加。
    100(十进制) = 1100100(二进制)

  • 第12题：

    单选题
    将一个十进制正整数转化为二进制数时，采用的方法是（）
    A

    乘2取整法

    B

    除2取余法

    C

    除2取整法

    D

    乘2取余法


    正确答案： D
    解析： 暂无解析

  • 第13题：

    十进制整数转换为二进制数一般采用()。

    A、除2取余法

    B、乘2取整法

    C、乘10取余法

    D、乘10取整法


    参考答案：A

  • 第14题：

    将十进制整数转化为R进制整数的方法是“除基数取余”法。()

    此题为判断题(对，错)。


    参考答案：正确

  • 第15题：

    以下关于二、十、十六进制数之间整数转换正确的是(2)。

    A．十进制数439转换成8421BCD码是0100000011001

    B．十进制数2008转换为二进制无符号数是111011000B

    C．十六进制数0F2H转换成十进制数是232

    D．十进制数122转换成十六进制数是7AH


    正确答案：D
    解析：对于选项A中，十进制数439转换成8421BCD码是010000111001，而不是010000011001。对于选项B中，十进制数2008转换为二进制无符号数的运算过程是：2008D=-1024+512+256+128+64+16+8=011111011000B，而不是111011000B。对于选项C中，十六进制数0F2H转换成十进制数的运算过程是：0F2H=15×161+2×160=242对于选项D中，先将十进制数122转换成二进制数是01111010，再转换成对应的十六进制数是7AH。所以本试题的正确答案是选项D。

  • 第16题：

    二进制正整数11111111转换为十进制数是【 】 。


    正确答案：255
    255 解析：将非十进制数转换成十进制数的方法就是按权展开。111111l1B=1×27+1×26+1×25+1×24+l×23+1×22+1×21+1×20=128+64+32+16+8+4+2+l=255。

  • 第17题：

    数学十进制转换成二进制的方式是用十进制数除2取余而余数自下向上读就是所得的二进制数。


    正确答案:正确

  • 第18题：

    一个R进制数转换为10进制数常用办法是（），一个10进制数转换为R进制数时，整数部分常用方法是（），小数部分常用方法是（）。


    正确答案:基数权重展开法；除R取余法；乘R取整法

  • 第19题：

    将一个十进制正整数转化为二进制数时，采用的方法是（）

    • A、乘2取整法
    • B、除2取余法
    • C、除2取整法
    • D、乘2取余法

    正确答案:B

  • 第20题：

    十进制整数转换为二进制数一般采用（）

    • A、除2取余法
    • B、除2取整法
    • C、除10取余法
    • D、除10取整法

    正确答案:A

  • 第21题：

    将十进制数转换为R进制数时，小数部分采用除R取余法（）


    正确答案:错误

  • 第22题：

    填空题
    一个R进制数转换为10进制数常用办法是（），一个10进制数转换为R进制数时，整数部分常用方法是（），小数部分常用方法是（）。

    正确答案： 基数权重展开法,除R取余法,乘R取整法
    解析： 暂无解析

  • 第23题：

    单选题
    两个数相除，如果商不是整数和有限小数，那么就一定是循环小数；那是因为（）。
    A

    每次除得的余数（不看计数单位），都必须是小于除数的正整数

    B

    小于正整数的个数是有限的

    C

    每次除得的余数（不看计数单位），都必须是小于除数的正整数，而小于正整数的个数是有限的


    正确答案： B
    解析： 暂无解析

  • 第24题：

    判断题
    将十进制数转换为R进制数时，小数部分采用除R取余法（）
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

相关内容