1、消除下列文法G[S]的左递归，获得与其等价的、无左递归的文法G’[S]。 G[S]：S→Qc︱c Q→Rb︱b R→Sa︱a
题目
1、消除下列文法G[S]的左递归，获得与其等价的、无左递归的文法G’[S]。 G[S]：S→Qc︱c Q→Rb︱b R→Sa︱a
相似考题
更多“1、消除下列文法G[S]的左递归，获得与其等价的、无左递归的文法G’[S]。 G[S]：S→Qc︱c Q→Rb︱b R→Sa︱a”相关问题
-
第1题：
文法G[S]:S→AB,B→BB|B不是LR(0)文法。()此题为判断题(对，错)。
正确答案：错误
-
第2题：
考虑下述文法，S为开始符号 G1[S]：S→A A→aAb | ab G2[S] S→AA→aA |a| 下列结论中为真的是(28)。
A．G1是LR(0)文法，G2不是LR(1)文法
B．G2是LR(0)文法，G1不是LR(1)文法
C．G2是LR(1)文法，G1不是LR(1)文法
D．G1和G2都是LR(1)文法
正确答案：A
解析：因为G2存在句子aa，该句子有两棵不同的语法树，所以文法G2是二义性文法。二义性文法不是LR文法，所以B、C、D不正确。选A。 -
第3题：
设有文法G[S]:S→S1|S0|Sa|Sc|a|b|c,下列符号串中()不是该文法的句子。A.ab0
B.a0c01
C.aaa
D.bc10
正确答案：A
-
第4题：
对于以下的文法G[S]，(27)是其句子(从S出发开始推导)。 G(S)：S→M|(S,M) M→P|MP P→a|b|c|…|x|x|z
A．(abc)
B．((a,f))
C．(c,(da))
D．((fac,bb),g)
正确答案：D
解析：对于语言结构的文法表示中的“推导”，就是用产生式的右部替换产生式左部的符号。从文法的开始符号出发，不能推导出(abc)、((a,f))和(c,(da))。对于产生符号串((fac,bb),g)的推导过程如下。
-
第5题：
●试题二
对文法G[S]：S→a|∧|(T)；T→T，S｜S；回答问题1～问题3。
【问题1】
对文法G进行改写，然后对每个非终结符写出不带回溯的递归子程序。
【问题2】
经改写后的文法是否是LL (1) 的?指出它的预测分析表中 (1) ～ (3) 处的内容。
【问题3】
说明输入串(a，a)是否为G的句子。
正确答案：
●试题二［问题1］【答案】改写文法为：(0)S→a；(1)S→∧；(2)S→(T)；(3)T→SN；(4)N→，SN；(5)N→ε非终结符FIRST集FOLLOW集S{a，∧，(}{#，，，}}T{a，∧，c}{}}…N{，，ε}.{}}…对左部为N的产生式可知：FIRST(→，SN)={，}FIRST(→ε)={ε}FOLLOW(N)={}}［问题2］【答案】文法是LL(1)的。(1)→SN；(2)→(T)；(3)→ε［问题3］【答案】输入串(a，a)#是文法的句子。【解析】对于文法S→a｜∧｜(T)T→T,S｜S由于SELECT(N→，SN)∩SELECT(N→ε)={，}∩{}}=，所以文法是LL(1)的。也可由预测分析表中无多重入口判定文法是LL(1)的。(3)对输入串(a，a)#的分析过程为：可见输入串(a，a)#是文法的句子。 -
第6题：
已知文法G［S］：S→A0｜B1，A→S1｜1，B→S0｜0；该文法属于乔姆斯基定义的__（1）__文法，它不能产生串__（2）__。空白（1）处应选择（）
- A、0型
- B、1型
- C、2型
- D、3型
正确答案:D -
第7题：
设有文法G[S]：S→Ap|Bq，A→a|cA，B→b|dB，则FIRST（Ap）为（）
- A、{p，q}
- B、{b，d}
- C、{a，c}
- D、其他
正确答案:C -
第8题：
已知文法G［S］：S→A0｜B1，A→S1｜1，B→S0｜0；该文法属于乔姆斯基定义的__（1）__文法，它不能产生串__（2）__。空白（2）处应选择（）
- A、0011
- B、1010
- C、1001
- D、0101
正确答案:A -
第9题：
设有文法G={{S}，{a}，{S→SaS|ε}，S}，该文法是（）
- A、LL（1）文法
- B、二义性文法
- C、SLR（1）文法
- D、算法优先文法
正确答案:B -
第10题：
问答题设有文法G［W］：W→A0A→A0｜W1｜0，改写文法消除左递归正确答案： 非终结符排序为W，A
则W→A0A→A0｜A01｜0
改写后消除左递归为W→A0A→0A’A’→0A’｜01A’｜ε解析： 暂无解析 -
第11题：
问答题说明下面文法G[S]是二义性文法：S→SaS|SbS|cSd|eS|f正确答案： fafbf是文法G[S]的一个句子，并且有两个不同的最右推导。
（1）S=>SaS=>SaSbS=>SaSbf=>Safbf=>fafbf
（2）S=>SbS=>Sbf=>SaSbf=>Safbf=>fafbf
因此说明此文法有二义性。解析： 暂无解析 -
第12题：
单选题已知文法G［S］：S→A0｜B1，A→S1｜1，B→S0｜0；该文法属于乔姆斯基定义的__（1）__文法，它不能产生串__（2）__。空白（1）处应选择（）A0型
B1型
C2型
D3型
正确答案： A解析： 暂无解析 -
第13题：
设有文法G[S]:S→SAT|T,T→TBR|R,R→PDR|P,P→fSg|e,考察该文法的句型SATBfSgDe,其中哪个是句柄()。ASAT
BB
CfSg
De
正确答案：C
-
第14题：
对文法G[S]：S→a|∧|(T)；T→T，S|S：回答问题1～问题3。
对文法G进行改写，然后对每个非终结符写出不带回溯的递归子程序。
正确答案：改写文法为： (0)S→d (1)S→∧ (2)S→(T) (3)T→SN (4)N→SN (5)N→ε 非终结符 FIRST集 FOLLOW集 S {a∧(} {#}} T {a∧(} {}}… N {ε}． {}}… 对左部为N的产生式可知： FIRST(→SN)；{} FIRST(→ε)：{ε} FOLLOW(N)={}}
改写文法为： (0)S→d (1)S→∧ (2)S→(T) (3)T→SN (4)N→,SN (5)N→ε 非终结符 FIRST集 FOLLOW集 S {a，∧，(} {#,,,}} T {a，∧，(} {}}… N {,,ε}． {}}… 对左部为N的产生式可知： FIRST(→，SN)；{，} FIRST(→ε)：{ε} FOLLOW(N)={}} -
第15题：
已知文法G2=(VT={a，'，'，(,)}，VN={S，L)，S,P)，其中P为 S→(L)|a L→-L，s|s 与G2等价的不含左递归规则的文法是(29)。
A．G21=(VT={a，'，'，(,)}，VN={S，L}，S，P)，其中P为 S→(L)|a L→S，S|S
B．G22=(VT＜a，'，'，(,)}，VN={S，L，L'}，S，P)，其中P为 S→(L)|a L→SL' L'→SL'|ε
C．G23=(VT{a，'，'，(,)}，VN={S，L，L'}，S，P)，其中P为 S→(L)|a L→SL' U→,SL'|ε
D．G24=(VT=(a，'，'，(,)}，VN=＜S，L，L'}，S，P)，其中P为 S→(L)|a L→SL' L→SL'|S
正确答案：C
解析：采用自顶向下的预测分析法首先是等价改写给定的文法，消除文法的左递归和提取产生式的公共左因子。消除直接左递归的方法如下：若A→Aα|β，其中α，β∈(VT∪VN)*，β不以A开始，则关于A的这种形式的产生式可改写成A→βA'A'→αA'|ε一般而言，假设A的产生式为A→Aα1|Aα2|…|Aαn|β1|β2|…|βm其中αI(i=1，2，…，n)不等于ε，βj(j=1，2，…，m)不以A开始，那么上述产生式可改成A→β1A'|β2A'|…|βmA'A'→α1A'|α2A'|…|αnA'|ε消除文法G2中规则的左递归后，其规则变成S→(L)|aL→SL'L'→，SL'|ε -
第16题：
已知文法G2=(VT={a，'，'，(,)}，VN{S,L}，S，P)，其中P为， S→(L)|a L→L，S|S (a，(a，a))是L(G2[S])的句子，这个句子的最左推导是(28)
A．
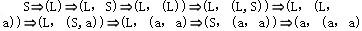
B．
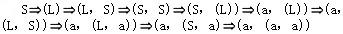
C．
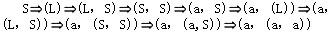
D．
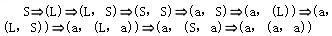正确答案：C
解析：设文法G=(VT，VN，S，P)，A→β∈P，γ，δ∈V*，则称γAδ直接推导出γβδ，表示成：γAδγβδ也称γβδ直接归约到γAδ。对于以上公式，若γ∈VT*，即A是γAδ中最左边的非终结符号，则称以上公式是一个最左推导。若Sa的每一步都是最左推导，则称Sa是一个最左推导，a称为一个左句型。对于以上公式，若δ∈VT*，即A是γAδ中最右边的非终结符号，则称以上公式是一个最右推导。若Sa的每一步都是最右推导，则称Sa是一个最右推导，a称为一个右句型。最右推导也称作规范推导，右句型也称作规范句型。对于句子(a，(a，a))，被选择答案中A是最右推导，C是最左推导，B和D的推导序列中，既有最左推导，又有最右推导。 -
第17题：
● 给定文法G[S]及其非终结符A，FIRST(A)定义为：从A出发能推导出的终结符号的集合（S 是文法的起始符号，为非终结符）。对于文法G[S]：
S→[L] | a
L→L, S| S
其中，G[S]包含的四个终结符号分别为：
a , [ ]
则FIRST(S)的成员包括 （48） 。
（48）
A. a
B. a、[
C. a、[和]
D. a、[、]和，
正确答案：B
-
第18题：
说明下面文法G[S]是二义性文法：S→SaS|SbS|cSd|eS|f
正确答案: fafbf是文法G[S]的一个句子，并且有两个不同的最右推导。
（1）S=>SaS=>SaSbS=>SaSbf=>Safbf=>fafbf
（2）S=>SbS=>Sbf=>SaSbf=>Safbf=>fafbf
因此说明此文法有二义性。 -
第19题：
设有文法G[S]：S→S1|S0|Sa|Sc|a|b|c，下列符号串中不是该文法的句子的是（）
- A、ab0
- B、a0c01
- C、aaa
- D、bc10
正确答案:A -
第20题：
设有文法G［W］：W→A0A→A0｜W1｜0，改写文法消除左递归
正确答案: 非终结符排序为W，A
则W→A0A→A0｜A01｜0
改写后消除左递归为W→A0A→0A’A’→0A’｜01A’｜ε -
第21题：
下列反应中，哪个是表示ΔH=ΔHfA、gB、r（s）的反应？（）
- A、A、g（A、q）+B、r（A、q）=A、gB、r（s）
- B、B、2g（s）+B、r2=2A、gB、r（s）
- C、C、g（s）+1/2B、r2（l）=A、gB、r（s）
- D、D、g（s）+1/2B、r2（S）=A、gB、r（s）
正确答案:C -
第22题：
单选题设有文法G[S]：S→S1|S0|Sa|Sc|a|b|c，下列符号串中不是该文法的句子的是（）Aab0
Ba0c01
Caaa
Dbc10
正确答案： A解析： 暂无解析 -
第23题：
单选题设有文法G[S]：S→Ap|Bq，A→a|cA，B→b|dB，则FIRST（Ap）为（）A{p，q}
B{b，d}
C{a，c}
D其他
正确答案： C解析： 暂无解析 -
第24题：
单选题设有文法G={{S}，{a}，{S→SaS|ε}，S}，该文法是（）ALL（1）文法
B二义性文法
CSLR（1）文法
D算法优先文法
正确答案： D解析： 暂无解析