某次竞赛中，共有20道题，比赛规则为：答对一题得分，答错一题倒扣3分，某同学作答的最后得分为60分，该同学答对15题。 ( )

题目
某次竞赛中，共有20道题，比赛规则为：答对一题得分，答错一题倒扣3分，某同学作答的最后得分为60分，该同学答对15题。 ( )

相似考题

1.光明小学举办数学知识竞赛，一共20题。答对一题得5分，答错一题扣3分，不答得0分。小丽得了79分，她答对几道，答错几道，有几题没答?

2.某次考试，有两种打分方式。一种是答对一题得5分，不答得2分，答错不得分；另一种方法是先给40分，然后答对得3分，不答不得分，答错扣2分。用这两种方式计算，某考生最后都拿到81分。请问这次考试有多少道题?A．17B．18C．20D．21

3.：青风小学3名同学去参加数学竞赛，共10道题，答对一道题得10分，答错一题扣3分。这3名同学都回答了所有的题。小明得87分，小红得了74分，小华得了9分。他们三人一共答对了多少道题？（ ）A．17B．20C．28D．35

4.某次消防知识竞赛，比赛规定，每答对一题得4分，每答错一题倒扣2分，没答的得0分。一共30题中，某消防员只有5题没答，最后他一共得70分。则他一共答对（ ）道题。A．5B．10C．15D．20

更多“某次竞赛中，共有20道题，比赛规则为：答对一题得分，答错一题倒扣3分，某同学作答的最后得分为60分，该同学答对15题。 ( ) ”相关问题

  • 第1题：

    ：10人参加智力竞赛，每人必须回答24个问题。答对一题得5分，答错一题扣3分，结果，（ ）得分最低的为0分，且每个人的得分都不相同。问得分最低的答对几道题，答错几道题?（ ）

    A．816

    B．915

    C．1014

    D．1113


    正确答案：B

     设得分最低的答对2道题，答错Y道题，则 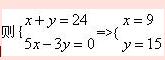，故选B

  • 第2题：

    某次测验有50道判断题，每做对一题得3分，不做或做错一题倒扣1分，某学生共得82分，问答对题数和答错题数相差多少?（　　）A.33　　B.99　　C.17　　D.16


    本题正确答案为D。设做对X道，做错Y道，则可列如下方程：x+y＝50x＝33

    解得3x-y＝82　　　　　　　　y＝17故答对题数与答错题数的差为33-17＝16（题）

     

  • 第3题：

    某次考试，有两种打分方式。一种是答对一题得5分，不答得2分，答错不得分；另一种方法是先给40分，然后答对得3分，不答不得分，答错扣2分。用这两种方式计算，某考生最后都拿到81分。请问，这次考试有多少道题?

    A．17

    B．18

    C．20

    D．21


    正确答案：C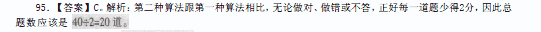

  • 第4题：

    甲、乙解答同一份试卷，共20题，要求每题必做，答对一题得5分，答错一题扣3分，已知甲、乙得分之和为144分，乙答对15题，则甲、乙得分之差是（）。

    A.26
    B.24
    C.60
    D.84

    答案：B
    解析：
    乙得分为15×5－5×3=60分，则甲、乙分数之差为144－60×2=24分，故本题选B。

  • 第5题：

    小王参加电视台的一个智力竞赛节目。节目共有20道快速问答，答对一题得10分，打错或不答均倒扣10分，每人开始有基础分100分。小王最后成绩为220分，问他有几道题没答对？

    A. 5
    B. 6
    C. 3
    D. 4

    答案：D
    解析：
    设答错的题数为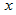道，则答对的题数为20-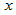。由题意可知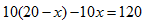，解得。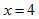

  • 第6题：

    一份中学数学竞赛试卷共15题，答对一题得8分，答错一题或不做答均倒扣4分。有一个参赛学生得分为72，则这个学生答对的题目数是：（　　）

    A. 9
    B. 10
    C. 11
    D. 12

    答案：C
    解析：
    设学生答对x题，则答错或不作答题目数为（15-x）题。答对题目可得的分数为8x分，倒扣分数为4×（15-x）分，根据题意，8x-4×（15-x）=72，求解x=11。故答案为C。

  • 第7题：

    某智力比赛上，对选手得分的要求是，答对一题得5分，答错- -题扣2分，不答的得0分。一共有30道题目，小明最终得了103分，则他答错的题目最多有多少道? ( )


    A.5
    B.6
    C.4
    D.7

    答案：B
    解析：
    设答对x道，答错y道，则有5x-2y=103, x+y≤30,利用代入排除法，从最大的选项开始代入，D选项7,若y=7,则x不为整数，排除: B选项6,若y=6,则x=23, .且23+6- 29满足小于等于30这个条件，因此他最多答错6道题，A. C选项均比B选项更.小，排除，故本题应选B.

  • 第8题：

    有一份选择题试卷共6个小题，其得分标准是：一道小题答对得8分，答错得0分，不答得2分，某位同学得了20分，则他（）

    • A、至多答对一道题
    • B、至少有三个小题没答
    • C、至少答对三个小题
    • D、答错两个小题

    正确答案:D

  • 第9题：

    单选题
    某次测验有50道判断题，每做对一题得3分，不做或做错一题倒扣1分，某学生共得82分，问答对题数和答错题数（包括不做）相差多少？
    A

    33

    B

    39

    C

    17

    D

    16


    正确答案： A
    解析：

  • 第10题：

    单选题
    一份试卷有20道题，答对一题得5分，答错一题扣2分，不答不得分，李玲在这次考试中得了56分，那么她答错了（  ）道题
    A

    2

    B

    3

    C

    5

    D

    6


    正确答案： B
    解析：

  • 第11题：

    某考试卷中有若干选择题，每答对一题加2分，答错或不答一题扣1分，一考生答对的选择题数量是答错或不答的5倍，选择题共得到45分。问试卷中有多少道选择题？（ ）

    A.50

    B.30

    C.25

    D.20


    正确答案：B
    这是一道和差倍比问题。
    （1）设答错的题目数为x，则答对的题目数为5x，有2×5x-x=45，可得x=5，则答对的题目数为5×5=25，题目总数为5+25=30。因此，本题的正确答案为B选项。
    （2）如果答对5题，答错1题，得分应该是9分。现在得了45分，因此试卷中有45/9×（5+1）=30道题目，选B选项。

  • 第12题：

    一份中学数学竞赛试卷共15题，答对一题得8分，答错一题或不做答均倒扣4分。有一个参赛学生得分为72，则这个学生答对的题目数是（ ）。

    A．9

    B．10

    C．11

    D．12


    正确答案：C
    设答对χ道题，则答错或没答的为15-χ，8χ-(15-χ)×4=72，解出χ=11，故选C。

  • 第13题：

    某次考试，有两种打分方式。一种是答对一题得5分，不答得2分，答错不得分：另一种方法是先给40分，然后答对得3分，不答不得分，答错扣2分。用这两种方式计算，某考生最后都拿到81分。请问，这次考试有多少道题？


    正确答案：C
    解析：第二种算法跟第一种算法相比，无论做对、做错或不答，正好每一道题少得2分，因此总题数应该是40+2=20道。

  • 第14题：

    某班参加一次智力竞赛，共a，b，c三题，每题或者得满分或者得0分。其中题a满分20分，题b、题c满分均为25分。竞赛结果：每个学生至少答对了一题，三题全答对的有1人，答对其中两道题的有15人，答对题a的人数与答对题b的人数之和为29，答对题a的人数与答对题c的人数之和为25，答对题b的人数与答对题c的人数之和为20。问这个班的平均成绩是：( )

    A.23分
    B.38分
    C.42分
    D.46分

    答案：C
    解析：
    根据容斥原理.全班人数为17+12+8-15-2x1=20人。这个班的平均成绩为840÷20=42分。

  • 第15题：

    某次竞赛中，共有20道题，比赛规则为：答对一题得5分，答错一题倒扣3分，某同学作答的最后得分为60分，该同学答对15题。(?)


    答案：对
    解析：
    全部答对得分为100，每答错一道题，损失8分，则共答错(100-60)÷8：5题，答对了 15题。

  • 第16题：

    某学院举行“抗战胜利70 周年”知识抢答赛，总共50 道抢答题。比赛规定：答对1 题得3 分，答错1 题扣1 分，不抢答得0 分。王同学在比赛中抢答了25 道题，要使最后得分不少于65 分，则王同学至少要答对（ ）道题。

    A.16
    B.18
    C.23
    D.17

    答案：C
    解析：
    方法一：要求最后得分不少于65 分，假设25 道题都答对，则王同学得25×3=75分，也就是最多失10 分，易知每答错一题实际是减4 分，10÷4 商2，所以最多错2 题，也就是至少答对23 题。故答案为C。

  • 第17题：

    一项考试共有35道试题，答对一题得2分，答错一题扣1分，不答则不得分。一名考生一共得了47分，那么，他最多答对（ ）题。

    A.26
    B.27
    C.29
    D.30

    答案：B
    解析：
    解法一：
    第一步，本题考查不定方程问题，用代入排除法解题。
    第二步，设答对了x道，答错y道，则可知2x－y＝47，存在没答题目的情况，因此x＋y≤35。题干问最多答对题数，则从最大的开始代入。D选项，x＝30，代入2x－y＝47，解得y＝13，此时x＋y超过35，不符；C项x＝29，y＝11，此时x＋y超过35，不符；B项x＝27，y＝7，剩余1道没答，符合题意。
    因此，选择B选项
    解法二：
    第一步，本题考查不定方程问题。
    第二步，设答对了x道，答错y道，则可知2x－y＝47，即y＝2x－47，存在没答题目的情况，因此x＋y≤35。
    第三步，将y＝2x－47代入不等式，得x＋2x－47≤35，即3x≤82，解得x≤27.333，x可取的最大整数值为27，此时y=7，满足题意。
    因此，选择B选项。

  • 第18题：

    有一份选择题试卷共6道小题，其得分标准是：一道小题答对得8分，答错得0分，不答得2分。某位同学得了20分，则他( )。

    • A、至少答对一道小题
    • B、至少有三道小题没答
    • C、至少答对三道小题
    • D、答错两道小题

    正确答案:D

  • 第19题：

    单选题
    某班同学参加智力竞赛，共有CBA，，三题，每题或得0分或得满分。竞赛结果无人得0分，三题全对1人，答对两题15人，答对A题的人数和答对B题的人数之和为25人，答对A题的人数和答对C题的人数之和为29人，答对B题的人数和答对C题的人数之和为20人，那么该班的人数为（）。
    A

    20

    B

    25

    C

    30

    D

    35

    E

    40


    正确答案： E
    解析： 暂无解析

  • 第20题：

    单选题
    一次数学竞赛出10道选择题，评分标准为：基础分10分，答对一题得3分，答错一题扣1分，不答不得分。要保证有4人得分相同，至少要有多少人参加比赛？（　　）
    A

    80

    B

    100

    C

    115

    D

    120


    正确答案： A
    解析：
    一共做10题：最高分40，最低0分；做对9题：最高37分，最低36分；做对8题：最高34分，最低32分；做对7题：最高31分，最低28分；……做对0题：最高10分；最低0分。可知只有39分、38分、35分得不到，故可以得到的分数种类有：41－3＝38种，所以要想4人得分一样，最少的参赛人数是3×38＋1＝115人。

相关内容