在等腰直角三角形ABC中,过直角顶点C在[ACB内部任作一条射线CM,与线段AB交于点M,则AC>AM的概率是_________。
题目
在等腰直角三角形ABC中,过直角顶点C在[ACB内部任作一条射线CM,与线段AB交于点M,则AC>AM的概率是_________。
相似考题
更多“在等腰直角三角形ABC中,过直角顶点C在[ACB内部任作一条射线CM,与线段AB交于点M,则AC>AM的概率是_________。 ”相关问题
-
第1题:
⊿ABC中,∠ABC、∠ACB的平分线相交于点O。
(1)若∠ABC = 40°,∠ACB = 50°,则∠BOC = 。
(2)若∠ABC +∠ACB =116°,则∠BOC = 。
(3)若∠A = 76°,则∠BOC = 。
(4)若∠BOC = 120°,则∠A = 。
(5)你能找出∠A与∠BOC 之间的数量关系吗?
正确答案:
(1)135°;(2)122°;(3)128°;(4)60°;(5)∠BOC = 90°+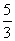 ∠A
∠A
-
第2题:
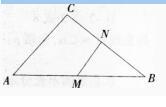
如图,在Rt△ACB中,∠ACB=90o,AC=15,BC=20,M是AB边上的动点(与A,B不重合),N是BC上的动点(与B,C不重合)。
(1)当MN∥AC且BM=12.5时,求线段MN的长。
(2)当MN与AC不平行时,△CMN可能成为直角三角形吗?若可能,请写出线段CN长的取值范围;若不可能,请说明理由。
 答案:解析:
答案:解析:
-
第3题:
在平面直角坐标系中,已知△ABC顶点A(-4,0)和C(4,0),顶点B在椭圆
 答案:解析:
答案:解析:
-
第4题:
在△ABC中,已知AB=5,AC=3,∠A=120°,则BC长为
 答案:A解析:
答案:A解析: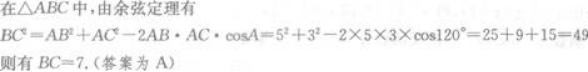
-
第5题:
△ABC中,已知acosA=bcosB,则△ABC是A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰三角形或直角三角形答案:D解析: -
第6题:
如,在直角三角形ABC中,AC=4,BC=3,DE//BC,已知梯形BCDE的面积为3,则DE长为( )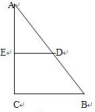
 答案:D解析:
答案:D解析:
-
第7题:
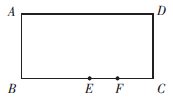
如图所示,在长方形ABC.D中,AD=2AB,E为BC.的中点,F为EC.上任意一点(与E点、C.点不重合),从图形6个点中随机选取3个,能构成直角三角形的概率为:
 A.1/2
A.1/2
B.9/20
C.7/20
D.2/5答案:B解析:从6个点中随机选取3个,总共有

种选法。以A、B两点为准,任选E、F、C、D其中一点均可构成直角三角形。同理,以C、D两点为准,任选E、F、B、A其中一点均可构成直角三角形,总共有
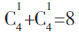
种。同时,因为E为BC中点,且AD=2AB,则△AED也是直角三角形,△AFD不是直角三角形,则所求为(8+1)/20=9。故本题选B。 -
第8题:
在直角三角形ABC中,点D是斜边AB的中点,点P为线段CD的中点,则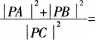 ( )。A、2
( )。A、2
B、4
C、5
D、10答案:D解析:本题主要考查两点问的距离公式,以及坐标法这一重要的解题方法和数形结合的数学思
-
第9题:
如图,Rt△ABC中,AB=6,BC=4,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为__________。
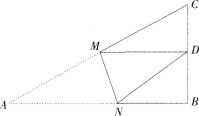 答案:解析:
答案:解析:
-
第10题:
已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1和S2,则S1+S2的值等于4π。
正确答案:错误 -
第11题:
等腰三角形法是逐次将仪器安置在B、C、D三点上观测,要求∠ABC=∠CDE,线段BD=CD。最后,测定出的D正即为直线AB的延长线,唯一不同点是等腰三角形法中照准部旋转的()900的直角。
- A、是
- B、就是
- C、不是
- D、仍是
正确答案:C -
第12题:
单选题在△ABC中,若2cosBsinA=sinC,则△ABC的形状一定是()。A等腰直角三角形
B直角三角形
C等腰三角形
D等边三角形
正确答案: B解析: 暂无解析 -
第13题:
如图.△ABC是一个等腰直角三角形,它与一个正方形叠放在一起,已知AE=EF=FB,⊿EFD的面积是4 cm2,则⊿ABC的面积是________cm2。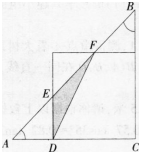 答案:解析:
答案:解析:
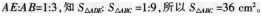
-
第14题:
F1,F2分别为双曲线x2/a2-y2/b2=1(a>0,b>o)的左右焦点,离心率为e,过F1的直线与双曲线左支相交于A,B两点,若△F2AB是点A为直角顶点的等腰直角三角形,则e2=________答案:解析:
-
第15题:
在等腰直角三角形ABC中,过直角顶点C在∠ACB内部任作一条射线CM,与线段AB交于点M,则AC>AM的概率是______。答案:解析:
-
第16题:
在△ABC中,若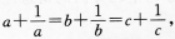 则△ABC必是( )A.直角三角形
则△ABC必是( )A.直角三角形
B.等腰三角形
C.等边三角形
D.钝角三角形答案:C解析:【考情点拨】本题主要考查的知识点为等式的变换. 【应试指导】
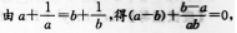
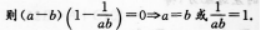
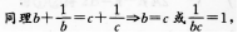
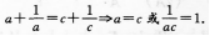
∴a=b=C. -
第17题:
在 ABC中,∠ABC=600,AB=4,BC=6,则AC=()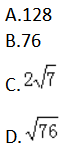 答案:C解析:
答案:C解析: -
第18题:
从正五边形5个顶点中任取4个顶点,构成等腰梯形的概率为: 答案:D解析:如图所示,任取4个顶点相当于任意排除1个顶点,连成四边形。
答案:D解析:如图所示,任取4个顶点相当于任意排除1个顶点,连成四边形。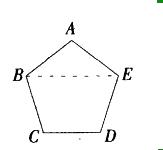

-
第19题:
如图1,在△ABC中,BC = 8 cm,AB的垂直平分线交AB于点D, 交边AC于点E,△BCE的周长等于18 cm,则AC的长等于( ) A、6cm
A、6cm
B、8cm
C、10cm
D、12cm答案:C解析: -
第20题:
如图4,在等腰直角△ABC中,∠B=90o,将△ABC绕顶点A逆时针旋转60o后得到△ADE,则∠BAE=__________度。 答案:解析:105
答案:解析:105 -
第21题:
分别用分析法,综合法证明如下命题。
命题:如图:三角形ABC的角B和角C的角平分线相交于点0,过点O作平行于底边BC的直线,交AB边于点D,交AC边于点E,则DE=BD+EC。
 答案:解析:证明:(1)分析法证明:要证DE=BD+EC.
答案:解析:证明:(1)分析法证明:要证DE=BD+EC.
需证OD=BD,OE=CE,
需证∠DBO=∠DOB,∠ECO=∠EOC,
显然由已知OB为∠DBC的平分线,OC为∠ECB的平分线,且DE∥BC,所以∠DBO=∠DOB,∠ECO=∠EOC,所以命题成立。
(2)综合法证明:
∵OB为∠DBC的平分线,OC为1ECB的平分线,且DE∥BC,
∴∠DBO=∠OBC=∠DOB,∠EC0=∠BC0=∠EOC,
∴BD=OD.EC=OE。
又∵DE=OD+DE
∴DE=BD+EC。 -
第22题:
在△ABC中,若2cosBsinA=sinC,则△ABC的形状一定是()。
- A、等腰直角三角形
- B、直角三角形
- C、等腰三角形
- D、等边三角形
正确答案:C -
第23题:
不等腰直角三角形中对着直角的边叫做()。
正确答案:弦 -
第24题:
判断题已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1和S2,则S1+S2的值等于4π。A对
B错
正确答案: 对解析: 暂无解析
