已知z=2x-y,式中x,y满足则z最大值为__________。
题目
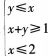
则z最大值为__________。
相似考题
更多“已知z=2x-y,式中x,y满足 ”相关问题
-
第1题:
已知(X,Y)服从均匀分布,联合概率密度函数为

设Z=max{X,Y}求Z的概率密度函数fz(z)
答案:X与Y都服从(0, 1)上的均匀分布,则fx与fy在(0, 1)上恒等于1。
Z = z <==> {X = z && Y <= z} + {Y = z && X < z}
因此,fz(z)dz = fx(z)dz * Integrate[fy(z)dy, (0, z)] + fy(z)dz * Integrate[fx(z)dx, (0, z)]
fz(z)dz = zdz + zdz = 2zdz
故fz(z) = 2z,z属于(0, 1). -
第2题:
以下变量x、y、z均为double类型且已正确赋值,不能正确表示数学式x/y×z的C语言表达式是 ( )
A.x/y * z)
B.x * (1/(y * z))
C.x/y * 1/z)
D.x/y/z
正确答案:A
-
第3题:
设X与Y为相互独立的随机变量,且Var(X)=4,Var(Y)=9,则随机变量Z=2X-Y的标准差为( )。
A.1
B.
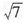
C.
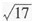
D.5
正确答案:D
解析:因为Var(Z)=Var(2X-Y)=4Var(X)+Var(Y)=4+4+9=25,所以随机变量Z=2X-Y的标准差为:σ(Z)=Var(Z)=5。 -
第4题:
设 X、Y相互独立,X~N(4,1),Y~N(1,4),Z=2X-Y,则A.0
B.8
C. 15
D. 16答案:B解析:提示:由方差性质D(Z) =D(2X)+D(Y) = 4D(X)+D(Y) = 4x1 + 4。 -
第5题:
X、Y、Z 3种金属,已知x可以从Y的盐溶液中置换出Y,X和Z作原电池电极时Z为正极,Y离子的氧化性强于Z离子,则这三种金属的活动性由强到弱的顺序是( )A.X>Y>Z
B.X>Z>Y
C.Z>X>Y
D.Z>Y>X答案:B解析:(1)根据“X可以从Y的盐溶液中置换出Y”,可知金属活动性是X>Y. (2)根据“X和Z作原电池电极时,Z为正极”和活泼金属作负极的判断依据,可知金属活动性是X>Z.
(3)“Y离子的氧化性强于Z离子.”根据金属活动性越强,其阳离子的氧化性越弱;金属活动性越弱,其阳离子的氧化性越强,可知金属活动性是Z>Y.
综上分析可得:X>Z>Y. -
第6题:
已知曲面方程为x-yZ+z2-2x+8y+6z=10,则过点(5,-2.1)的切平面方程为( )。A、2x+3y+2z=0
B、2x+y+2z=lO
C、x-2y+6z=15
D、x-2y+6z=0答案:B解析: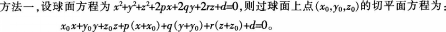
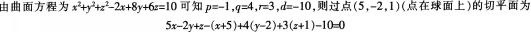

-
第7题:
已知Z=x-y,x和y的中误差分别为mx=±4,my=±3,则Z的中误差为()
- A、±5
- B、±1
- C、±2.64
- D、±4
正确答案:A -
第8题:
设有关系模式R(U,F),其中U={X,Y,Z},F={X→Z,Y→X },则该模式最高满足()
正确答案:2NF -
第9题:
过Z轴和点(1,2,-l)的平面方程是()。
- A、X+2y-z-6=0
- B、2x-Y=0
- C、Y+2z=0
- D、x+z=0
正确答案:B -
第10题:
单选题设X、Y相互独立,X~N(4,1),Y~N(1,4),Z=2X-Y,则D(Z)=()A0
B8
C15
D16
正确答案: C解析: 暂无解析 -
第11题:
单选题设z=φ(x2-y2),其中φ有连续导数,则函数z满足( )。Ax∂z/∂x+y∂z/∂y=0
Bx∂z/∂x-y∂z/∂y=0
Cy∂z/∂x+x∂z/∂y=0
Dy∂z/∂x-x∂z/∂y=0
正确答案: D解析:
令u=x2-y2,则z=φ(u),∂z/∂x=φ′(u)·2x=2xφ′(u),∂z/∂y=-2yφ′(u),故y∂z/∂x+x∂z/∂y=0。 -
第12题:
填空题已知随机变量X~N(-1,1),Y~N(3,1),且X、Y相互独立,Z=X-2Y,则Z~____。正确答案: N(-7,5)解析:
因为X,Y相互独立且服从正态分布,则它们的线性组合也服从正态分布,又E(Z)=E(X)-2E(Y)=-1-2×3=-7,D(Z)=D(X)+4D(Y)=1+4=5,故Z~N(-7,5)。 -
第13题:
已知x,z为带符号纯整数,y为带符号纯小数,而且[X]原=[Y]补=[Z]移=11111101,求出x、y、z的十进制真值:X=(98),Y=(99),Z=(100)。
A.-127
B.125
C.-125
D.1
正确答案:C
-
第14题:
若x,y,z均被定义为整数,则下列表达式能正确表达代数式1/(x*y*z)的是()。
A.1/x*y*z
B.1.0/(x*y*z)
C.1/(x*y*z)
D.1/x/y/(float)z
正确答案:B
-
第15题:
过z轴和点M(1,2,-1)的平面方程是:A. x+2y-z-6=0
B. 2x-y=0
C. y+2z=0
D. x+z=0答案:B解析:

-
第16题:
设 X、Y相互独立,X~N(4,1),Y~N(1,4),Z=2X-Y,则
A.0 B.8 C. 15 D. 16答案:B解析:提示:由方差性质D(Z) =D(2X)+D(Y) = 4D(X)+D(Y) = 4x1 + 4。 -
第17题:
已知∣2x-a∣≤1,∣2x-y∣≤1,则∣y-a∣的最大值为A.1
B.2
C.3
D.4
E.5答案:B解析:由三角不等式∣y-a∣=∣(2x-a)-(2x-y)∣≤∣2x-a∣+∣2x-y∣≤1+1+2 -
第18题:
已知g=lambda x,y=3,z=5:x+y+z,那么表达式g(2)的值为()。
正确答案:10 -
第19题:
设x=-0.01011,y=0.01011,用变形补码计算2x-y。
正确答案: [X]补=11.10101,[Y]补=00.01011
[2X]补=11.01010,[-Y]补=11.10101
[2X]补+[-Y]补=10.11111
结果的双符号位不同,故运算结果溢出.。 -
第20题:
已知intx=10,y=20,z=30;以下语句,if(x>y)z=x;x=y;y=z;执行后x,y,z的值是()
- A、x=10,y=20,z=30
- B、x=20,y=30,z=30
- C、x=20,y=30,z=10
- D、x=20,y=30,z=20
正确答案:B -
第21题:
单选题由x2-xy+y2=C确定的隐函数满足的微分方程是( )。A(x-2y)y′=2x-y
B(x-2y)y′=2x
Cxy′=2x-y
D-2yy′=2x-y
正确答案: C解析:
由x2-xy+y2=C,两边对x求导得2x-y-xy′+2yy′=0,整理得(x-2y)y′=2x-y。 -
第22题:
问答题设x=-0.01011,y=0.01011,用变形补码计算2x-y。正确答案: [X]补=11.10101,[Y]补=00.01011
[2X]补=11.01010,[-Y]补=11.10101
[2X]补+[-Y]补=10.11111
结果的双符号位不同,故运算结果溢出.。解析: 暂无解析 -
第23题:
问答题若函数f(x,y,z)恒满足关系式f(tx,ty,tz)=tkf(x,y,z)就称为k次齐次函数,验证k次齐次函数满足关系式(其中f存在一阶连续偏导数)x∂f/∂x+y∂f/∂y+z∂f/∂z=kf(x,y,z)。正确答案:
为简化计算,可令u=tx,v=ty,w=tz,则f(u,v,w)=tkf(x,y,z),两边对t求导,得x∂f/∂u+y∂f/∂v+z∂f/∂w=ktk-1f(x,y,z),则上式对一切实数t都成立。令t=1,得x∂f/∂x+y∂f/∂y+z∂f/∂z=kf(x,y,z)。解析: 暂无解析
