一名射击运动员连续射靶8次，命中的环数如下：8、9、10、9、8、7、10、8，这名运动员射击环数的众数和中位数分别是（　　）．A.3与8 B.8与8．5 C.8．5与9 D.8与9

题目
一名射击运动员连续射靶8次，命中的环数如下：8、9、10、9、8、7、10、8，这名运动员射击环数的众数和中位数分别是（　　）．

A.3与8
B.8与8．5
C.8．5与9
D.8与9
相似考题

1.一个射击队要从两名运动员中选拔一名参加比赛。在选拔赛上两人各打了10发子弹，成绩如下 : 甲：9.5 10 9.3 9.5 9.6 9.5 9.4 9.5 9.2 9.5乙：10 9 10 8.3 9.8 9.5 10 9.8 8.7 9.9（1）甲、乙成绩的平均数、众数分别是多少？（2）你认为谁去参加比赛更合适？为什么？

2.某运动员射击l0次，成绩（单位：环）如下8 10 9 9 10 8 9 9 8 7则该运动员的平均成绩是___________环．

3.某项射击资格赛后的统计表明，某国四名运动员中，三名运动员的平均环数 加上另一运动员的环数，计算后得到的环数分别为：92、114、138、160，则此 国四名运动员资格赛的平均环数是（ ）。A. 63 B. 126 C. 168 D. 252

4.：某项射击资格赛后的统计表明，某国四名运动员中，三名运动员的平均环数加上另一运动员的环数，计算后得到的环数分别为：92、114、138、160，则此国四名运动员资格赛的平均环数是（ ）环。A．63B．126C．168D．252

更多“一名射击运动员连续射靶8次，命中的环数如下：8、9、10、9、8、7、10、8，这名运动员射击环数的众数和中位数分别是（　　）． ”相关问题

  • 第1题：

    一个射击运动员的准确率是80%，那么他连续射击5 次，有4 次命中的概率是（ ）

    A B C D


    正确答案：A

  • 第2题：

    某个学生参加军训，进行打靶训练，必须射击10次，他第6、第7、第8、第9次射击中，分别得了9．0环、8．4环、8．1环、9．3环，他的前9次所得的平均环数高于前5次设计的平均环数。如果他要使10次的平均环数超过8．8环，那么他在第1O次射击至少要得多少环（每次射击所得环数都精确到O．1环）?（ ）

    A：9．9

    B．9．8

    C．9．7

    D．9．6


    正确答案：A
    由于第6，7，8，9次射击的成绩的和为9．0+8．4+8．1+9．3=34．8，其平均值为34．8÷4=8．7，又因为他的前9次所得的平均环数高于前5次射击的平均环数，所以前5次的平均成绩小于8．7环，这样他的前5次的总成绩最多可得8．7×5—0．1=43．4。设第10次射击中了x环，则x>8．8×10—(34．8+43．4)，x>9．8，故选A。

  • 第3题：

    某射击运动员每次射击命中10环的概率是80%，5次射击有4次命中10环的概率是

    A.80%

    B.63.22%

    C.40.96%

    D.32.81%


    正确答案：C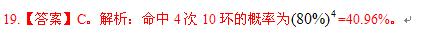

  • 第4题：

    某射击运动员每次射击命中10环的概率是80%,5次射击有4次命中10环的概率是:

    A.80% B.63,22%

    C.40.96% D32.81%


    正确答案：C
    19．C【解析】命中4次10环的概率为(80%)4=40.96%.

  • 第5题：

    射击用的靶子是由若干个同心圆组成，最中心的圆代表10环，而10环外圈的一个圆环代表9环。在随机射击时，若要使得击中10环和9环的概率相同，那么10环外圈半径与9环外圈半径的比值为 () 。


    答案：D
    解析：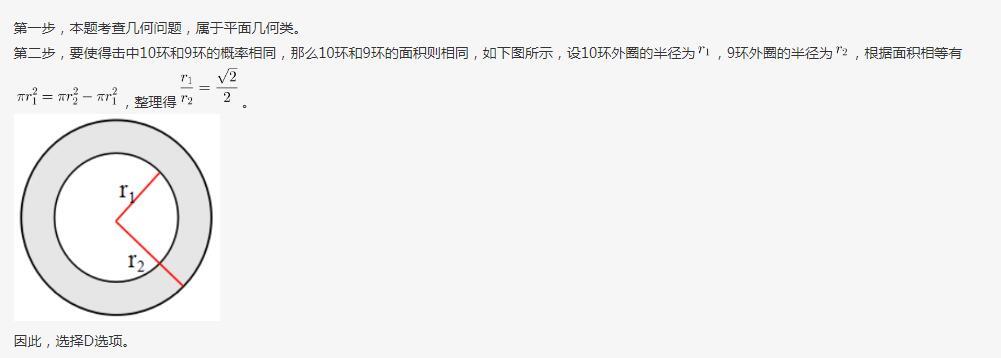

  • 第6题：

    小王打靶共用了10发子弹，全部命中，都在10环、8环和5环上，总成绩为75环，则命中10环的子弹数是（ ）

    A．1发
    B．2发
    C．3发
    D．4发

    答案：B
    解析：
    设他命中10环、8环、5环分别为X、Y、Z发，列式可得：x+y+z=10 10x+8y+5z=75，由于10X尾数必为0，要想得到75，5Z尾数必为5，即Z为奇数。8Y尾数必为0，Y必须能被5整除，Y=5时，符合题意；Y≥10时，结果最小也要大于80，不符合题意。因此，将Y=5代入方程组，解得x=2,z=3。B项当选。

  • 第7题：

    一个射手连续射靶22次，其中3次射中10环，7次射中9环，9次射中8环，3次射中7环．则射中环数的中位数和众数分别为（）

    • A、8，9
    • B、8，8
    • C、8.5，8
    • D、8.5，9

    正确答案:B

  • 第8题：

    有一组数值：9、6、10、8、12、11、8、8、9，其中位数是（）、众数是（）。


    正确答案:9；8

  • 第9题：

    一名射击运动员连续射靶8次，命中的环数如下：8、9、10、9、8、7、10、8，这名运动员射击环数的众数和中位数分别是（）。

    • A、3与8
    • B、8与8.5
    • C、8.5与9
    • D、8与9

    正确答案:B

  • 第10题：

    单选题
    一个射手连续射靶22次，其中3次射中10环，7次射中9环，9次射中8环，3次射中7环．则射中环数的中位数和众数分别为（）
    A

    8，9

    B

    8，8

    C

    8.5，8

    D

    8.5，9


    正确答案： A
    解析： 暂无解析

  • 第11题：

    单选题
    射箭运动员进行训练，10支箭共打了93环，且每支箭的环数都不低8环。问命中10环的箭数最多能比命中9环的多几支？（）
    A

    2

    B

    3

    C

    4

    D

    5


    正确答案： C
    解析： 解析1：由题可知，”每支箭的环数都不低于8环”，所以环数只能取8、9、10环。假设10支箭都打了8环，则最低要打80环，而实际打的93环则是由于有9环和10环的贡献。与80环相比，每一个9环相当于多1环，每一个10环相当于多2环，所以设10环的有a支，9环的b支，则得到方程2a+b=93-80。这时，利用代入法，从”最多”的选项开始代入，a-b=5，解得a=6，b=1，即10环的是6支，9环是1支，8环是3支，可以成立。故正确答案为D。
    解析2：从另一个极端出发，如果每支箭的环数都打中10环，应该是100环，而实际为93环，少了7环。现在要求中10环的箭数”最多”能比命中9环的多几支，即要求10环尽量多，同时9环尽量少。所以少的7环尽可能由8环的箭产生，但是由于每支8环只能差2的整数倍，所以最多差6环，还需要有一支9环的。所以10环6支，9环1支，8环3支可以让差距最大。故正确答案为D。速解如果列方程，属于不定方程，未知数的个数多于方程个数，需要靠代入法解决。而题目真正的考点在于”最多”这个词的理解，即10环尽量多，9环尽量少，在这个前提下分析题目，才能得到最简的方式。

  • 第12题：

    填空题
    有一组数值：9、6、10、8、12、11、8、8、9，其中位数是（）、众数是（）。

    正确答案： 9,8
    解析： 暂无解析

  • 第13题：

    某个学生参加军训，进行打靶训练，必须射击10次，他第6、第7、第8、第9次射击中，分别得了9．O环、8．4环、8．1环、9．3环，他的前9次射击所得的平均环数高于前5次射击的平均环数。如果他要使10次射击的平均环数超过8．8环，那么他在第10次射击至少要得多少环（每次射击所得环数都精确到0．1环）?（ ）

    A．9．9

    B．9．8

    C．9．7

    D．9．6


    正确答案：A
    由于第6，7，8，9次射击的成绩的和为9.0+8.4+8.1+9.3=34.8，其平均值为34.8/4=8.7，又因为他的前9次所得的平均环数高于前5次射击的平均环数，所以前5次的平均成绩小于8.7环。所以前5次成绩最多可得8.7*5-0.1=43.4(环)。设第10次射击中了x环，则 x>88-78.2, x>9.8,所以第10次射击至少得9.9环。故选A。

  • 第14题：

    一组数据6、8、7、8、10、9的中位数和众数分别是

    A．7和8

    B．8和7

    C．8和8

    D．8和9


    正确答案：C

  • 第15题：

    小明每次射击命中10环的概率是50%，5次射击都没有命中10环的概率是（ ）。

    A．3.125%

    B．5%

    C．40%

    D．50%


    正确答案：A

  • 第16题：

    甲、乙两名射击运动员参加某次运动会射击比赛，各进行了10次射击，成绩如下表(单位：环)：

    (1)求甲运动员10次射击的环数的中位数；
    (2)请你用一个统计量评价这两名运动员的成绩哪一个更好.


    答案：
    解析：
    解：(1)将甲运动员的射击环数按从小到大的顺序排列：7.2、7.5、7.8、8.4、8.7、9.9、

    (2)甲运动员的射击环数平均数为：

    乙运动员的射击环数平均数为：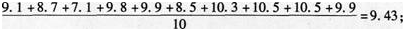

    因为甲平<乙平，所以乙运动员的成绩更好-点.

  • 第17题：

    射箭运动员进行训练，10支箭共打了 93环，且每支箭的环数都不低于8环。问命中10环的箭数最多能比命中9环的多几支？（）

    A.2支
    B.3支
    C.4支
    D.5支

    答案：D
    解析：
    假设命中10环箭数为x,命中9环箭数为y,则有10x+9y +8(10-x-y)=93即80+2x—y=93，2x—y=13，经试代人可求出x、y。

  • 第18题：

    战士甲进行射击训练，已知甲每次射击击中10环、9环、8环或8环以下的概率分别为0.2，0.3，0.5。现甲独立射击了2次，则甲至少有1次射中10环的概率是（ ）。

    A.0.24
    B.0.36
    C.0.2
    D.0.32

    答案：B
    解析：
    一次射击中甲没射中10环的概率是0.8。则甲独立射击了2次，至少有1次射中10环的概率P=1-0.8×0.8=0.36。

  • 第19题：

    MSC、AUC、VLR、EIR的正确子系统数是多少？（）

    • A、8、6、7、9
    • B、6、8、9、7
    • C、8、10、7、9
    • D、6、10、9、7

    正确答案:C

  • 第20题：

    某同学参加射击训练，共射击了六发子弹，击中的环数分别为3，4，5，7，7，10．则下列说法错误的是（）

    • A、其平均数为6
    • B、其众数为7
    • C、其中位数为7
    • D、其中位数为6

    正确答案:C

  • 第21题：

    射箭运动员进行训练，10支箭共打了93环，且每支箭的环数都不低8环。问命中10环的箭数最多能比命中9环的多几支？（）

    • A、2
    • B、3
    • C、4
    • D、5

    正确答案:D

  • 第22题：

    单选题
    射箭运动员进行训练，10支箭共打了93环，且每支箭的环数都不低于8环。问命中10环的箭数最多能比命中9环的多几支（）
    A

    2

    B

    3

    C

    4

    D

    5


    正确答案： A
    解析： 每支箭的环数都不低于8环，意味着环数只能是8、9、10。设射中8、9、10环分别有x、y、z支箭，显然都是非负整数。有x+y+z=10……（1），8x+9y+10z=93……（2）。为使10环的尽可能多，9环的尽可能少，显然8环的也要尽可能多。我们消去9环的y，得到z-x=3，即10环比8环多3支，10环最多只能是6支，这时8环3支，9环1支，相差是5支，而这已经是选项中最多的一项，因此选D。

  • 第23题：

    单选题
    一名射击运动员连续射靶8次，命中的环数如下：8、9、10、9、8、7、10、8，这名运动员射击环数的众数和中位数分别是（）。
    A

    3与8

    B

    8与8.5

    C

    8.5与9

    D

    8与9


    正确答案： C
    解析： 众数是指在一个数列中，出现频率最多的一个数；中位数是指对一组数进行排序（从大到小或从小到大）后，正中间的一个数（数字个数为奇数）或者中间两个数的平均数（数字个数为偶数）。从题中观察可得8出现了3次，出现次数最多，对该组数字进行排序（从小到大）为：7、8、8、8、9、9、10、10，中间两个数是8和9，所以其中位数是（8+9）÷2，即8.5，答案为B。

  • 第24题：

    单选题
    某射击运动员每次射击命中10环的概率是80%，5次射击有4次命中10环的概率是（    ）。
    A

    80%

    B

    63.22%

    C

    40.96%

    D

    32.81%


    正确答案： C
    解析：

相关内容