已知函数y=4/(x-3)，当3＜x≤4，y的最大值为4，y的最小值为-4。()

题目
已知函数y=4/(x-3)，当3＜x≤4，y的最大值为4，y的最小值为-4。()

相似考题

1.若有如下程序： SET TALK OFF INPUT TO X FOR i=1 TO 3 INPUT TO Y IF Y＞X X=Y ENDIF ENDFOR ?X RETURN 本程序的功能是( )。A．求3个数中的最大值B．求4个数中的最大值C．求3个数中的最小值D．求4个数中的最小值

2.已知函数 y=x²-4x+3。（1）画出函数的图象；（2）观察图象，当x取哪些值时，函数值为0？

3.执行以下语句的结果为______。 int x=3,y;int*px=&x;y=*px++;A．x=3,y=4B．x=3,y=3C．x=4,y=4D．x=3,y不知

4.填空：（1）已知函数 y=2（x+1）²+1，当x＜____时，y随x的增大而减小，当x＞ _____时，y随x的增大而增大，当x=______时，y最_____；（2）已知函数 y=-2x²+x-4，当x＜_____时，y随x的增大而增大，当x＞_____时，y随x的增大而减小，当x=______时，y最_____；（3）二次函数 y=ax²+bx+c，a ＞0 ,当x＜_____时，y随x的增大而减小，当x＞_____时，y随x的增大而增大，当x=______时，y最_____；（4 )二次函数 y=ax²+bx+c，a ＜0 ,当x＜_____时，y随x的增大而增大，当x＞_____时，y随x的增大而减小，当x=______时，y最_____。

参考答案和解析
答案：错
解析：
更多“已知函数y=4/(x-3)，当3＜x≤4，y的最大值为4，y的最小值为-4。()”相关问题

  • 第1题：

    已知y与4x－1成正比例，且当x=3时，y=6，写出y与x的函数关系式 ____。


    正确答案：
    －2   

  • 第2题：

    曲线y=x4-3在点(1，-2)处的切线方程为（）

    A.2x-y-6=0
    B.4x-y-6=0
    C.4x-y-2=0
    D.2x-y-4=0

    答案：B
    解析：
    【考情点拨】本题考查了曲线上一点处的切线方程的知识点．

  • 第3题：

    一个竞争性企业只使用一种生产要素z来生产产品y。当0≤z≤4时，企业的生产函数为y=x1.5；当x>4时，企业的生产函数为y= 4+x。如果产品y的价格为每单位1美元，生产要素z的价格为每单位3美元，为使厂商的利润最大化，z的最优投入量为( )。

    A.16/9
    B.4
    C.O
    D.4/3

    答案：B
    解析：

  • 第4题：

    过点A(1,-1)，B(-1,1)且圆心在直线x+y-2=0上的圆的方程是（ ）。

    A.(x-3)2+(y+1)2=4
    B.(x+3)2+(y-1)2=4
    C.(x-1)2+(y-1)2=4
    D.(x+1)2+(y+1)2=4

    答案：C
    解析：

  • 第5题：

    当∣x∣≤4时,函数y=∣x-1∣+∣x-2∣+∣x-3∣的最大值与最小值之差是

    A.4
    B.6
    C.16
    D.20
    E.14

    答案：C
    解析：

  • 第6题：

    已知点的运动方程为x=2t,y=t2-t则其轨迹方程为：

    A. y=t2-t
    B.x=2t
    C. x2-4x-4y=0
    D. x2+2x+4y=0

    答案：C
    解析：
    提示 将运动方程中的参数t消去即可。@niutk

  • 第7题：

    如果输入的数据是2，3，4，则下面程序的输出应为（） PROGRAM SAM（INPUT，OUTPUT）； VAR i，x，y：integer； BEGIN FOR i：=1 TO 3 DO BEGIN Read（x）； y：=sqr（x）END； Writeln（‘x=’，x，‘y=’，y）END.

    • A、x=2 y=4 x=3 y=9 x=4 y=16
    • B、x=4 y=16 x=4 y=16 x=4 y=16
    • C、x=4 y=16
    • D、x=2 y=4 x=2 y=4 x=2 y=4

    正确答案:C

  • 第8题：

    已知x=4’b1001,y=4’0110,则x的4位补码为4’b1111，而y的4位的补码为（）


    正确答案:4’b0110

  • 第9题：

    过点（4，-1，3）且平行于直线L：（x-3）/2=y=（z-1）/5的直线方程为（）.

    • A、（x-4）/2=（y+1）/0=（z-3）/5
    • B、（x-4）/2=（y+1）/1=（z-3）/5
    • C、（x+4）/2=（y-1）/0=（z+3）/5
    • D、（x+4）/2=（y-1）/1=（z+3）/5

    正确答案:B

  • 第10题：

    单选题
    如果输入的数据是2，3，4，则下面程序的输出应为（） PROGRAM SAM（INPUT，OUTPUT）； VAR i，x，y：integer； BEGIN FOR i：=1 TO 3 DO BEGIN Read（x）； y：=sqr（x）END； Writeln（‘x=’，x，‘y=’，y）END.
    A

    x=2 y=4 x=3 y=9 x=4 y=16

    B

    x=4 y=16 x=4 y=16 x=4 y=16

    C

    x=4 y=16

    D

    x=2 y=4 x=2 y=4 x=2 y=4


    正确答案： D
    解析： 暂无解析

  • 第11题：

    单选题
    设x⊕y＝2x＋3y，x⊙y＝xy，且x、y均为正整数，若当x⊙y＝6时，x⊕y取得最小值，则x等于（　　）。
    A

    2

    B

    6

    C

    4

    D

    3


    正确答案： A
    解析：
    xy＝6，则y＝6/x；若2x＋3y最小，则2x＋18/x为最小；若使2x＋18/x最小，则2x＝18/x，得x＝3。

  • 第12题：

    单选题
    过点（4，-1，3）且平行于直线L：（x-3）/2=y=（z-1）/5的直线方程为（）.
    A

    （x-4）/2=（y+1）/0=（z-3）/5

    B

    （x-4）/2=（y+1）/1=（z-3）/5

    C

    （x+4）/2=（y-1）/0=（z+3）/5

    D

    （x+4）/2=（y-1）/1=（z+3）/5


    正确答案： A
    解析： 暂无解析

  • 第13题：

    在下列微分方程中，以函数y＝C1e^－x＋C2e^4x（C1，C2为任意常数）为通解的微分方程是（　　）。

    A． y″＋3y′－4y＝0
    B． y″－3y′－4y＝0
    C． y″＋3y′＋4y＝0
    D． y″＋y′－4y＝0

    答案：B
    解析：

    由题意知，二阶常系数齐次线性微分方程的特征方程的两个根为－1和4，只有B项满足。
    【总结】求二阶常系数齐次线性微分方程y″＋py′＋qy＝0的通解的步骤：
    ①写出微分方程的特征方程r2＋pr＋q＝0；
    ②求出特征方程的两个根r1，r2；
    ③根据r1，r2的不同情形，写出微分方程的通解：
    a．当r1≠r2，



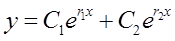
    b．当r1＝r2，



    c．一对共轭复根r1，2＝α±βi，y＝eαx（C1cosβx＋C2sinβx）。

  • 第14题：

    已知圆的方程为x2＋y2－2x＋4y＋1＝0，则圆上一点到直线3x＋4y－10＝0的最大距离为（　　）

    A.6
    B.5
    C.4
    D.3

    答案：B
    解析：

  • 第15题：

    二次函数y=x2+4x+1（　　）

    A.有最小值-3
    B.有最大值-3
    C.有最小值-6
    D.有最大值-6

    答案：A
    解析：

  • 第16题：

    下列函数中，为偶函数的是（　　）

    A.y=log2x
    B.y=x2
    C.y=4/x
    D.y=x2+x

    答案：B
    解析：

  • 第17题：

    已知∣2x-a∣≤1,∣2x-y∣≤1,则∣y-a∣的最大值为

    A.1
    B.2
    C.3
    D.4
    E.5

    答案：B
    解析：
    由三角不等式∣y-a∣=∣（2x-a）-（2x-y）∣≤∣2x-a∣+∣2x-y∣≤1+1+2

  • 第18题：

    设函数y=(x-3)4，则dy=__________．


    答案：
    解析：
    4(x-3)3dx

  • 第19题：

    已知点的运动方程为x=2t3+4，y=3t3－3，则其轨迹方程为（）

    • A、3x+4y－36=0
    • B、3x－2y－18=0
    • C、2x－2y－24=0
    • D、2x－4y－36=0

    正确答案:B

  • 第20题：

    函数y=cos2x与y=cotx的公共周期为（）

    • A、π
    • B、2π
    • C、3π
    • D、4π

    正确答案:A

  • 第21题：

    单选题
    设y＝（4x＋4）/x2－2，则曲线在拐点处的切线方程为（　　）。
    A

    y＋26/9＝－4（x＋3）/27

    B

    y＋26/9＝4（x＋3）/27

    C

    y＋26/9＝－4（x－3）/27

    D

    y＋26/9＝4（x－3）/27


    正确答案： C
    解析：
    先求方程的拐点，原方程为y＝（4x＋4）/x2－2，则有y′＝－4/x2－8/x3，y″＝8/x3＋24/x4＝8（x＋3）/x4＝0，得x＝－3。x＜－3时，y″＜0；x＞－3时，y″＞0。而y′（－3）＝－4/27，y（－3）＝－26/9，故拐点处的切线方程为y＋26/9＝－4（x＋3）/27。

  • 第22题：

    单选题
    在下列微分方程中，以y＝C1ex＋C2cos2x＋C3sin2x（C1，C2，C3为任意常数）为通解的是（　　）。
    A

    y‴＋y″－4y′－4y＝0

    B

    y‴＋y″＋4y′＋4y＝0

    C

    y‴－y″－4y′＋4y＝0

    D

    y‴－y″＋4y′－4y＝0


    正确答案： B
    解析：
    根据题设中通解的形式可知，所求齐次方程中对应的特征根为r1＝1，r2，3＝±2i。故特征方程为（r－1）（r－2i）（r＋2i）＝0即r3－r2＋4r－4＝0，则所求微分方程为y‴－y″＋4y′－4y＝0。

  • 第23题：

    单选题
    已知函数y＝y（x）在任意点x处的增量Δy＝yΔx/（1＋x2）＋a，且当Δx→0时，a是Δx的高阶无穷小，y（0）＝π，则y（1）等于（　　）。
    A

    2π

    B

    π

    C

    eπ/4

    D

    πeπ/4


    正确答案： C
    解析：
    由题意可知，dy＝[y/（1＋x2）]dx，分离变量积分得ln|y|＝arctanx＋c。又y（0）＝π得c＝lnπ，故y＝earctanx＋lnπ＝πearctanx，则y（1）＝πeπ/4。

相关内容