在一个袋中，装有五个除数字外其他完全相同的小球，球面上分别标有1、2、3、4、5这5个数字，从中任摸一个球，球面数字是奇数的概率是________．

题目
在一个袋中，装有五个除数字外其他完全相同的小球，球面上分别标有1、2、3、4、5这5个数字，从中任摸一个球，球面数字是奇数的概率是________．

相似考题

1.在一个不透明的布袋中装有2个白球和n个黄球，它们除颜色不同外，其余均相同，若从中随机摸出一球，摸到黄球的概率是4/5 ，则n=__________________.

2.（3）一个口袋内装有除颜色外其他都相同的6个白球和4个红球，从中任意摸出2个，求：A、2个都是白球的概率；B、2个都是红球的概率；C、一个白球，一个红球的概率。

3.某商店搞店庆，购物满198元可以抽奖一次。一个袋中装有编号为0到9的十个完全相同的球，满足抽奖条件的顾客在袋中摸球，一共摸两次，每次摸出一个球（球放回），如果第一次摸出球的数字比第二次大，则可获奖，则某抽奖顾客获奖概率是（ ）A．5%B．25%C．45%D．85%

4.一个口袋中装有3个一样的球，3个球上分别写有数字2，3和4。若第一次从袋子中取出一个球，记下球上的数字A，并将球放回袋中。第二次又从袋子中取出一个球，记下球上的数字B，然后算出它们的积。则所有不同取球情况所得到的积的和是。A．52B．56C．75D．81

参考答案和解析
答案：
解析：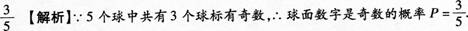
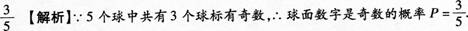
更多“在一个袋中，装有五个除数字外其他完全相同的小球，球面上分别标有1、2、3、4、5这5个数字，从中任摸一个球，球面数字是奇数的概率是________． ”相关问题

  • 第1题：

    一个口袋中装有3个一样的球，3个球上分别写有数字2，3和4。若第一次从袋子中取出一个球，记下球上的数字A，并将球放回袋中。第二次又从袋子中取出一个球，记下球上 的数字B。然后算出它们的积。则所有不同取j求情况所得到的积的和是（ ）。


    正确答案：D
    取球的情况有九种，它们的积之和为2×2+2×3+2×4+3×2+3×3+3×4+4×2+4×3+4×4=(2斗3+4)2=81。

  • 第2题：

    袋中装有大小相同的12个球，其中5个白球和7个黑球，从中任取3个球，求
    这3个球中至少有1个黑球的概率．


    答案：
    解析：
    此题利用对立事件的概率计算较为简捷，

  • 第3题：

    现有10张形状完全相同的卡片，上面分别标有1、2、3、4、5、6、7、8、9、10的数字，从中任取两张卡片，其上两数字之积为4的倍数的概率为：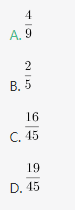


    答案：A
    解析：
    第一步，本题考查概率问题，属于基本概率。
    第二步，要使得两数字之积为4的倍数，有以下两种情况：
    （1）其中一张卡片是4，另一张卡片任选，有9种情况；
    （2）其中一张卡片是8，另一张卡片除4外任选，有8种情况；

  • 第4题：

    从1．2．3．4．5．6．7．8．9这九个数字中，随机取出一个数字，这个数字是奇数的概率是（）


    答案：B
    解析：

  • 第5题：

    一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是l，3张卡片上的数
    字是2，2张卡片上的数字是3，从盒中任取3张卡片。(1)求所取3张卡片上的数字完全相同的概率；(2)x表示所取3张卡片上的数字的中位数，求X的分布列和EX。


    答案：
    解析：

    (2)中位数X可以取1，2，3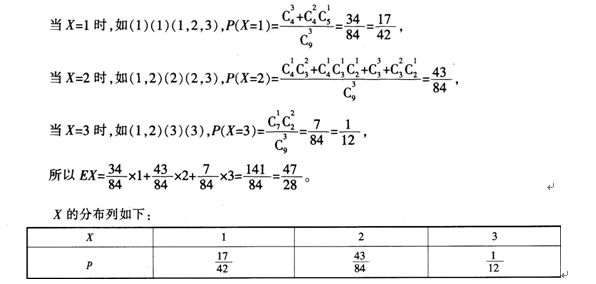

  • 第6题：

    一个骰子，六个面上的数字分别为1、2、3、3、4、5，投掷一次，向上的面出现数字3的概率是_____．


    答案：
    解析：

  • 第7题：

    A盒装有3张大小形状完全相同的卡片，分别标有数字1，2，3；B盒也装有3张大小形状完全相同的卡片，分别标有数字2，3，4。现从A，B两个盒子中各取一张卡片，对应的数字分别为a和b，记随机变量ξ=a+b，求ξ的分布列和数学期望。


    答案：
    解析：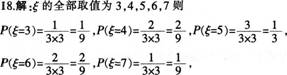


    则的分布列为


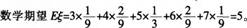
  • 第8题：

    布袋中装有1个红球，2个白球，3个黑球，它们除颜色外完全相同，从袋中任意摸出一个球，摸出的球是白球的概率是。（）

    • A、1/5
    • B、1/6
    • C、1/2
    • D、1/3。

    正确答案:D

  • 第9题：

    问答题
    35.从1，2．3，4，5中任取3个数字，则这3个数字中不含1的概率为

    正确答案：
    解析：

  • 第10题：

    单选题
    现有10张形状完全相同的卡片，上面分别标有1、2、3、4、5、6、7、8、9、10的数字，从中任取两张卡片，其上两数字之积为4的倍数的概率为：
    A

    4/9

    B

    2/5

    C

    16/45

    D

    19/45


    正确答案： C
    解析：

  • 第11题：

    单选题
    现有10张形状完全相同的卡片，上面分别标有1、2、3、4、5、6、7、8、9、10，从中任取两张卡片，其上两数字之积为4的倍数的概率为：
    A

    4/9

    B

    2/5

    C

    16/45

    D

    19/45


    正确答案： D
    解析：

  • 第12题：

    单选题
    现有10张形状完全相同的卡片，上面分别标有l、2、3、4、5、6、7、8、9、10，从中任取两张卡片，其上两数字之积为4的倍数的概率为：
    A

    4/9

    B

    2/5

    C

    16/45

    D

    19/45


    正确答案： A
    解析：

  • 第13题：

    一个袋子里装有三种不同颜色但大小相同的小球。红色小球上标有数字1，黄色小球上标有数字2，蓝色小球上标有数字3。小明从袋中摸出10个小球，它们的数字和是21，那么小明摸出的小球中最多可能有多少个小球是红色的?（ ）

    A．3个

    B．4个

    C．5个

    D．6个


    正确答案：B

  • 第14题：

    一个不透明的袋子中装有3个分别标有数字3，1，-2的球，从中随机摸出两个球，则这两个球上数字之和为负数的概率为( )。

    A.1/6
    B.1/3
    C.1/2
    D.2/3

    答案：B
    解析：
    三个数取两数随机组合有三种情况，数字之和分别为4、1、-1，则两个球上数字之和为负数的概率为1/3

  • 第15题：

    一只黑色布袋中装着分别标有数字1、2、3的三种玻璃球若干。若从布袋中随机摸出10个球，球上数字之和为21，则10个球中标有数字1的玻璃球至多有

    A.2个
    B.3个
    C.4个
    D.5个

    答案：C
    解析：
    第一步，标记“数字之和”、“之多”，考查的是常规计算问题。第二步，采用代入排除法。问的是“最多”，优先代入5，则剩余5个全为3，则总数＝5＋5×3＝20<21，排除；代入4，则剩余6个全为3，则4＋3×6＝22＞21，满足，为4个1、1个2、5个3。因此，选择C选项。

  • 第16题：

    一个袋子里面有10个球,包括红球、白球和黑球。已知从袋中任意摸一个球，得到黑球 的概率是2/5，从袋中任意摸两个球,至少有一个是白球的概率是7/9，问袋子里有多少个红球？

    a.l b.2 c.3 d.4


    答案：A
    解析：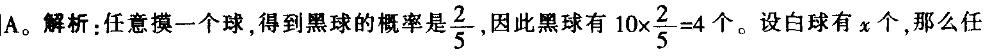

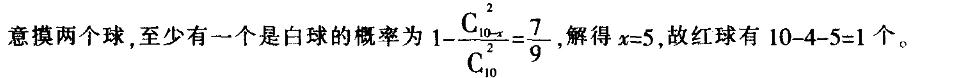
  • 第17题：

    袋子中有70个红球，30个黑球，从袋中任意摸出一个球，观察颜色后放回袋中，再摸第二个球，观察颜色后也放回袋中。

    （1）求两次摸球均为红球的概率；（3分）

    （2）求两次摸球颜色不同的概率。（4分）


    答案：
    解析：
    本题主要考查的是熟练运用分步法、分类法等方法求概率。

    通过不同事件随机发生概率进行分步分类计算。

  • 第18题：

    一个袋中装有形状大小完全相同，编号分别为1，2，3，4，5，6的六个球，现从口袋中任取两个球，则至少取到一个编号为质数的球的概率是( )。

    A.14/15
    B.4/5
    C.3/5
    D.1/2

    答案：B
    解析：

  • 第19题：

    有一个正方体，6个面上分别标有1-6这6个数字，投掷这个正方体一次，则出现向上一面的数字是偶数的概率为。（）

    • A、1/3
    • B、1/2
    • C、1/6
    • D、1/4。

    正确答案:B

  • 第20题：

    袋中有4个白球2个黑球，今从中任取3个球，则至少一个黑球的概率为（）

    • A、4/5
    • B、1
    • C、1/5
    • D、1/3

    正确答案:A

  • 第21题：

    问答题
    袋中有四个球，分别标有数字1，2，2，3，从袋中任取一球后，不放回，再取第二次，分别以X、Y记为第一次、第二次取得球上标有的数字.    求：(1)(X,Y)的分布律.　　    (2)(X,Y)的边缘分布律.　    　(3)X与Y是否独立?

    正确答案：
    解析：

  • 第22题：

    单选题
    一只盒子中有红球m个，白球10个，黑球n个，每个球除颜色外其他都相同，从中任取一个球，取得白球的概率与不是白球的概率相同，那么m与n的关系是（　　）．
    A

    m＝4，n＝6

    B

    m＝5，n＝5

    C

    m＋n＝5

    D

    m＋n＝10


    正确答案： B
    解析：
    因为从中任取一个球，取得白球的概率与不是白球的概率相同．所以白球的个数与不是白球的球的个数相等，所以m＋n＝10．

  • 第23题：

    单选题
    将号码分别为1、2、…6的6个小球放入一个袋中，这些小球仅号码不同，其余完全相同。首先，从袋中摸出一个球，号码为A.；放回后，再从此袋再摸出一个球，其号码为B.，则使不等式A.-2B.+2>0成立的事件发生的概率为：
    A

    1/6

    B

    1/4

    C

    1/3

    D

    1/2


    正确答案： C
    解析：

相关内容