在△ABC中，sinA=√2/2，tanB=√3,则该三角形的形状为()。A.锐角三角形 B.钝角三角形 C.锐角三角形或钝角三角形 D.钝角三角形或等腰三角形

题目
在△ABC中，sinA=√2/2，tanB=√3,则该三角形的形状为()。

A.锐角三角形
B.钝角三角形
C.锐角三角形或钝角三角形
D.钝角三角形或等腰三角形
相似考题

1.如b2>a2£«c2,则△ABC为()。A.锐角三角形B.直角三角形C.钝角三角形D.一般三角形

2.已知三角函数值，用计算器求锐角A，B。（1）sinA=0.6275，sinB=0.0547；（2）cosA=0.6252，cosB=0.1659；（3） tanA=0.8816，tanB=15.94 。

3.在Rt△ABC中，∠ C=90°，BC=5，sinA=0.7，求cosA，tanA的值。

4.已知三角形的一锐角为A,三边长为a,b,c其中c为斜边,则sinA=()。A、a/cB、b/cC、a/bD、b/a

更多“在△ABC中，sinA=√2/2，tanB=√3,则该三角形的形状为()。”相关问题

  • 第1题：

    在△ABC中，∠A∶∠B∶∠C＝2∶3∶4，则∠A＝________，∠C＝________.


    正确答案：
    40°、80°；

  • 第2题：

    在Rt△ABC中，A．C=90°,sin A=1/2，则∠a=________．


    答案：
    解析：

  • 第3题：

    在△ABC中，∠A=45o，∠B=30o，CD⊥AB，垂足为D，且CD=1，则⊿ABC的面积为()。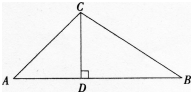

    A.（1+√3）/2
    B.（1+√3）/4
    C.(1+√6)/2
    D.(1+√6)/4

    答案：A
    解析：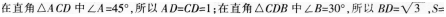

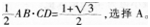
  • 第4题：

    已知三角形ABC的三个顶点的坐标分别为（0,2）、（-2,4）、（5,0）,则这个三角形的重心坐标为（ ）

    A.（1,2）
    B.（1,3）
    C.（-1,2）
    D.（0,1）
    E.（1,-1）

    答案：A
    解析：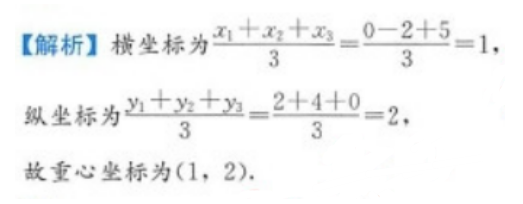

  • 第5题：

    设A(x1，y1)，B(x2，y2)，C(x3，y3)为平面上不共线的三点，则三角形ABC的面积为( )。
    A．
    B．
    C．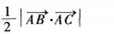
    D．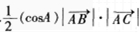


    答案：B
    解析：
    由行列式的定义展开计算可得。

  • 第6题：

    在直角三角形ABC中，点D是斜边AB的中点，点P为线段CD的中点，则( )。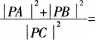

    A、2
    B、4
    C、5
    D、10

    答案：D
    解析：
    本题主要考查两点问的距离公式，以及坐标法这一重要的解题方法和数形结合的数学思

  • 第7题：

    若某三角形每个角的测角中误差为±2 秒，则该三角形角度闭合差最大不应超过（ ）。

    A、±2 秒
    B、±6 秒
    C、±2√3 秒
    D、±4√3 秒

    答案：D
    解析：
    根据误差传播定律，闭合差中误差为：√（2
    2+2 2+2 2）=2√3，最大闭合差为 2 2√3=4√3。

  • 第8题：

    如图在ΔABC中，DE∥BC，若AD：DB=1：3，DE=2，则BC等于( )。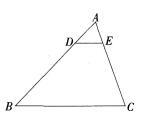

    A.8
    B.6
    C.4
    D.2

    答案：A
    解析：
    由于DE∥BC,所以DE：BC=AD：AB，又由AD:DB=1：3，所以AD：AB=1:4，由DE=2得BC=8。

  • 第9题：

    如b2＞a2＋c2，则△ABC为（）。

    • A、锐角三角形
    • B、直角三角形
    • C、钝角三1角形

    正确答案:C

  • 第10题：

    在△ABC中，若算出sinA=1/2，那么角A是多少度？


    正确答案:解：因为sinA=1／2，所以∠A=30°，或∠A=150°

  • 第11题：

    单选题
    在△ABC中，若2cosBsinA=sinC，则△ABC的形状一定是（）。
    A

    等腰直角三角形

    B

    直角三角形

    C

    等腰三角形

    D

    等边三角形


    正确答案： B
    解析： 暂无解析

  • 第12题：

    问答题
    在△ABC中，若算出sinA=1/2，那么角A是多少度？

    正确答案： 解：因为sinA=1／2，所以∠A=30°，或∠A=150°
    解析： 暂无解析

  • 第13题：

    锐角三角形ABC中，sinA=√5/5，D为BC边上的点，若△ABD 和△ACD的面积分别为2和4，过D作DE ⊥AB于E，DF⊥AC于F，


    答案：
    解析：

  • 第14题：

    在△ABC中，角A，B，C所对的边分别a，b，c。若A=π/3，

    b=2，则a=_________。


    答案：
    解析：

  • 第15题：

    如图，三角形ABC是直角三角形，S1，S2，S3为正方形，已知a，b，c分别是为，，的边长，则：（ ）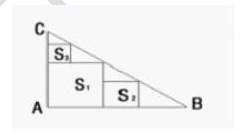

    A.a=b+c
    B.a2=b2+c2
    C.a2=2b2+2c2
    D.a3=b3+c3
    E.a3=2b3+2c3

    答案：A
    解析：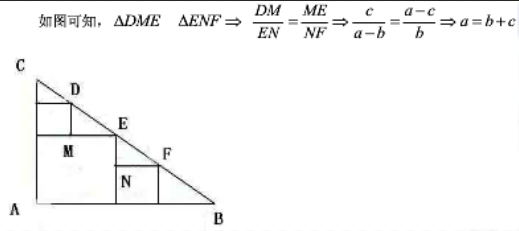

  • 第16题：

    如，在直角三角形ABC中，AC=4，BC=3，DE//BC，已知梯形BCDE的面积为3，则DE长为（ ）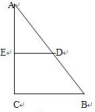



    答案：D
    解析：

  • 第17题：

    设A、B、C为欧氏平面 R2 平面上不共线的三点，则三角形ABC的面积为（ ）.


    答案：C
    解析：

  • 第18题：

    如下图，把三角形ABC 的三边分别延长1、2、3 倍，得到一个新的三角形，则新三角形的面积是原三角形ABC 面积的几倍？（ ）

    A、15
    B、16
    C、17
    D、18

    答案：D
    解析：

  • 第19题：

    在Rt△ABC中，∠C=90°，若cosA=3/5，则tanB的值是( )。

    A.3/5
    B.3/4
    C.4/5
    D.4/3

    答案：B
    解析：
    {图]

  • 第20题：

    在角形ABC中，∠C=90°，sinA=0.5，则∠B=（）。

    • A、30°
    • B、45°
    • C、60°
    • D、90°

    正确答案:C

  • 第21题：

    在△ABC中，若2cosBsinA=sinC，则△ABC的形状一定是（）。

    • A、等腰直角三角形
    • B、直角三角形
    • C、等腰三角形
    • D、等边三角形

    正确答案:C

  • 第22题：

    填空题
    在△ABC中，cosA·cosB＝0，则△ABC为____三角形．

    正确答案： 直角
    解析：
    ∵cosA·cosB＝0，∴cosA＝0，cosB≠0或cosA≠0，cosB＝0．∴∠A＝90°或∠B＝90°．∴△ABC为直角三角形．

  • 第23题：

    单选题
    下列说法正确的个数有（　　）。①等边三角形有三条对称轴；②在△ABC中，若a2＋b2≠c2，则△ABC不是直角三角形；③等腰三角形的一边长为4，另一边长9，则它的周长为17或22；④一个三角形中至少有两个锐角。
    A

    1个

    B

    2个

    C

    3个

    D

    4个


    正确答案： B
    解析：
    ①④正确。②中若a2＋b2≠c2，则△ABC也可能是直角三角形，如当∠A或∠B是直角；③若两边长为4，则4＋4＜9，不能构成三角形，故周长不能为17。

相关内容