把一个圆平均分成若干份后拼成一个近似的长方形，已知宽比长少10．7厘米，这个圆的面积是 ________ 平方厘米。(π取3．14)

题目
把一个圆平均分成若干份后拼成一个近似的长方形，已知宽比长少10．7厘米，这个圆的面积是 ________ 平方厘米。(π取3．14)

相似考题

1.要剪一个面积是12.56平方厘米的圆形纸片，至少需要面积是( )平方厘米的正方形纸片(π取3.14)。A. 12.56B. 14C. 16D. 20

2.：有一张长方体铁皮，剪下图中两个圆及一块长方形，正好可以做成1个圆柱体，这个圆柱体的底面半径为10厘米，那么原来长方形铁皮的面积是多少平方厘米？（ ）（π＝3.14）A．205.6B．1028C．1256D．2056

3.：把2米长的木棍弄断后围成一个长方形，使长比宽的2倍少O．2米，则长方形面积为（ ）。A．0．6平方米B．0．4平方米C．O．12平方米D．0．24平方米

4.圆A的半径比圆B的半径长3厘米，则可以确定圆A与圆8之间的关系为（ ）。A．面积之差为67π平方厘米B．面积之差为97π平方厘米C．周长之差为3π厘米D．周长之差为6π厘米

参考答案和解析
答案：
解析：
78．5。
由题意可知长方形的宽为圆的半径r，长为周长的一半πr,则，πr-r=-10．7，解之得r=5厘米，则这个圆的面积是πr2=78．5平方厘米。
更多“把一个圆平均分成若干份后拼成一个近似的长方形，已知宽比长少10．7厘米，这个圆的面积是 ________ 平方厘米。(π取3．14)”相关问题

  • 第1题：

    ：把2米长的木棍弄断后围成一个长方形，使长比宽的2倍少0.2米，则长方形面积为（ ）。

    A．0.6平方米

    B．0.4平方米

    C．0.12平方米

    D．0.24平方米


    正确答案：D
    设宽为x米，则2x+2×(2x-0.2)=2米，x=0.4米，长为0.6米，面积为0.4×0.6=0.24平方米。正确答案为D。

  • 第2题：

    一个长方形长与宽的比是7：4，这个长方形的长与它的周长的比是（ ）。

    A 7：11

    B 7：22

    C 22：7

    D 11：7


    正确答案：B

  • 第3题：

    一个长方形的长是宽的2倍，写出这个长方形的面积与宽之间的函数关系式。


    设:长方形的宽为x，面积为y,

        则它的长为2x,

        ∴ y=x·2x=2x²

        即面积与宽之间的函数关系式是：

         y=2x²


  • 第4题：

    用长16厘米的铁丝围成各种长方形(长、宽均为整数，且长和宽不相等)，围成最大的一个长方形面积是多少平方厘米?（ ）

    A．16

    B．15

    C．12

    D．9


    正确答案：B

    设长方形的长为a，宽为b，则这个问题就是求已知a+b=8、且a≠b时，a×b的最大值。为了便于观察，我们分析如下：
    8=1+7→1×7=7；8=2+6→2×6=12；
    8＝3+5→3×5＝15；8—4+4→4×4＝16；
    8＝5+3→5×3＝15；8＝6+2＝6×2＝12；
    8＝7+1＝7×1＝7。
    我们发现当a从小到大取值，而b从大到小取值时，a与b的积呈现这样一个变化趋势：就是先由小到大，再由大到小，中间是最大的，也就是a与b取的数越接近，它们的乘积就越大。当a—b时，a×b的值最大。由此，得出一条规律：
    如果a+b一定，只有当a—b时，a与b的乘积才最大。
    由上面的讨论可知，在a十b＝8，且a≠b中，当a＝3，b＝5时，a×b的最大值是：3×5＝15。
    所以，所围成的最大的一个长方形面积是l5平方厘米。故本题正确答案为B。

  • 第5题：

    一个正方形面积是44平方厘米,在这个正方形中作的最大的圆的面积是()平方厘米。

    A.4π

    B.11π

    C.5π

    D.7π


    正确答案：B

  • 第6题：

    如图所示，把一个半径为5cm的圆分成若干等分(左图)，剪开后拼成右图所示的图形，则该图形比原来的圆周长增加()cm。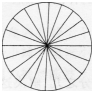


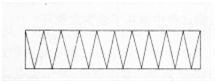    A.10
    B.5π
    C.20
    D.5π+10

    答案：A
    解析：
    拼后图形两条长(实际并不为直线)之和为原图中圆的周长，该图形的宽为原图中圆的半径，故该图形比原来圆周长增加了两条半径的长度为10cm。

  • 第7题：

    如下图所示，已知线段DE与AC平行，且与圆的半径相等，都为3厘米，0为圆的圆心。求图中阴影部分的面积。(π取3．14)


    答案：
    解析：

  • 第8题：

    一个长方形周长130厘米，如果它的宽增加1/5，长减少1/8，就得到一个相同周长的新长方形，则原长方形的面积为多少平方厘米：
    A 1000
    B 900
    C 850
    D 840


    答案：A
    解析：

  • 第9题：

    一个长方形的长与宽的比是14：5，如果长减少l3厘米，宽增加l3厘米，则面积增加182平方厘米，那么原长方形面积是多少平方厘米?

    A.448
    B.630
    C.812
    D.1120

    答案：B
    解析：
    设原长方形的长为l4a，宽为5a，由题意可得，(14a一l3)x(5a+13)=14a×5a+182，解得a=3，
    原长方形面积是14×3×5×3=630平方厘米，应选择8。

  • 第10题：

    老师利用幻灯片向学生演示将一个圆切分成若干等份，并通过剪拼成近似的长方形。这时幻灯片主要表现的是媒体的（）特征。

    • A、重现力
    • B、表现力
    • C、传播力
    • D、可控力

    正确答案:C

  • 第11题：

    九个边长分别为1，4，7，8，9，10，14，15，18的正方形可以拼成一个长方形，问这个长方形的长和宽是（）。


    正确答案:33和32

  • 第12题：

    单选题
    一个正方形与这个正方形内最大的圆的周长的比是（）。（π≈3.14）
    A

    1：3.14

    B

    157：200

    C

    200：157


    正确答案： C
    解析： 暂无解析

  • 第13题：

    一个长方形铁锭，底面周长为32厘米，长与宽的比是3︰1，高比宽短30%。用它刚好可以铸成高为6厘米的圆锥体，那么圆锥体的底面积为（ ）平方厘米。

    A．67.2

    B．201.6

    C．537.6

    D．1612.8


    正确答案：A
    先求出长方体的长、宽、高。

  • 第14题：

    ：一个长方形的操场，周长是270米，长与宽的比是5：4，这个操场的面积是（ ）平方米。

    A．1000

    B．370

    C．4500

    D．15000


    正确答案：C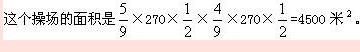

  • 第15题：

    一个长方形的长减少5cm，宽增加2cm，就成为一个正方形，并且这两个图形的面积相等。这个长方形的长、宽各是多少

  • 第16题：

    一个正方体和一个长方体拼成一个新的长方体，拼成的长方体的表面积比原来的长方体的表面积增加了50平方米。原来正方体的表面积是多少平方厘米?


    正确答案：750000平方厘米

  • 第17题：

    用长16厘米的铁丝围成各种长方形（长、宽均为整数，且长和宽不相等），围成的最大的一个长方形的面积是多少平方厘米？（ ）

    A. 16
    B. 15
    C. 12
    D. 9

    答案：B
    解析：
    设长方形的长为a，宽为b，则这个问题就是求已知a+b=8、且a≠b时，axb的最大值。为了便于观察，我们分析如下：
    8 = 1 + 7→1X7=7；8 = 2 + 6→2X6 = 12；
    8 = 3 + 5→3 X5=15；8 = 4 + 4→4 X 4 = 16；
    8 = 5 + 3→5X3=15；8 = 6 + 2 → 6X2 = 12；
    8 = 7 + 1→ 7X1=7。
    我们发现当a从小到大取值，而b从大到小取值时，a与b的积呈现这样一个变化趋势：就是先由小到大，再由大到小，中间是最大的，也就是a与b取的数越接近，它们的乘积就越大。当a = b时，aXb的值最大。由此，得出一条规律：
    如果a+b—定，只有当a =b时，a与b的乘积才最大。
    由上面的讨论可知，在a +b=8，且a≠b中，当a=3，b= 5时，aXb的最大值是：3X5 = 15。 所以，所围成的最大的一个长方形的面积是15平方厘米。故本题正确答案为B。

  • 第18题：

    如图，由四个全等的小长方形拼成一个大正方形，每个长方形的面积都是1，且长与宽之比大于等于2，则这个大正方形的面积至少为 ()。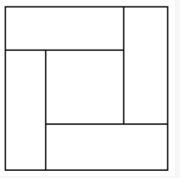

    A.3
    B.4.5
    C.5
    D.5.5

    答案：B
    解析：
    第一步，本题考查几何问题，属于其他几何类。
    第二步，大正方形的面积＝小长方形面积×4＋中间小正方形的面积，由于每个长方形的面积都确定为1，那么要使大正方形的面积最小，则应使中间小正方形的面积最小。
    第三步，设长方形的长为x，宽为y，则中间小正方形的边长为x－y，面积为（x－y）2，由条件可知x≥2y，那么当x＝2y时，中间小正方形的面积（x－y）2最小，大正方形的面积也为最小。已知每个长方形的面积都为1，那么

    第四步，大正方形的面积＝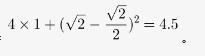

    因此，选择B选项。

  • 第19题：

    如图所示，长方形卡纸的长为33．12cm，利用图中的阴影部分正好能做成一个圆柱体(接头忽略不计，π取3．14)。则这个圆柱体的表面积为______。


    答案：
    解析：
    502．4cm2。解析：设该圆柱体的半径为r，则2r+2πr=33．12，解得r=4，圆柱的高h=4r=16，故该圆柱均表面积S=2πr2+2πrh=502．4cm2。

  • 第20题：

    若将一个长为8厘米、宽为6厘米的长方形盖在一个圆上，两个图形重叠部分的面积占圆的三分之二，占长方形面积的一半。则这个圆的面积为多少平方厘米？

    A. 64
    B. 24
    C. 48
    D. 36

    答案：D
    解析：
    根据题意，重叠部分的面积等于长方形面积的一半，所以重叠部分的面积为8×6÷2＝24，又重叠部分的面积占圆的2/3，所以圆的面积为24÷2/3＝36.因此，本题答案选择D选项。
    技巧
    公式法

  • 第21题：

    小学数学《圆的面积》

    一、考题回顾



    二、考题解析
    【教学过程】
    (一)创设情景，导入新课
    一只小狗被它的主人用一根长1米的绳子栓在草地上，问小狗能够活动的范围有多大?
    问题：1.小狗能够活动的最大面积是一个什么图形?
    2.如何求圆的面积呢?
    (二)师生互动，探索新知
    (1)引导：平行四边形面积可以转化成长方形面积，那么是否可以将圆转化成已学的图形呢?
    (2)实验操作：教师将课前准备好的圆分给各小组(前后四人为一组)。请同学们试试看，是否可以将圆转化成为长方形。
    (3)动画展示：
    把圆分成4份、8份，然后拼图。



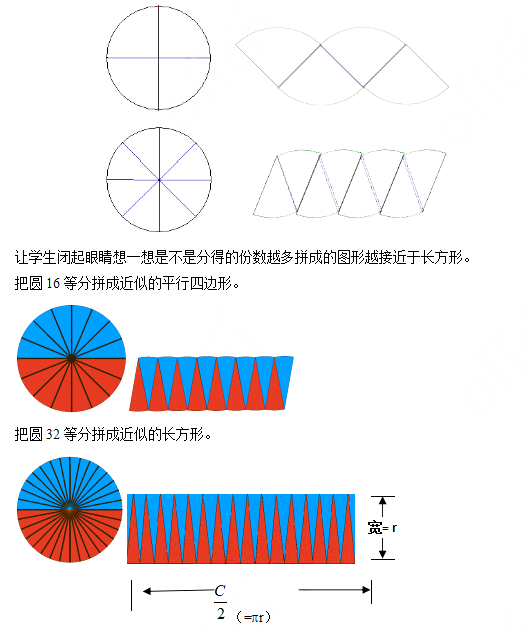
    ①拼成的平行四边形的高相当于圆的半径，它的底相当于圆周长的一半。
    ②拼成的长方形的宽相当于圆的半径，长相当于圆周长的一半。
    当我们把圆平均分得的份数越多，拼成的图形就越接近于一个长方形，它的面积也就越接近了这个长方形的面积。
    (4)得出结论：
    问1：既然圆的面积无限接近于长方形。那么我们如何根据长方形的面积来推导圆的面积公式呢?
    问2：长方形的长、宽与圆有什么关系呢?
    再次展示动画。



    1.简单说一说引导学生学习圆的面积?
    2.对于圆的面积公式的推导过程体现了数学中的哪种思想方法?


    答案：
    解析：
    1.
    本节课主要是激发学生原有知识经验，促进正迁移，实现圆面积公式的推导。例如新课一开始，就可围绕“怎样计算一个圆的面积呢”引导学生回忆已学过的一般图形的面积的含义，促进对圆面积概念的理解。同时，再引导学生回顾以前研究的多边形面积时，我们是采取怎样的办法，将多边形转化为已学的图形来求面积，为学生学习圆面积公式的推导提供思维策略的支撑。在此基础上提出“是否也可以把圆转化为已学的图形呢?”，后续的教学便顺理成章，水到渠成，有利于学生展开自主探索、合作交流，进而抽象概括归纳出圆的面积公式。
    2.
    转化、极限的思想方法。

  • 第22题：

    老师利用幻灯片向学生演示将一个圆切成若干等份，并通过剪拼成近似的长方形，这时幻灯片主要表现的是的（）特征。

    • A、重现力
    • B、表现力
    • C、传播力
    • D、可控性

    正确答案:B

  • 第23题：

    一个正方形与这个正方形内最大的圆的周长的比是（）。（π≈3.14）

    • A、1：3.14
    • B、157：200
    • C、200：157

    正确答案:C

相关内容