若直线ax+y+5=0，与直线x-2y+7=0垂直，则a的值为______ 。

题目
若直线ax+y+5=0，与直线x-2y+7=0垂直，则a的值为______ 。

相似考题

1.两个变量(x，y)，其观测值为，(x1，y1)(z2，Y2)，2，…，n，若回归方程为，y＝a+bx则下列表述正确的是( )。A．回归直线经过点(0，0)B．回归直线经过点C．回归直线经过点(1，a)D．以上都不正确

2.设平面方程为x+y+z+1=0，直线方程为1－x=y+1=z，则直线与平面： A.平行 B.垂直 C.重合 D.相交但不垂直

3.已知某瞬时平面图形上O点的加速度为a0。图形的角速度ω=0，角加速度为α0。则图形上过O点并垂直于a0的直线mn上各点加速度的方向应是( )。A.指向O点 B.垂直mn直线 C.与mn直线成θ角 D.沿mn直线背离O点

4.若所有观察值都落在回归直线上,则x与y之间的相关系数是( )。A.r = 0B.r = 1C.－1 若所有观察值都落在回归直线上，则x与y之间的相关系数是（ ）。A.r = 0B.r = 1C.-1D.0

更多“若直线ax+y+5=0，与直线x-2y+7=0垂直，则a的值为______ 。 ”相关问题

  • 第1题：

    设平面方程x+y+Z+1=0，直线的方程是l-x=y+1= z，则直线与平面：
    (A)平行 （B)垂直 (C)重合 (L)相交但不垂直


    答案：D
    解析：
    解：选D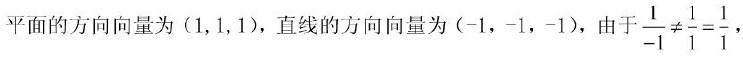
    所以直线与平面不垂直。又1x(-1) + 1x1+1x1=1≠0，所以直线与平面不平行。

  • 第2题：

    已知平面π过点(1，1，0)、(0，0，1)、(0，1，1)，则与平面π垂直且过点(1，1，1)的直线的对称方程为 ( )。



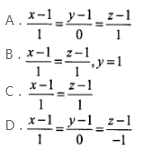    答案：B
    解析：
    平面π的法向量所求直线的方向向量为i+k，故应选B。@##

  • 第3题：

    若直线l1：(a+1)x+a2y-3=0与直线l2：2x+ay一2a-1=0平行，则a=_______。


    答案：
    解析：

  • 第4题：

    若所有观察值都落在回归直线上，则x与y之间的相关系数是（　）。

    A.r=0
    B.r=1
    C.-1<1
    D.0<1

    答案：B
    解析：

  • 第5题：

    当供给曲线为（ ），供给弹性等于（ ） 。

    A.垂直线，无限大
    B.垂直线，0
    C.水平线，1
    D.水平线，0

    答案：B
    解析：
    此时，任何价格所对应的供给都是相同的，因此，根据供给弹性计算公式，供给弹性等于0.

  • 第6题：

    设直线的方程为x=y-1=z， 平面的方程为x-2y+z=0，则直线与平面（ ）。
    A.重合 B.平行不重合 C.垂直相交 D.相交不垂直


    答案：B
    解析：
    正确答案为B。
    提示：直线的方向向量为s = (1，1，1)，平面的法向量为n= (1，-2，1)，s·n = 1-2 + 1 = 0,这两个向量垂直，直线与平面平行，又直线上的点(0，1，0)不在平面上，故直线与平面不重合。

  • 第7题：

    点沿其轨迹运动时（）

    • A、若aτ=0，an≠0则点作变速曲线运动；
    • B、若aτ=常量、an≠0，则点作匀变速曲线运动；
    • C、若aτ≠0、an=0，则点作变速曲线运动；
    • D、若aτ≠0、an=0，则点作匀速直线运动。

    正确答案:B

  • 第8题：

    设直线的方程为x=y-1=z，平面的方程为x-2y+z=0，则直线与平面（）。

    • A、重合
    • B、平行不重合
    • C、垂直相交
    • D、相交不垂直

    正确答案:B

  • 第9题：

    单选题
    如果估计标准误差Syx=0，则表明（）。
    A

    全部观察值和回归值都不相等

    B

    回归直线代表性小

    C

    全部观测值与回归值的离差之积为0

    D

    全部观察值都落在回归直线上


    正确答案： D
    解析： 暂无解析

  • 第10题：

    单选题
    设直线方程为x=y-1=z，平面方程为x-2y+z=0，则直线与平面（　　）。[2011年真题]
    A

    重合

    B

    平行不重合

    C

    垂直相交

    D

    相交不垂直


    正确答案： C
    解析：
    直线的方向向量s＝（1，1，1），平面的法向向量n＝（1，－2，1），其向量积s·n＝1－2＋1＝0，则这两个向量垂直，即直线与平面平行。又该直线上的点（0，1，0）不在平面上，故直线与平面不重合。

  • 第11题：

    多选题
    因为回归直线是根据回归方程所求得，所以必然出现下列情况（）
    A

    回归直线必然通过点（'X，'Y）

    B

    当X为任何数时，均可在回归直线上找到相应的Y值

    C

    当a大于0时，回归直线与纵轴相交处，Y值必为正值

    D

    当a大于0时，回归直线与纵轴相交处，Y值必为负值

    E

    当b等于0时，回归直线与横轴重合


    正确答案： C,A
    解析： 暂无解析

  • 第12题：

    单选题
    已知直线，mx＋4y－2＝0与2x－5y＋n＝0互相垂直，垂足为（1，P），则m—n＋P的值为（　　）
    A

    24

    B

    20

    C

    0

    D

    －4


    正确答案： B
    解析：
    由两直线垂直的斜率关系可得m＝10，直线方程为5x＋2y－1＝0和2x－5y＋n＝0，当x＝1时，y＝－2，即P＝－2，将交点代入2x－5y＋n＝0得n＝－12，因此m—n＋P＝20．

  • 第13题：

    设直线方程为x=y-1=z，平面方程为x-2y+z=0，则直线与平面：
    A.重合 B.平行不重合
    C.垂直相交 D.相交不垂直


    答案：B
    解析：
    从而知直线//平面或直线与平面重合；再在直线上取一点（0,1,0），验证该点是否满足平面方程。

  • 第14题：

    设平面方程:x + y + z-1 = 0，直线的方程是1-x = y + 1=z，则直线与平面：
    A.平行 B.垂直 C.重合 D.相交但不垂直


    答案：D
    解析：

  • 第15题：

    对于直线回归方程y=bo+bx，以下说法正确的是( )。

    A.截距b0＞0，表示回归直线与纵轴的交点在原点下方
    B.截距b0＜0，表示回归直线与纵轴的交点在原点下方
    C.截距bo=0，表示回归直线通过原点
    D.b=0，表示回归直线平行于x轴
    E.b=0，表示回归直线垂直于x轴

    答案：B,C,D
    解析：
    截距bo＞0，表示回归直线与纵轴的交点应当在原点上方。b=o，表示回归直线平行于x轴，即y与x无线性依存关系。

  • 第16题：

    已知平面π过点M1(1，1，0)，M2(0，0，1)，M3(0，1，1)，则与平面π垂直且过点(1，1，1)的直线的对称方程为：



    答案：A
    解析：
    提示 求出过M1，M2，M3三点平面的法线向量。



    @##

  • 第17题：

    若曲线y=χ4的一条切线I与直线χ+4y-8=0垂直，求切线I的方程。


    答案：
    解析：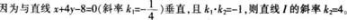

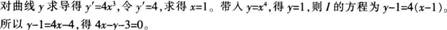
  • 第18题：

    已知平面π过点(1,1，0)、(0,0,1), (0,1,1),则与平面π垂直且过点(1,1,1)的直线的对称式方程为（ ）。


    答案：B
    解析：
    正确答案是B。
    提示：平面π的法向量，所求直线的方向向量为i+k ,故应选B。

  • 第19题：

    因为回归直线是根据回归方程所求得，所以必然出现下列情况（）

    • A、回归直线必然通过点（'X，'Y）
    • B、当X为任何数时，均可在回归直线上找到相应的Y值
    • C、当a大于0时，回归直线与纵轴相交处，Y值必为正值
    • D、当a大于0时，回归直线与纵轴相交处，Y值必为负值
    • E、当b等于0时，回归直线与横轴重合

    正确答案:A,C

  • 第20题：

    如果估计标准误差Syx=0，则表明（）。

    • A、全部观察值和回归值都不相等
    • B、回归直线代表性小
    • C、全部观测值与回归值的离差之积为0
    • D、全部观察值都落在回归直线上

    正确答案:D

  • 第21题：

    填空题
    若ab＜0，且bc＜0，则直线ax＋by＋c＝0必不经过第____象限．

    正确答案： 四
    解析：
    由ab＜0可知，直线斜率大于零，直线的倾斜角为锐角，由bc＜0可知，直线与y轴交点在正半轴，由以上推论可以画出直线的大致图形，可知直线不经过第四象限．

  • 第22题：

    填空题
    直线（3a＋2）x＋（1－4a）y＋8＝0与（5a－2）x＋（a＋4）y－7＝0互相垂直，则a的值为____.

    正确答案： 0或1
    解析：
    根据两条直线垂直的充要条件，有（3a＋2）（5a－2）＋（1－4a）（a＋4）＝0，解方程得：a＝0或a＝1．

  • 第23题：

    单选题
    设直线的方程为x=y-1=z，平面的方程为x-2y+z=0,则直线与平面（ ）
    A

    重合

    B

    平行不重合

    C

    垂直相交

    D

    相交不垂直


    正确答案： C
    解析：

相关内容