如果曲线Y=f(x)在点(x,y)处的切线斜率与x2成正比,并且此曲线过点(1,-3)和(2,11),则此曲线方程为( ).A.Y=3-2 B.Y=2x3-5 C.Y=x2-2 D.Y=2x2-5
题目
B.Y=2x3-5
C.Y=x2-2
D.Y=2x2-5
相似考题
更多“如果曲线Y=f(x)在点(x,y)处的切线斜率与x2成正比,并且此曲线过点(1,-3)和(2,11),则此曲线方程为( ).”相关问题
-
第1题:
曲线y=x3—2x在点(1,-1)处的切线方程为 .
正确答案:
y=x-2【考情点拨】本题主要考查的知识点为切线方程.【应试指导】 -
第2题:
函数y=x²+x-2,已知该曲线在点M处的切线斜率为3,则点M的坐标是(2,0)。()此题为判断题(对,错)。
参考答案:错误
-
第3题:
如果曲线y=f(x)在点(x,y)处的切线斜率与x2成正比,并且此曲线过点(1,-3)和(2,11),则此曲线方程为( )。
A. y=x3-2
B. y=2x3-5
C. y=x2-2
D. y=2x2-5
正确答案:B由曲线过点(1,-3)排除A、C项。由此曲线过点(2,11)排除D,故选B。y=2x3-5显然过点(1,-3)和(2,11),且它在(x,y)处的切线斜率为6x2,显然满足与x2成正比。
-
第4题:
曲线y=e-x在点(0,1)处的切线斜率k=______.答案:解析:
-
第5题:
设曲线y=x2+x-2在点M处切线的斜率为2,则点M的坐标为().答案:解析:
【考情点拨】本题考查了曲线上一点处的切线的知识点.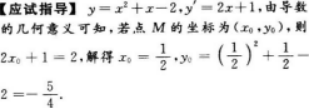
-
第6题:
曲线y=sin(x+1)在点(-1,0)处的切线斜率为______.答案:解析:填1.因为y'=cos(x+1),则y'(-1)=1. -
第7题:
曲线y=x3-x在点(1,0)处的切线方程y=______.答案:解析:填2(x-1).因为y'=3x2-1,y'(1)=2,则切线方程为y=2(x-1). -
第8题:
曲线y=x3-4x+2在点(1,-1)处的切线方程为( )A.x-y-2-0
B.x-y=0
C.x+y=0
D.x+y-2=0答案:C解析: -
第9题:
已知曲线y=x2+x-2的切线ι斜率为3,则ι的方程为_________.答案:解析:【答案】3x-y-3=0【考情点拨】本题考查了切线的知识点.
-
第10题:
曲线x2=6y-y3在(-2,2)点切线的斜率为()
正确答案:2/3 -
第11题:
填空题曲线x2=6y-y3在(-2,2)点切线的斜率为()正确答案: 2/3解析: 暂无解析 -
第12题:
单选题函数y=f(x)是由方程xy+2lnx=y4所确定,则曲线y=f(x)在点(1,1)处的切线方程为( )。Ax-y=0
Bx+y=0
C-x-y=0
D-x+y=0
正确答案: C解析:
xy+2lnx=y4两端对x求导,得y+xy′+2/x=4y3·y′。x=1时,y=1,y′(1)=1,则切线方程为y-1=x-1,即x-y=0。 -
第13题:
曲线y=x2+1在点(1,2)处的切线方程为__________.
正确答案:
y=2x -
第14题:
已知曲线y=x3-3x2-1,过点(1,-3)作其切线,求切线方程。
正确答案:y′=3x2-6x,当x=1时,y=1-3-1=-3,即点(1,-3)在曲线上。可知此切线的斜率为k=3×12-6×1=-3,由点斜式可知,此切线的方程为y-(-3)=-3(x-1)即为y=-3x。
-
第15题:
设曲线y=^e1?x2与直线x=-1的交点为P,则曲线在点P处的切线方程是( )A.2x-y+2=0
B.2x+y+1=0
C.2x+y-3=0
D.2x-y+3=0答案:D解析:
@## -
第16题:
曲线x2+y2=2x在点(1,1)处的切线方程为.答案:解析:【答案】y=1【考情点拨】本题考查了曲线上一点处的切线方程的知识点.
【应试指导】由x2+y2=2x,两边对x求导得2x+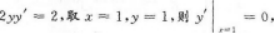
-
第17题:
曲线y=ex+x2在点(0,1)处的切线斜率为______.答案:解析: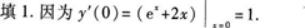
-
第18题:
曲线y=2x2在点(1,2)处的切线方程y=______.答案:解析: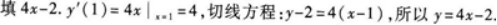
-
第19题:
设函数f(x)具有2阶连续导数,若曲线y=f(x)过点(0,0)且与曲线y=^x在点(1,2)处相切,则 =________.答案:1、2(ln2-1)解析:
=________.答案:1、2(ln2-1)解析:
-
第20题:
曲线y=3x+1在点(1,3)处的切线方程为( )。A、y=2x+1
B、r=4x-1
C、y=4x+2
D、y=3x答案:B解析:先求出y=x3+1在点(1,3)处切线的斜率为4,再根据过(1,3),得到切线方程为y=4x-l。 -
第21题:
设y=f(x)可导,点a0=2为f(x)的极小值点,且f(2)=3,则曲线y=f(x)在点(2,3)处的切线方程为______.答案:解析:由于y=f(x)可导,点x0=2为f(x)的极小值点,由极值的必要条件可知f′(2)=0.曲线y=fx)在点(2,3)处的切线方程为y-3=f′(2)(x-2)=0,即y=3为所求切线方程. -
第22题:
填空题函数y=f(x)是由方程xy+2lnx=y4所确定,则曲线y=f(x)在点(1,1)处的切线方程为____。正确答案: x-y=0解析:
xy+2lnx=y4两端对x求导,得y+xy′+2/x=4y3·y′。x=1时,y=1,y′(1)=1,则切线方程为y-1=x-1,即x-y=0。 -
第23题:
单选题函数y=f(x)是由方程xy+2lnx=y4所确定,则曲线y=f(x)在点(1,1)处的切线方程为( )。A-x-y=0
Bx-y-1=0
Cx-y=0
Dx+y=0
正确答案: A解析:
xy+2lnx=y4两端对x求导,得y+xy′+2/x=4y3·y′。x=1时,y=1,y′(1)=1,则切线方程为y-1=x-1,即x-y=0。
