锐角三角形ABC中，sinA=√5/5，D为BC边上的点，若△ABD 和△ACD的面积分别为2和4，过D作DE ⊥AB于E，DF⊥AC于F，

题目
锐角三角形ABC中，sinA=√5/5，D为BC边上的点，若△ABD 和△ACD的面积分别为2和4，过D作DE ⊥AB于E，DF⊥AC于F，

相似考题

1.△ABC中，AB=3，BC=4，则AC边的长满足（ ）。A．AC=5B．AC>1C．AC<7D．1<AC<7

2.△ABC中，AB=13cm，BC=10cm，BC边上的中线AD=12cm.求AC

3.对边相等,对角相等的凸四边形,是平行四边形吧?方法①∠B小于90°；左上为A，左下为B，右下为C，右上为D；已知∠B=∠D；AB=CD;证明：过A作AN⊥BC于N； 过C作CM⊥AD于M； 连接AC∵AN⊥BC；CM⊥AD∴∠ANB=∠DMC=90°又∵∠B=∠D；AB=CD∴△ANB=△DMC(AAS）∴AN=CM;BN=DM又∵∠ANB=∠DMC=90°，AC=AC∴△ACD=△AMD（HL）∴AM=DN又∵BN=DM∴BD=AC∵BD=AC；AB=CD∴凸四边形ABCD为平行四边型。方法②∠B大于90°左上为A，左下为B，右下为C，右上为D；已知∠B=∠D；AB=CD;证明：延长CD,过A作AN⊥BC于N； 延长AB,过C作CM⊥AD于M； 连接AC∵AN⊥BC；CM⊥AD∴∠ANB=∠DMC=90°又∵∠B=∠D；AB=CD∴△ANB=△DMC(AAS）∴AN=CM;BN=DM又∵∠ANB=∠DMC=90°，AC=AC∴△ACD=△AMD（HL）∴AM=DN又∵BN=DM∴BD=AC∵BD=AC；AB=CD∴凸四边形ABCD为平行四边型。方法③∠B等于90°证明：∵∠B=∠D=90°；AB=CD；AC=AC∴△ABC=△ADC（HL）∴AB=CB∵BD=AC；AB=CD∴凸四边形ABCD为平行四边型。有错吗？若我的证明有错请明示，我知道有个反例，但它是凹四边形。

4.某工序过程有六个因子A、B、C、D、E、F,工程师希望做部分因子试验确定主要的影响因素,准备采用26－2设计,而且工程师根据工程经验判定AB、BC、AE、DF之间可能存在交互作用,但是MINITAB给出的生成元(Generators)为E=ABC,F=BCD,为了不让可能显着的二阶交互作用相互混杂,下列生成元可行的是:()A.E=ABD，F=ABDB.E=ABD，F=BCDC.E=ABC，F=ACDD.E=ACD，F=ACD

更多“锐角三角形ABC中，sinA=√5/5，D为BC边上的点，若△ABD 和△ACD的面积分别为2和4，过D作DE ⊥AB于E，DF⊥AC于F， ”相关问题

  • 第1题：

    设关系模式R(A，B，C，D，E)，F是R上成立的FD集，F={AB→C，BC→A，AC→B，D→ E }，R的候选键为(1)。

    A．ABC、ACD、ACE

    B．ABD、BCD、ACD

    C．ABC、BCD、ACD

    D．ABD、ACD、ACE


    正确答案：B
    解析：模式R有三个候选键：ABD、BCD、ACD三个。推导过程如下：①从AB→C和D→E，可推出ABD→ABCDE。②从BC→A和D→E，可推出BCD→ABCDE。③从AC→B和D→E，可推出ACD→ABCDE。

  • 第2题：

    在△ABC中，D、E分别是边AB、AC的中点，若BC＝5，则DE的长是（ ）。

    A．2.5

    B．5

    C．10

    D．15


    正确答案：A
    分析：由D、E分别是边AB、AC的中点可知，DE是ABC的中位线，根据中位线定理可知，DE＝BC＝2.5。
    涉及知识点：中位线
    点评：本题考查了中位线的性质，三角形的中位线是指连接三角形两边中点的线段，中位线的特征是平行于第三边且等于第三边的一半。
    推荐指数：★★

  • 第3题：

    如图⊙O和⊙O’相交于A，B两点，过A作两圆的切线分别交两圆于C，D两点，连接DB并延长交⊙O于点E.证明：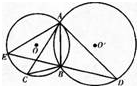

    (1)AC?BD=AD?AB；
    (2)AC=AE.


    答案：
    解析：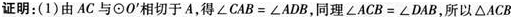


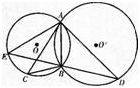
  • 第4题：

    在△ABC中，已知AB＝5，AC＝3，∠A＝120°，则BC长为



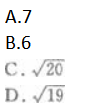    答案：A
    解析：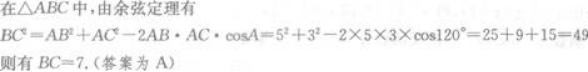

  • 第5题：

    在△ABC中，AB=2，BC=3，B=60°．求AC及△ABC的面积．


    答案：
    解析：
    解：由余弦定理得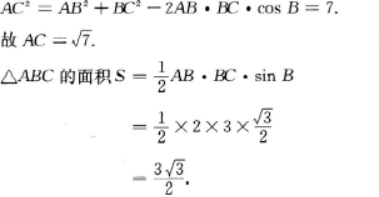

  • 第6题：

    如，在直角三角形ABC中，AC=4，BC=3，DE//BC，已知梯形BCDE的面积为3，则DE长为（ ）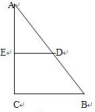



    答案：D
    解析：

  • 第7题：

    如图1，在△ABC中，BC = 8 cm，AB的垂直平分线交AB于点Ｄ， 交边AC于点E，△BCE的周长等于18 cm，则AC的长等于（ ）

    A、6cm　
    B、8cm
    C、10cm　　
    D、12cm

    答案：C
    解析：

  • 第8题：

    下列判断中，哪些属于假言判断（）

    • A、正多面体只有5种
    • B、两点之间的距离，线段最短
    • C、如果a+b=1，那么ab至少有一个为11/2
    • D、若中△ABC'∠C=900，则AB2+BC2=AC2
    • E、X＞1

    正确答案:C,D

  • 第9题：

    已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC，BC为直径作半圆，面积分别记为S1和S2，则S1+S2的值等于4π。


    正确答案:错误

  • 第10题：

    在一个试验设计问题中，共需要考查7个因子A、B、C、D、E、F和G，但经费所限最多只能进行20次试验（中心点在内）。此实际问题要求，除7个因子的主效应必须估计之外，还必须估计出AB、AC、BE、CF共4个二阶交互效应。问：下列哪个生成元的选择是可行的（）？

    • A、E=ABC，F=ABD，G=ACD
    • B、E=ACD，F=ABC，G=BCD
    • C、E=ABD，F=BCD，G=ABC
    • D、E=ABD，F=ACD，G=ABC

    正确答案:C

  • 第11题：

    单选题
    某工艺条件试验中有六个因子A、B、C、D、E、F，试验人员希望做部分因子试验考察各主效应和AD、AC、BC、DF四个二阶交互效应是否显著，准备采用26-2+4设计，但是MINITAB给出的生成元（Generators）为E=ABC，F=BCD，为了不让可能显著的二阶交互作用相互混杂，下列生成元正确的是：（）
    A

    E=ABD、F=BCD

    B

    E=BCD、F=ABC

    C

    E=ACD、F=BCD

    D

    E=ABD、F=ACD


    正确答案： B
    解析： 暂无解析

  • 第12题：

    单选题
    在一个试验设计问题中，共需要考查7个因子A、B、C、D、E、F和G，但经费所限最多只能进行20次试验（中心点在内）。此实际问题要求，除7个因子的主效应必须估计之外，还必须估计出AB、AC、BE、CF共4个二阶交互效应。问：下列哪个生成元的选择是可行的（）？
    A

    E=ABC，F=ABD，G=ACD

    B

    E=ACD，F=ABC，G=BCD

    C

    E=ABD，F=BCD，G=ABC

    D

    E=ABD，F=ACD，G=ABC


    正确答案： D
    解析： 暂无解析

  • 第13题：

    设X=ab，Y=cd分别为2位二进制正整数，x＞Y的逻辑表示式是( )。

    A．ac+abd+bcd

    B．ac+adb+bcd

    C．ad+abc+bcd

    D．ac+bcd+abd


    正确答案：D

  • 第14题：

    如图：已知圆0，点P在圆外，D，E在圆上，PE交圆于C，PD与圆相切，G为CE上一点且满足PG=PD,连接DG并延长交圆于A，作弦AB⊥EP，垂足为F。

    (1)求证：AB为圆的直径；
    (2)若AC=BD，AB=5，求弦DE的长。


    答案：
    解析：
    (1)证明：∵PG=PD,∴∠PGD=∠PDG，又∵∠AGF=∠PGD，∠PDG=∠ABD，∴∠AGF=∠ABD，∴∠ADB=∠AFP=90°，∴AB为圆的直径。

  • 第15题：

    平行四边形ABCD如右图所示，E为AB上的一点，F、G分别是AC和DE、DB的交点。若AB=3AE，则四边形BEFG与ABCD的面积之比是：

    A.2︰7
    B.3︰13
    C.4︰19
    D.5︰24

    答案：D
    解析：
    第一步，本题考查几何问题，属于平面几何类，用赋值法解题。
    第二步，题干没给出具体数值，可以采用赋值法解题。赋值AB=3，平行四边形ABCD的高为4，则AE=1；由于△AEF相似于△CDF，则两个三角形的高之比为AE：DC=1︰3，可知△AEF的高为
    4*1/4=1。△ABG与△CDG全等，则△ABG的高为4÷2=2。
    第三步，四边形BEFG面积=△ABG面积-△AEF面积=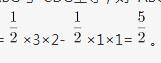

    四边形ABCD面积=3×4=12，两者之比为 ︰12=5︰24。
    因此，选择D选项。

  • 第16题：

    在△ABC中，AB=2，BC=3，B=60°，BD为AC边上的高．求AC，BD．


    答案：
    解析：

  • 第17题：

    如图6-9所示,在△ABC中,AD⊥BC于D点,BD=CD,若BC=6,AD=5,则图中阴影部分的面积为（ ）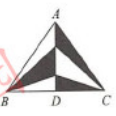

    A.3
    B.7.5
    C.15
    D.30
    E.5.5

    答案：B
    解析：

  • 第18题：

    已知△ABC的三边长AC＝3，BC＝4，AB＝5，P为AB边上任意一点，则CP→ (BA→－BC→)的最大值为(　　)

    A、8
    B、9
    C、12
    D、15

    答案：B
    解析：

  • 第19题：

    分别用分析法，综合法证明如下命题。
    命题：如图：三角形ABC的角B和角C的角平分线相交于点0，过点O作平行于底边BC的直线，交AB边于点D，交AC边于点E，则DE=BD+EC。



    答案：
    解析：
    证明：(1)分析法证明：要证DE=BD+EC．
    需证OD=BD，OE=CE，
    需证∠DBO=∠DOB,∠ECO=∠EOC，
    显然由已知OB为∠DBC的平分线，OC为∠ECB的平分线，且DE∥BC，所以∠DBO=∠DOB,∠ECO=∠EOC,所以命题成立。
    (2)综合法证明：
    ∵OB为∠DBC的平分线，OC为1ECB的平分线，且DE∥BC，
    ∴∠DBO=∠OBC=∠DOB,∠EC0=∠BC0=∠EOC,
    ∴BD=OD．EC=OE。
    又∵DE=OD+DE
    ∴DE=BD+EC。

  • 第20题：

    若正方形ABCD的边长为4，E为BC边上一点，BE=3，M为线段AE上的一点，射线BM交正方形的一边于点F，且BF=AE，则BM的长为5/2或12/5。


    正确答案:错误

  • 第21题：

    某工艺条件试验中有六个因子A、B、C、D、E、F，试验人员希望做部分因子试验考察各主效应和AD、AC、BC、DF四个二阶交互效应是否显著，准备采用26-2+4设计，但是MINITAB给出的生成元（Generators）为E=ABC，F=BCD，为了不让可能显著的二阶交互作用相互混杂，下列生成元正确的是：（）

    • A、E=ABD、F=BCD
    • B、E=BCD、F=ABC
    • C、E=ACD、F=BCD
    • D、E=ABD、F=ACD

    正确答案:B

  • 第22题：

    判断题
    若正方形ABCD的边长为4，E为BC边上一点，BE=3，M为线段AE上的一点，射线BM交正方形的一边于点F，且BF=AE，则BM的长为5/2或12/5。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第23题：

    判断题
    已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC，BC为直径作半圆，面积分别记为S1和S2，则S1+S2的值等于4π。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

相关内容