甲、乙、丙各有球若干个,甲给乙的球等于乙现有的那么多球,甲给丙的球等于丙现有的那么多球,然后乙也按甲和丙手中球数分别给甲、丙添球,最后丙也按甲和乙手中的球数分别给甲、乙添球,此时三人各有16个球,问刚开始时甲有多少个球?( )A.26 B.14 C.8 D.10
题目
甲、乙、丙各有球若干个,甲给乙的球等于乙现有的那么多球,甲给丙的球等于丙现有的那么多球,然后乙也按甲和丙手中球数分别给甲、丙添球,最后丙也按甲和乙手中的球数分别给甲、乙添球,此时三人各有16个球,问刚开始时甲有多少个球?( )
A.26 B.14 C.8 D.10
相似考题
更多“甲、乙、丙各有球若干个,甲给乙的球等于乙现有的那么多球,甲给丙的球等于丙现有的那么多球,然后乙也按甲和丙手中球数分别给甲、丙添球,最后丙也按甲和乙手中的球数分别给甲、乙添球,此时三人各有16个球,问刚开始时甲有多少个球?( )A.26 B.14 C.8 D.10”相关问题
-
第1题:
有一个袋子里装有红、白、黑三种颜色的球,共100只。 甲说:“袋子里至少有一种颜色的球少于34只。” 乙说:“袋子里至少有一种颜色的球不少于33只。” 丙说:“袋子里任何两种颜色的球的总和不超过99只。” 以下哪项结论成立?( ) A.甲、乙、丙的看法都正确 B.甲和丙的看法正确,乙的意见不正确 C.乙和丙的看法正确,甲的看法不正确 D.甲和乙的看法正确,丙的看法不正确
正确答案:A
甲的话“袋子里至少有一种颜色的球少于34只”,如果袋子里的三种颜色的球,每一种颜色的球都不少于34只即至少是34只,那么,袋子里的球就不会是100只,而至少是102只了,这当然不行;乙的话“袋子里至少有一种颜色的球不少于33只”,如果袋子里每一种颜色的球都少于33只,那么三种颜色的球的总和至多是99只,这当然不行;丙的话“袋子里任何两种颜色的球的总和不超过99只”,如果袋子里任何两种颜色的球的总和超过99只,即至少是100只,那么,就不会有第三种颜色的球了,这当然不行。所以,甲、乙、丙三个人的看法都是正确的。故选A。
-
第2题:
甲、乙、丙各有球若干,甲给乙的球和乙现有的球一样多,甲给丙的球和丙现有的球一样多,然后乙也按甲和丙手中的球数分别给甲、丙添球,最后丙也按甲、乙手中的球数分别给甲、乙添球,此时三人都各有球16个,开始时甲有多少个球?( )
A.26
B.24
C.32
D.30
正确答案:A
从最后一次开始向前推,第三次,甲有8个,乙有8个,丙有32个,第二次,甲有4个,乙有28个,丙有16个,第一次,甲有26个,乙有14个,丙有8个。 -
第3题:
:有四个外表看起来没有分别的小球,它们的重量可能有所不同。取一个天平,将甲、乙归为一组,丙、丁归为另一组,分别放在天平两边,天平是基本平衡的。将乙、丁对调一下,甲、丁一边明显要比乙、丙一边重得多。可奇怪的是,我们在天平一边放上甲、丙,而另一边则放上乙,还没有来得及放上丁时,天平就压向了乙一边。请你判断,甲球与丁球哪个更重?( )
A.丁球比甲球重
B.丁球比甲球轻
C.甲球与丁球同样重
D.无法确定甲球与丁球的轻重
正确答案:A
根据题意,列出甲、乙、丙、丁四个球重量之间的关系。甲+乙=丙+丁,甲+丁>乙+丙,甲+丙<乙。从这些关系式中可得,甲球比丁球轻,所以选A。 -
第4题:
教师让四名学生每人去拿一只桌球,不论什么颜色。学生拿了球后,教师发现唯一的一只白球被拿走了,问谁拿了白球。甲说:“我没有拿白球。”乙说:“是丁拿的白球。”丙说:“是乙拿的白球。”丁说:“白球不是我拿的。”如果四人中只有一人说的是真话,那么拿了白球的是( )。A.甲
B.乙
C.丙
D.丁答案:A解析:本题为真假推理。乙、丁的话矛盾,必定一真一假,根据“一真其余全假”,可得甲、丙为假。由甲说假话可知拿白球的是甲。 -
第5题:
如图所示,甲、乙两个大小相同的实心金属球放置在光滑水平面上,甲球以水平向右的速度碰撞静止的乙球。已知甲球质量大于乙球,则有关碰撞后的情形。下列说法正确的是( )。 A.甲球可能静止
A.甲球可能静止
B.乙球可能静止
C.甲球可能向左运动
D.甲球一定向右运动答案:D解析:
-
第6题:
甲、乙、丙分别为红、黄、蓝色的三个小球,放在A、B、C三个箱子里。已知①甲球不是蓝色;②黄色球在A中;③B中的球不是红色的;④乙球不在B中,丙球不在A中。下列推断完全正确的是()。A.甲球是红色,在A中
B.甲球是黄色,在C中
C.乙球是黄色,在A中
D.丙球是蓝色,在B中答案:D解析:黄球在A中,B中的球不是红色,则B中球为蓝色,C中球为红色。甲不是蓝色,所以在A或C中,乙球在A或C中。所以,甲在A中、乙在C中,或甲在C中、乙在A中,故丙球在B中。 -
第7题:
现有3个箱子,依次放入1、2、3个球,然后将3个箱子随机编号为甲、乙、丙,接着在甲、乙、丙3个箱子里分别放入其箱内球数的2、3、4倍,共放了22个球。最终甲箱中的球比乙箱()。
- A、多1个
- B、少1个
- C、多2个
- D、少2个
正确答案:A -
第8题:
有甲、乙两个玻璃球,甲球半径的3倍等于乙球半径的2倍,甲球重40克,则乙球重( )克。
- A、140
- B、135
- C、130
- D、125
正确答案:B -
第9题:
在检修机械循环球式转向器、装复螺杆螺母时,甲说“两组钢球应成组交换装入导管螺纹孔”;乙说“两组钢球放在一起挑选分组装入导管螺纹孔”;丙说“两组钢球应分别装入原来的导管螺纹孔”。说法正确的是()。
- A、甲
- B、乙
- C、丙
- D、甲和乙
正确答案:A -
第10题:
判断题甲/乙与丙/丁比赛,甲发球给丁,丙在球着地前触网,然后由于球落在发球区外,判甲发球失误。A对
B错
正确答案: 对解析: 暂无解析 -
第11题:
甲、乙、丙各有球若干个,甲给乙的球如乙现有的那么多球,甲也给丙如丙现有的那么多球,然后乙也按甲和丙手中球数分别给甲、丙添球,最后丙也按甲和乙手中的球数分别给 甲、乙添球,此时三人都各有16个球,问开始时甲有多少个?( ) A.26 B.14 C.8 D.10
正确答案:A
本题属于复杂的还原问题,要求开始时甲的数量,需要从第三次添球开始向前推。第三次添球后,甲、乙、丙三人手中都是16个球,第三次添球之前甲的球数是16÷2=8个;同样,乙的球数是16÷2=8个;第三次添球前丙的球数是16+8+8=32个;第二次添球之后,甲、乙、丙的球数分别是8,8,32。与上面相似,可以求得第二次添球之前甲的球数是8--2=4个;丙的球数是32"2=16个;乙的球数是8+16+4=28个;第一次添球之后,甲、乙、丙的球数分别为4,28,16。第一次添球前乙的球数是28÷2=14个;丙的球数是16-2=8个;甲的球数是4+14+8=26个;所以,开始时,甲、乙、丙三人手中的球数分别为26、14、8。(注意:倒推是解还原问题的主要方法。对于较复杂的还原问题,还常常根据题目特点,将倒推与其他方法结合起来求解。)故选A。
-
第12题:
甲、乙、丙三人手中各有若干颗糖,第一次甲给乙和丙的颗数各等于乙和丙手中原有的颗数,第二次乙给甲和丙的颗数各等于甲和丙两人手中的颗数,第三次丙给甲和乙两人的颗数各等于甲和乙两人手中现有的颗数,这时甲、乙、丙三人手中恰好每人有8颗糖,问丙原有多少颗糖?( )
A.4
B.5
C.6
D.7
正确答案:A
本题用列表法来解,列表,得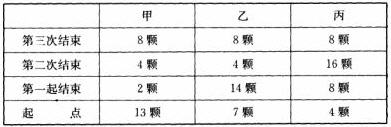
由表可知,第三次丙给甲和乙两人糖后,甲、乙、丙手中各有8颗糖。那么当第二次乙给甲和丙糖后,甲和乙手中各有4颗糖,而丙手中则有16颗糖。同样,第一次结束时,甲、乙、丙三人手中的颗数分别有2颗、14颗和8颗。
依此类推,甲、乙、丙三人原来各有13颗、7颗、4颗糖。本题选A。 -
第13题:
现有3个箱子,依次放人1、2、3个球,然后将3个箱子随机编号为甲、乙、丙,接着在甲、乙、丙3个箱子里分别放人其箱内球数的2、3、4倍。两次共放了22个球,最终甲箱中的球比乙箱()A.多1个
B.少1个
C.多2个
D.少2个答案:A解析:三个箱子臞来一共6个球,所以新放进16个,即2甲+3乙+4丙=16,根据奇数偶数的性质,乙是偶数,所以乙是2个球的箱子,所以甲=3,丙=1,因此甲放了9个球,乙放了8个球,多1个。 -
第14题:
一个暗箱装有12个编号从1到12的乒乓球,甲、乙、丙三人轮流从暗箱中摸球,每人每次摸一个球且不放回。将所有球摸完后,三人所摸出的球上的编号之和相等,并且甲摸出了1号球和3号球,乙摸出了6号球和11号球。丙摸出的球编号最大为多少?A.7
B.8
C.9
D.10答案:C解析:第一步,本题考查其他杂题。
第二步,根据题意可知12个球的数字之和为78,由于每个人摸到四个球且编号之和相等,则每人摸到的编号之和为26;甲摸到1号和3号则剩余两个只能为10和12号;乙摸到6号和11号,则剩余的可能为4号,5号或者为2号,7号;那么9号必为丙摸到的。故丙摸出编号最大的为9号。 -
第15题:
将2个红球与1个白球随机地放入甲、乙、丙三个盒子中,则乙盒中至少有1个红球的概率为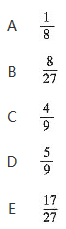 答案:D解析:
答案:D解析: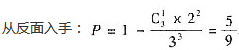
-
第16题:
甲/乙与丙/丁比赛,甲发球给丁,丙在球着地前触网,然后由于球落在发球区外,判甲发球失误。
正确答案:正确 -
第17题:
从某一高度先后由静止释放两个相同的小球甲和乙,若两球被释放的时间间隔为1s,在不计空气阻力的情况下,它们在空中的运动过程中,说法正确的是()
- A、甲、乙两球的距离越来越大,甲、乙两球的速度之差越来越大
- B、甲、乙两球的距离始终保持不变,甲、乙两球的速度之差保持不变
- C、甲、乙两球的距离越来越大,甲、乙两球的速度之差保持不变
- D、甲、乙两球的距离越来越小,甲、乙两球的速度之差越来越小
正确答案:C -
第18题:
关于变速器乱挡的原因。甲认为:变速杆球头限位销松旷.脱落或球头磨损过大是其中之一。乙认为:互锁装置磨损过大或损坏是其中之一。丙认为:变速拔叉磨损过大是其中之一。看法正确的是()。
- A、甲和乙
- B、乙和丙
- C、丙和甲
- D、均错
正确答案:A -
第19题:
单选题现有3个箱子,依次放入1、2、3个球,然后将3个箱子随机编号为甲、乙、丙,接着在甲、乙、丙3个箱子里分别放入其箱内球数的2、3、4倍,共放了22个球。最终甲箱中的球比乙箱()。A多1个
B少1个
C多2个
D少2个
正确答案: B解析: 由题知,甲、乙、丙3个箱子里最终的球数为原球数的3、4、5倍,而原来的球数是1或2或3,设三个箱子原来分别有x、y、z个球,则有x+y+x=6……(1),3x+4y+5x=22……(2),因为比较的是甲和乙的关系,因此我们将z消去,用5×(1)-(2)得2x+y=8.如果x=1,y=6,不符合,如果x=2,y=4,不符合,于是x=3,y=2,选A。
