有20名工人修筑一段公路，计划15天完成。动工3天后抽出5人去其他工地，其余人继续修路。如果没人工作效率不变，那么修完这段公路实际用（）A.19天 B. 18天 C. 17天 D. 16天

题目

有20名工人修筑一段公路，计划15天完成。动工3天后抽出5人去其他工地，其余人继续修路。如果没人工作效率不变，那么修完这段公路实际用（）

A.19天   B. 18天   C. 17天   D. 16天

相似考题

1.某筑路队承担了修一条公路的任务。原计划每天修720米，实际每天比原计划多修80米，这样实际修的差1200米就能提前3天完成。这条公路全长多少米?

2.7，14，10，11，14，9，（ ），8 A．19 B．18 C．17 D．16

3.一项工程，甲单独完成需要2天，乙单独完成需要4天，如果甲干完一天后，剩下的工程由乙单独完成，则于完此项工程共需要（ ）天。A．3B．4C．5D．6

4.某玩具厂收到一份订单，按计划8天可完成任务的2/5，如果生产了3天后，将工作效率提高了1/8，又继续工作4天，一共完成了这份订单的( )。A．3/8B．59/160C．5/8D．3/16

更多“有20名工人修筑一段公路，计划15天完成。动工3天后抽出5人去其他工地，其余人继续修路。如果没人工作效率不变，那么修完这段公路实际用（）A.19天B.18天C.17天D.16天”相关问题

  • 第1题：

    在复习一般应用题时，教师出示一道题：某修路队修一天公路，计划每天修60天，7天修完。若需提前1天修完，平均每天比计划多修几米? 甲解：60×7÷(7-1)-60=420÷6-60=70-60=10(米) 乙解：60÷(7-1)=60÷6=10(米)，她说：这条公路计划7天修完，若提前1天修完，只能用6天。在6天里平均每天比计划多修的米数加起来等于计划1天修的米数加起来等于计划1天修的米数，所以只要把60除以6即可。大家对乙另辟蹊径的最简解法十分赞赏，但是又说不清为什么要这样解。这时，丙提出质疑，他说：用乙的算法，若需提前6天只能修完，60÷(7-6)=60米，60+60=120(米)，即1天只能修120米，而公路全程有420米，是不可能提前6天修完的。教师表扬丙敢于质疑，并启发说：我们画个图，结合图形来研究好吗?于是师生共同作图如下：

    在(1)中，提前1天用6天修完，只要1天的工作量分成6份，平均分配到6天的工作时间中去，就是说若要提前1天修完，每天就要比原来多修“60÷6=10”米。乙的解法实际上是60×7÷(7-1)，这里把“×1”省略了是可以的。 在(2)中，提前6天用1天修完，那么就要把6天的工作量60×6=360(米)都加到1天的工作量中去，即60×6+60=420(米)。 最后，引导学生反思和评价这一段学习过程，有这样几点看法：(1)两种解法都是正确的，甲是一般解法，乙的解法更为简便。(2)同学们在解题过程中有说不清楚，或者有怀疑的地方要敢于提问，提得出问题是进步的开始。(3)根据题意作出草图，可以帮助我们理清思路。


    正确答案：本例通过一题多解培养发散思维。所谓发散思维，是指多角度、多方向、多层次的一种思维方式。创新是对旧的突破。没有发散思维，墨守成规，就谈不上创新。通过发散思维获得多种解法之后，还要运用聚合思维，通过比较，选取最优解。在本例中，学生赞赏了乙的最简解法，丙未真正理解，持怀疑态度，言语中有反唇相讥之味。我若以此加以否定或让他当众出丑，那对丙的学习激情和批判冲动将是一种残酷打击。实质上乙的解法只是“提前1天”的特例，而丙要寻求的却是“提前n天”的通解，这也是丙的思维中创新的火花。我在鼓励的同时启发他们用线段图辅助思考，列出算式，这样丙可以理直气壮地说出解题思路，获得认知与情感上的满足。在创新教育中，老师的宽容态度很重要，没有宽容心，就没有学生的自信心，没有自信心也就会失去创造的内驱力，无法培养学生的批判思维和创新精神。

  • 第2题：

    有20名工人修筑一段公路，计划l5天完成。动工3天后抽出5人去其他工地，其余人继续修路。如果每人工作效率不变，那么修完这段公路实际用（ ）。

    A．19天

    B．18天

    C．17天

    D．16天


    正确答案：A

  • 第3题：

    一条公路，甲、乙两队合修8天可完，乙、丙两队合修6天可完，丙、丁两队合修12天可完，那么甲、丁两队合修多少天可完?( )

    A．15

    B．18

    C．20

    D．24


    正确答案：D

  • 第4题：

    甲、乙两个工程队修路，最终按工作量分配8400元工资。按两队原计划的工作效率，乙队应获5040元。实际从第5天开始，甲队的工作效率提高了1倍，这样甲队最终可比原计划多获得960元。那么两队原计划完成修路任务要多少天？( )

    A．12

    B．15

    C．18

    D．9


    正确答案：A
    A【解析】开始时甲队拿到8400-5040=3360元，甲、乙的工资比等于甲、乙的工作量的比，即为3360/5040；甲提高工效后，甲、乙的工资及工作量的比为(3360+960)/(5040-960)=18/17;设甲开始的工效为“2"，那么乙的工效为“3”，设甲在提高工效后还需x天完成任务。有(2×4+4x)/(3×4+3x)=18/17，化简为216+54x=136+68x，解得x=40/7等。于是共有工程量为4×5+7×40/7=60，所以原计划60÷(2+3)=12天完成。故答案为A。

  • 第5题：

    单独完成一项工作，甲按规定时间可提前3天完成，乙则要超过规定时间5天才能完
    成。如果甲、乙合作3天后剩下的工作继续由乙单独做，那么刚好在规定时间里完成。甲、乙两人合作要几天完成?

    A.7
    B.8
    C.7．5
    D.6

    答案：C
    解析：
    显然甲3天的工作量相当于乙5天的工作量。因此甲完成的天数：乙完成的天数=3：5。设甲完成工作需3x天，则乙需5x天，5x一3x=8，解之得x＝4，因此甲独立完成需要3x4=12天，乙需要5x4=20天。二

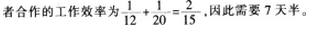
  • 第6题：

    有20名工人修筑一段公路，计划15天完成。动工3天后抽出5人去其他工地，其余人 继续修路。如果每人工作效率不变，那么修完这段公路实际用( ).

    A.19天
    B.18天
    C.117天
    D.16天

    答案：A
    解析：
    5人12天完成的工作量分配给15人需要5x12÷15=4天完成，所以修完这段公路实际用 15+4=19 天。

  • 第7题：

    有20名工人修筑一段公路，计划15天完成。动工3天后抽出5人去其他工地，其余人继续修路。如果每人工作效率不变，那么修完这段公路实际用（）。

    A.19 天
    B.18 天
    C.17 天
    D.16 天

    答案：A
    解析：
    5人12天完成的工作量分配给15人需要5×12÷15=4天完成,所以修完这段公路实际用 15+4=19 天。

  • 第8题：

    有20名工人修筑一段公路，计划15天完成。动工3天后抽出5人去其他工地，其余人继续修路。如果每人工作效率相同且不变，那么修完这段公路实际用：
    A 19天
    B 18天
    C 17天
    D 16天


    答案：A
    解析：

  • 第9题：

    甲、乙、丙三人合修一条公路，甲、乙合修6天修好公路的1/3 ，乙、丙合修2天修好余下的1/4 ，剩余的三人又修了5天才完成。共得收入1800元，如果按工作量计酬，则乙可获得收入为（ ）

    A. 330元
    B. 910元
    C. 560元
    D. 980元

    答案：B
    解析：
    设甲、乙、丙三人的工作效率分别为 x、y 、z ，可列三元一次方程为 6*((x+6)=1/3，2*(x+y)=(1-1/3)*(1/4) ，5*(x+y+z)=1-1/3-(1-1/3)*1/4 ，解x=1/60 ，y=1/180 ，z=1/22.5 。乙一共工作了 天，完成全部工作量的 ，应得910元。故答案为B。

  • 第10题：

    某仓库内有一批货物，如果用3辆大卡车，4天可以运完；如果用4辆小卡车，5天可以运完；如果用20辆板车，6天可以运完。现在先用2辆大卡车、3辆小卡车和7辆板车共同运2天后，全部改用板车运，必须在两天内运完，那么后两天每天至少需要多少辆板车?

    A.12
    B.15
    C.16
    D.18

    答案：B
    解析：

  • 第11题：

    某工程队预计30天修完一条水渠，20人修了12天后完成工程的一半，如果要提前10天完成，还要增加（）人。

    • A、7人
    • B、8人
    • C、9人
    • D、10人

    正确答案:D

  • 第12题：

    单选题
    建筑公司安排100名工人去修某条路，工作2天后抽调走30名工人，又工作了5天后再抽调走20名工人，总共用时12天修完。如希望整条路在10天内修完，且中途不得增减人手，则要安排多少名工人？（）
    A

    80

    B

    90

    C

    100

    D

    120


    正确答案： D
    解析： 假设每个工人每天工作量为1，则这条路的工作量为100×2+（100-30）×5+（100-30-20）×5=800，如果要在10天内修完，则要安排800÷10=80名工人。

  • 第13题：

    甲、乙两个工程队同时抢修一段距离相等的公路，开工12天后，两队完成的工作量正好等于甲队的总工作量。开工20天后，乙完成了任务，甲队还需再修300米才完成任务。两段公路的总长度是多少米？

    A.2400B.2000C.1800D.1500


    乙用20天完成任务，那么12天时完成了5分之3，因为12天时甲乙刚好完成了甲的工作量，那么甲在12天时就完成了5分之2，
    甲要完成任务的时间就是：12/（1－12/20）＝30
    这样我们就知道甲前20天完成了30分之20的任务，剩下的300米相当于30分之10的工作量，这样就可算出甲修的路的长度为：300/（1－20/30）＝900米。这两段公路的总长度就是：900*2＝1800米

    乙用20天完成任务，那么12天时完成了5分之3，因为12天时甲乙刚好完成了甲的工作量，那么甲在12天时就完成了5分之2，
    甲要完成任务的时间就是：12/（1－12/20）＝30
    这样我们就知道甲前20天完成了30分之20的任务，剩下的300米相当于30分之10的工作量，这样就可算出甲修的路的长度为：300/（1－20/30）＝900米。这两段公路的总长度就是：900*2＝1800米

  • 第14题：

    有20人修筑一条公路，计划l5天完成。动工3天后抽出5人植树，留下的人继续修路。如果每人工作效率不变，那么修完这段公路实际要用多少天?( )

    A．16

    B．17

    C．18

    D．19


    正确答案：D

  • 第15题：

    修一段公路，甲队单独做要40天完成，乙队单独做需要24天，现在两队从两端同时开工，最后在距中点750米处相遇。那么这段公路长多少米?

    A．3000

    B．4000

    C．4500

    D．6000


    正确答案：D
    [答案] D[解析]甲队和乙队的效率比为24:40=3:5，因此同样时间的工作量之比也为3:5，而乙队比甲队多修了750×2=1500米，因此公路全长为1500÷(5-3)×(5+3)=6000米。

  • 第16题：

    甲乙两个工程队承担了精准扶贫村公路的修筑任务，先是甲工程队单独修了10天，完成了总工程的四分之一，接着乙工程队加入合作，完成剩余工程。在第14天完成到总工程的一半，则按照这种进度完成全部工程所用的天数比由甲单独完成这项工程少用的天数是

    A.12天
    B.20天
    C.18天
    D.16天

    答案：C
    解析：
    第一步，本题考查工程问题，要熟悉工程量、工作时间和工作效率三者之间的比例关系。第二步，甲完成四分之一需要10天，则完成全部工程需要40天；甲乙合作后在第14天完成一半，即甲和乙合作4天完成四分之一，剩下的一半甲和乙合作需要8天，即一共需要14＋8＝22天完成，则比甲单独完成这项工程少用的天数为18天。因此，选择C选项。

  • 第17题：

    建筑公司安排100名工人去修某条路，工作2天后抽调30名工人，又工作了 5天后再抽走20名工人，总共用时12天修完。如果整条路希望在10天内修完，且中途不得增减人手，则要安排多少名工人？（）

    A.80名
    B.90名
    C.100名
    D.120名

    答案：A
    解析：
    设每个人工作效率为1,则工作总量=100×2+70×5+50×(12—2—5)=800,10天完成效率应为80,即80个人。故选A。

  • 第18题：

    有一条公路，甲队独修需10天，乙队独修需12天，丙队独修需15天，修完第一条公路后，三队又去维修两条规模更大的公路A和B，且修这两条公路所需的工作量相同，甲修A公路，乙修B公路，丙先帮甲后帮乙，结果用了16天才修完这两条公路，问丙在A公路修了多少天？（ ）

    A. 6
    B. 7
    C. 8
    D. 9

    答案：A
    解析：

  • 第19题：

    有20名工人修筑一段公路，计划15天完成。动工3天后抽出5人去其他工地，其余人继续修路。如果没人工作效率不变，那么修完这段公路实际用（）


    A. 19天
    B. 18天
    C. 17天
    D. 16天

    答案：A
    解析：
    解题指导： 设总工程为20*15，设一人一天做1个单位，动工了3天后已经做了20*3*1=60，还剩240个单位，现在是来求15人要多长时间来完成240个单位。有15*1*t=240.t=16天，最后完成所有工程用了19天。故答案为A。

  • 第20题：

    某行政村计划15天完成春播任务1500亩，播种5天后，由于更新机械，工作效率提高25％，问这个行政村会提前几天完成这1500亩的春播计划?（　　）
    A.4天
    B.3天
    C.2天
    D.1天


    答案：C
    解析：
    根据题意可知，剩余的春播任务为15—5=10天，因工作效率提高25％，则完成剩余的春播任务为10÷(1+25%)=8天，因此整个行政村会提前10一8=2天完成1500亩的春播任务。

  • 第21题：

    某工程由10名工人承担，5天后，为了要提前10天完成任务，需增加4名工人，那按计划完成该工程需要（　　）天。(假设所有工人的工作效率相同)

    A.35
    B.40
    C.65
    D.80

    答案：B
    解析：

    10-5。解得a=40，选B。

  • 第22题：

    有20人修筑一条公路，计划15天完成。动工3天后抽出5人植树，留下的人继续修路。如果每人工作效率不变，那么修完这段公路实际用多少天？

    A. 16
    B. 17
    C. 18
    D. 19

    答案：D
    解析：
    20人每天修1/15所以一个人每天修1/3003天修了全部的1/5，所以剩下的4/5需要4/5÷15/300=16天实际用了16+3=19天

  • 第23题：

    单选题
    某仓库内有一批货物，如果用3辆大卡车，4天可以运完；如果用4辆小卡车，5天可以运完；如果用20辆板车，6天可以运完。现在先用2辆大卡车、3辆小卡车和7辆板车共同运2天后，全部改用板车运，必须在两天内运完，那么后两天每天至少需要多少辆板车？
    A

    12

    B

    15

    C

    16

    D

    18


    正确答案： B
    解析： 暂无解析

相关内容