某单位围墙外面的公路围成了边长为300米的正方形,甲乙两人分别从两个对角沿逆时针同时出发,如果甲每分钟走90米,乙每分钟走70米,那么经过( )甲才能看到乙A.16分40秒 B.16分 C.15分 D.14分40秒
题目
某单位围墙外面的公路围成了边长为300米的正方形,甲乙两人分别从两个对角沿逆时针同时出发,如果甲每分钟走90米,乙每分钟走70米,那么经过( )甲才能看到乙
A.16分40秒 B.16分 C.15分 D.14分40秒
相似考题
更多“某单位围墙外面的公路围成了边长为300米的正方形,甲乙两人分别从两个对角沿逆时针同时出发,如果甲每分 ”相关问题
-
第1题:
甲、乙两人在长30米的泳池内游泳,甲每分钟游37.5米,乙每分钟游52.5米,两人同时分别从泳池的两端出发,触壁后原路返回,如是往返。如果不计转向的时间,则从出发开始计算的1分50秒内两人共相遇了多少次?
A.2
B.3
C.4
D.5
正确答案:B
【解析】B。本题属于行程问题。泳池长30米,两人速度和为90米/分,则两人相遇时所走的路程和应为1×30,3×30,5×30,7×30……,而1分50秒两人游了90×11/6=165米,所以最多可以相遇3次,所以选择B选项。 -
第2题:
某单位围墙外面的公路围成了边长为300米的正方形,甲乙两人分别从两个对角沿逆时针同时出发,如果甲每分钟走90米,乙每分钟走70米,那么经过多少时间甲才能看到乙?( )
A. 16分40秒
B. 16分
C. 15分
D. 14分40秒答案:A解析:解题指导: 由题意可得:甲乙之间相距600米,甲乙的速度差为20米/分,当甲乙相差300米,所用时间为15分钟,此时甲共走1350米(四条边余150米),乙共走1050米(3条边余150米),两个人此时处于不同的边上。甲还需走150米才能到达乙在的那条边上,即需100秒,而100秒后,乙走了700/6米,700/6+150<300,所以此时两人正好处在同一条边,故答案为A。 -
第3题:
甲、乙两人在长30米的泳池内游泳,甲每分钟游37. 5米,乙每分钟游52. 5米。两人同时分别从泳池的两端出发,触壁后原路返回,如是往返。如果不计转向的时间,则从出发开始计算的1分50秒内两人共相遇了多少次?( )
A. 2 B. 3 C. 4 D. 5答案:B解析:分析题意,甲乙第一次相遇时两人共游了30米,此后两人每共游一个来回即60米时再次相遇。1分50秒内两人共游了(37.5 + 52.5)X11/6= 165(米),故应相遇了 3次,分别在30米、90米和150米时,答案选B。 -
第4题:
一个正六边形跑道,每边长为100米。甲乙两人分别从两个相对的顶点同时出发,沿跑道相向匀速前进。第一次相遇时甲比乙多跑了60米,问甲跑完三圈时,两人之间的直线距离是多少?
A.100米
B.150米
C.200米
D.300米
正确答案:C
正六边形跑道,甲、乙两人从两个相对的顶点沿跑道相向出发。第一次相遇时,甲、乙两人走过的路程和为100×3=300米。且甲比乙多跑了60米,可以得到甲走过的路程为(300+60)÷2=180米,乙走过的路程为300-180=120米。
相同时间内。两人的速度比等于180:120=3:2,所以当甲跑完三周时,乙跑完了两圈,
两人同时回到原出发点。此时,两人之间的距离如图所示,为正六边形的对角线。
由下图可以看出.正六边形的对角线等于边长的2倍,故直线距离为100×2=200米。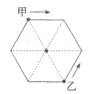
-
第5题:
一个正方形跑道边长为20米,甲和乙从跑道上的不同位置同时出发,匀速沿逆时针跑步,已知两人出发的位置之间直线距离为20米,甲以2米/秒的速度跑6秒到达某个顶点后,又跑了不到10秒正好到达乙出发的位置,此时乙正好第二次跑到顶点位置。问以下哪个描述是正确的?( )A.甲出发后不到2分钟第一次追上乙
B.甲出发后超过2分钟第一次追上乙
C.乙出发后不到2分钟第一次追上甲
D.乙出发后超过2分钟第一次追上甲答案:A解析:本题属于行程问题。
由甲以2米/秒的速度跑6秒到达某个顶点,画出图示。如图所示: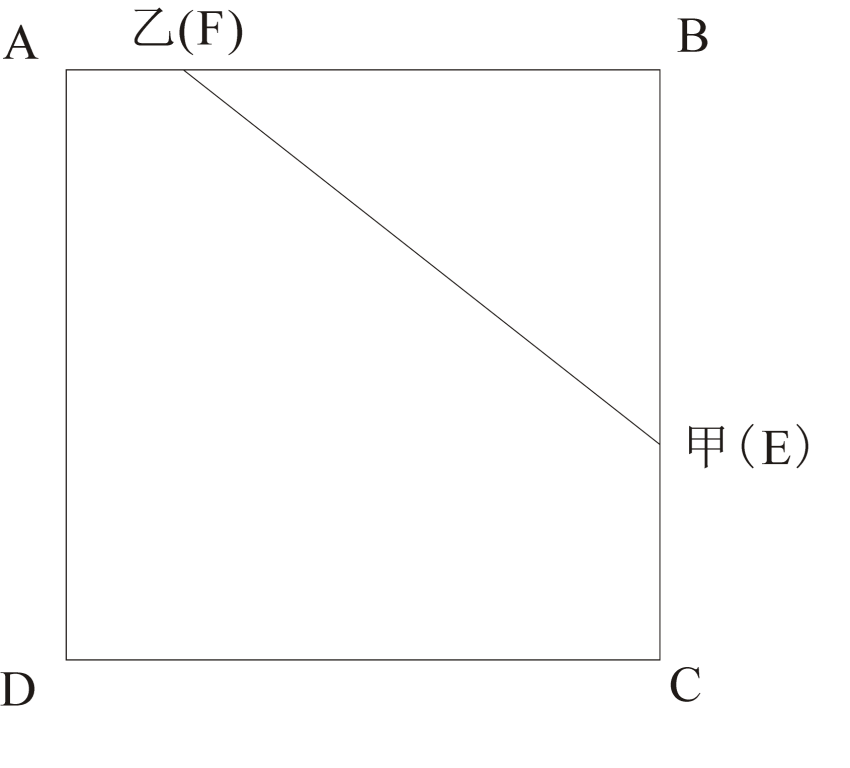
甲初始位置在E点,EB=6×2=12米,由题意又跑了不到10秒正好到达乙出发的位置,所以画出示意图乙出发点在F点,且EF=20。由勾股定理可求得BF=16。甲到达乙的出发点共用时(12+16)÷2=14秒。又因为此时乙正好第二次跑到顶点位置,即跑到了D点,所以乙的速度为(4+20)÷14=12/7。甲的速度大于乙的速度,所以甲出发后,追上乙需要的时间为(12+16)÷(2-12/7)=98s。A符合题意。
因此,选择A选项。
