一个圆桌围了6个孩子每个人想一个数,告诉旁边人,求平均数6个人围成一圈每个人心里想一个数,并把这个数告诉左右相邻的两个人,每个人把左右相邻的人告诉自己的数的平均数亮出来,两处数为22的人心里想多少
题目
6个人围成一圈每个人心里想一个数,并把这个数告诉左右相邻的两个人,每个人把左右相邻的人告诉自己的数的平均数亮出来,两处数为22的人心里想多少
相似考题
更多“一个圆桌围了6个孩子每个人想一个数,告诉旁边人,求平均数 6个人围成一圈每个人心里想一个数,并把这个数告诉左右相邻的两个人,每个人把左右相邻的人告诉自己的数的平均数亮出来,两处数为22的人心里想多少”相关问题
-
第1题:
五个数中,最小的是12,从第一个数起,每一个数都比前一个数大5,这五个数的平均数是多少?( )
A.22
B.22.5
C.23
D.23.5
正确答案:A
五个数构成等差数列,所以五个数的平均数是中间数,即第三个数为12+5+5=22。正确答案为A。 -
第2题:
第五题. 推理游戏
教授选出两个从2到9的数,把它们的和告诉学生甲,把它们的积告诉学生乙,让他们轮流猜这两个数
甲说:“我猜不出”
乙说:“我猜不出”
甲说:“我猜到了”
乙说:“我也猜到了”
问这两个数是多少
正确答案:第五题:3和4(可严格证明)
设两个数为n1,n2,n1>=n2,甲听到的数为n=n1+n2,乙听到的数为m=n1*n2
证明n1=3,n2=4是唯一解
证明:要证以上命题为真,不妨先证n=7
1)必要性:
i) n>5 是显然的,因为n<4不可能,n=4或者n=5甲都不可能回答不知道
ii) n>6 因为如果n=6的话,那么甲虽然不知道(不确定2+4还是3+3)但是无论是2,4还是3,3乙都不可能说不知道(m=8或者m=9的话乙说不知道是没有道理的)
iii) n<8 因为如果n>=8的话,就可以将n分解成 n=4+x 和 n=6+(x-2),那么m可以是4x也可以是6(x-2)而4x=6(x-2)的必要条件是x=6即n=10,那样n又可以分解成8+2,所以总之当n>=8时,n至少可以分解成两种不同的合数之和,这样乙说不知道的时候,甲就没有理由马上说知道。
以上证明了必要性
2)充分性
当n=7时,n可以分解成2+5或3+4
显然2+5不符合题
第五题:3和4(可严格证明)
设两个数为n1,n2,n1>=n2,甲听到的数为n=n1+n2,乙听到的数为m=n1*n2
证明n1=3,n2=4是唯一解
证明:要证以上命题为真,不妨先证n=7
1)必要性:
i) n>5 是显然的,因为n<4不可能,n=4或者n=5甲都不可能回答不知道
ii) n>6 因为如果n=6的话,那么甲虽然不知道(不确定2+4还是3+3)但是无论是2,4还是3,3乙都不可能说不知道(m=8或者m=9的话乙说不知道是没有道理的)
iii) n<8 因为如果n>=8的话,就可以将n分解成 n=4+x 和 n=6+(x-2),那么m可以是4x也可以是6(x-2)而4x=6(x-2)的必要条件是x=6即n=10,那样n又可以分解成8+2,所以总之当n>=8时,n至少可以分解成两种不同的合数之和,这样乙说不知道的时候,甲就没有理由马上说知道。
以上证明了必要性
2)充分性
当n=7时,n可以分解成2+5或3+4
显然2+5不符合题意,舍去,容易判断出3+4符合题意,m=12,证毕
于是得到n=7 m=12 n1=3 n2=4是唯一解。
意,舍去,容易判断出3+4符合题意,m=12,证毕
于是得到n=7 m=12 n1=3 n2=4是唯一解。
-
第3题:
有4个数,每次选出3个算他们的平均数,再加上另一个数,用这种方法计算了4次,分别得到4个数:86、92、100和106,那原来这4个数的平均数是()
A.48
B.42
C.36
D.32
正确答案:A
-
第4题:
十个人围成一个圆圈,每人选择一个整数并告诉他的两个邻座的人,然后每人算出并宣布他两个邻座所选数的平均数,这些平均数如右图所示,则宣布6的那个人选择的数是多少?
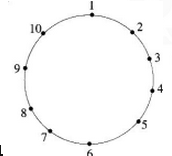 A.l
A.l
B.2
C.3
D.4答案:B解析:设宣布1~10的人选择的数分别是,a1,a2,a3,,…am。由图形可知a2+a4=3×2=6,a4+a6=5×2=10,a6+a8=7×2=14,a6+a8=9×2=18,a10+a2=1×2=2,等式左右分别相加,得到2(a2+a4+a6+a8+a10)=6+10+14+18+2=50,则(a2+a4)+a4+(a8+a10)=25,所以a6=25-6-18=1,应选择A。 -
第5题:
有a、6、c三个数,首先加入27这个数,此时这四个数的平均数是36;然后撤出数c,余下三个数的平均数是37;然后撤出27,余下两个数之差是24,问a、b、c三个数中第二大的数是多少?( )A.33
B.48
C.54
D.60答案:A解析:由题意可知a+b+c+27=36x4,a+b+27=37x3,由此可知c=33,a+b=84。又a,b之差为24,所以a,b中较大的数是(84+24)÷2=54,较小的数是(84-24)÷2=30,所以a,b,c中第二大的数是c=33。 -
第6题:
有5个数的算术平均数为17,去掉其中一个数后,算术平均数为21,试问去掉的那个数是多少?( )A. 4
B. 3
C. 2
D. 1答案:D解析:17×5-21×4=1,故答案为D。 -
第7题:
给定一组数据X,关于X的平均数、中位数、众数,下列说法正确的是()。
- A、平均数一定是这组数中的某个数
- B、中位数一定是这组数中的某个数
- C、众数一定是这组数中的某个数
正确答案:C -
第8题:
单选题有四个数,去掉最大的数,其余三个数的平均数是41,去掉最小的数,其余三个数的平均数是60,最大数与最小数的和是95。则这四个数的平均数是( )。A49.75
B51.25
C53.75
D54.75
正确答案: D解析:
将三种情况合在一起看做整体,则每个数字恰好被计算两次,因此这四个数的平均数是(41×3+60×3+95)÷2÷4=49.75。 -
第9题:
五个数中,最小的是12,从第二个数起,每一个数都比前一个数大5,这五个数的平均数是( )。
A.22
B.22.5
C.23
D.23.5
正确答案:A
由题意可知,这5个数分别为12、17、22、27、32,易知其平均数为22。 -
第10题:
有5个数的算术平均数为25,去掉其中一个数后,算术平均数为31,试问去掉的那个数是多少?( )
A.4
B.3
C.1
D.2
正确答案:C
-
第11题:
一串数字共15个,前10个的平均数是23,后10个的平均数是35,中间5个的平均数是26,这15个数字的平均数是多少?
A.33
B.31.5
C.30
D.29
正确答案:
前10个数之和为23×10=230,后10个数之和为35×10=350,中间5个数之和为26×5= 130。将前10个数和后10个数相加,则中间5个数算了两次,因此15个数之和为230+350-130=450,平均数为450÷15=30。
-
第12题:
有一列数,第一个数为8,第二个数为4,从第二个数起,它们的每个数都比它前后相邻的两数的和少5,从第一个数到第2003个数的和是( )。
A.10001 B.10000 C.10011 D.11000答案:C解析:
-
第13题:
有a、b、c三个数,首先加人27这个数,此时这四个数的平均数是36;然后撤出数c,余 下三个数的平均数是37;然后撤出27,余下两个数之差是24,问a、b、c三个数中第二大的数是 多少?
A.33
B.48
C.54
D.60答案:A解析:由题意可知a+6+c+27=36x4,a+6+27=37x3,由此可知c=33,a+6=84。又a,b之差为24, 所以a’b中较大的数是(84+24)÷2=54,较小的数是(84-24)÷2=30,所以a’b’c中第二大的数是a=33。 -
第14题:
A、B、C、D四个数,每次去掉一个数,将其余三个数求平均数,这样计算了4次,得到23,26,30,33四个数,则A、B、C、D四个数的平均数是()。
- A、27
- B、28
- C、29
- D、30
正确答案:B -
第15题:
对于不同水平的数列,通过标准差指标,()。
- A、可以直接比较两个数列的平均数的相对差异
- B、可以直接比较两个数列的平均数的绝对差异
- C、可以直接比较两个数列的平均数的代表性大小
- D、不能直接比较两个数列的平均数的代表性大小
正确答案:D -
第16题:
单选题对于不同水平的数列,通过标准差指标,()。A可以直接比较两个数列的平均数的相对差异
B可以直接比较两个数列的平均数的绝对差异
C可以直接比较两个数列的平均数的代表性大小
D不能直接比较两个数列的平均数的代表性大小
正确答案: A解析: 暂无解析
