设 A 为方阵, f（x), g（x)为多项式, B = f（A), C = g（A), 则BC = CB.

题目

相似考题

1.设函数f(x)=lnx，g(x)=e2x+1，则f[g(x)]=______。

2.设f(x),g(x),h(x)均为奇函数,则()中所给定的函数是偶函数。A、f(x)g(x)h(x)B、[f(x)+g(x)]h(x)C、f(x)+g(x)D、f(x)+g(x)+h(x)

3.设f (x)=x2,g(x)=ex,则f [g(x)]=_________.

4.设f(x)=3x,g(x)=x2，则函数g[f(x)]-f[g(x)]=_______________.

参考答案和解析

更多“设 A 为方阵, f（x), g（x)为多项式, B = f（A), C = g（A), 则BC = CB.”相关问题

第1题：

设函数f(x)为奇函数,g(x)为偶函数,则复合函数()是奇函数。

A.f(f(x))
B.g(f(x))
C.f(g(x))
D.g(g(x))

正确答案：A
第2题：

设f（x）为偶函数，g（x）为奇函数，则下列函数中为奇函数的是（　　）。

A． f[g（x）]
B． f[f（x）]
C． g[f（x）]
D． g[g（x）]

答案：D
解析：
D项，令T（x）＝g[g（x）]。因为T（－x）＝g[g（－x）]＝g[－g（x）]＝－g[g（x）]，所以T（－x）＝－T（x），所以g[g（x）]为奇函数。
第3题：

设函数f（x），g（x）是大于零的可导函数，且f′（x）g（x）-f（x）g′（x）＜0，则当a＜x＜b时有（）《》（）

A.f（x）g（b）＞f（b）g（x）
B.f（x）g（a）＞f（a）g（x）
C.f（x）g（x）＞f（b）g（b）
D.f（x）g（x）＞f（a）g（a）

答案：A
解析：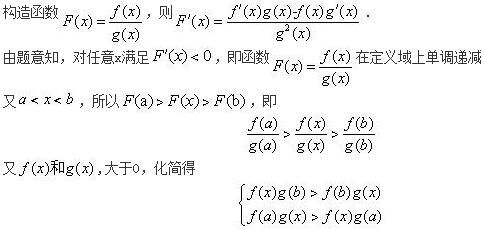
第4题：

对于任意f（x）∈F[x]，f（x）都可以整除哪个多项式？（）
- A、f（x+c）c为任意常数
- B、0.0
- C、任意g（x）∈F{x]
- D、不存在这个多项式
正确答案:B
第5题：

若f（x）与g（x）互素，则f（x）与g（x）的公因式都是零多项式。

正确答案:错误
第6题：

设单调可微函数f(x)的反函数为g(x),f(1)=3,f′(1)=2,f″(3)=6则g′(3)=（）

正确答案:1/2
第7题：

设K是个数域，K[x]中的多项式f（x），g（x），若有f=g，则可以得到什么？（）
- A、f（x）=g（f（x））
- B、g（x）=f（f（x））
- C、f（x）=g（x）
- D、g（x）=f（g（x））
正确答案:C
第8题：

单选题
设f（x）为偶函数，g（x）为奇函数，则下列函数中为奇函数的是（）。
A
f[g(x)]
B
f[f(x)]
C
g[f(x)]
D
g[g(x)]

正确答案： D
解析：
第9题：

填空题
设单调可微函数f(x)的反函数为g(x),f(1)=3,f′(1)=2,f″(3)=6则g′(3)=（）

正确答案： 1/2
解析：暂无解析
第10题：

单选题
设K是个数域，K[x]中的多项式f（x），g（x），若有f=g，则可以得到什么？（）
A
f（x）=g（f（x））
B
g（x）=f（f（x））
C
f（x）=g（x）
D
g（x）=f（g（x））

正确答案： C
解析：暂无解析
第11题：

判断题
在数域K中多项式f（x）与g（x）若有f=g，则f（x）=g（x）。
A
对
B
错

正确答案：对
解析：暂无解析
第12题：

单选题
对于任意f（x）∈F[x]，f（x）都可以整除哪个多项式？（）
A
f（x+c）c为任意常数
B
0.0
C
任意g（x）∈F{x]
D
不存在这个多项式

正确答案： A
解析：暂无解析
第13题：

设f(x)，g(x)ϵP[x J. 若f(x)lg(x)，g(x)lf(x)，则 f(x)与g(x)的关系是( ).

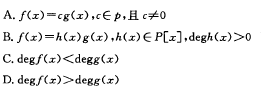参考答案：A
第14题：

设函数f（x），g（x）在[a，b]上均可导（a＜b），且恒正，若f′（x）g（x）＋f（x）g′（x）＞0，则当x∈（a，b）时，下列不等式中成立的是（　　）。

A． [f（x）/g（x）]＞[f（a）/g（b）]
B． [f（x）/g（x）]＞[f（b）/g（b）]
C． f（x）g（x）＞f（a）g（a）
D． f（x）g（x）＞f（b）g（b）

答案：C
解析：
因为[f（x）g（x）]′＝f′（x）g（x）＋f（x）g′（x）＞0，所以函数f（x）g（x）在[a，b]上单调递增。所以，当x∈（a，b）时，f（a）g（a）＜f（x）g（x）＜f（b）g（b）。
第15题：

在F（x）中，f（x），g（x）是次数≤n的多项式，若在F中有n+1个不同的元素，c1，c2…使得f（ci）=g（ci），则f（x）=g（x）。

正确答案:正确
第16题：

互素多项式的性质，若f（x）|g（x）h（x），且（f（x），g（x））=1，那么可以推出什么？（）
- A、g（x）
- B、h（x）
- C、f（x）g（x）
- D、f（x）
正确答案:D
第17题：

若f′（x）=g′（x），则下列哪个式子成立（）？
- A、f（x）=g（x）
- B、f（x）>g（x）
- C、f（x）
- D、f（x）=g（x）+cc为任意常数
正确答案:D
第18题：

设F（x），G（x）是f（x）的两个原函数，则下面的结论不正确的是（）。
- A、F（x）+C也是f（x）的原函数，C为任意常数
- B、F（x）=G（x）+C，C为任意常数
- C、F（x）=G（x）+C，C为某个常数
- D、F’（x）=G’（x）
正确答案:B
第19题：

在数域K中多项式f（x）与g（x）若有f=g，则f（x）=g（x）。

正确答案:正确
第20题：

判断题
若f（x）与g（x）互素，则f（x）与g（x）的公因式都是零多项式。
A
对
B
错

正确答案：对
解析：暂无解析
第21题：

判断题
在F（x）中，f（x），g（x）是次数≢n的多项式，若在F中有n+1个不同的元素，c1，c2…使得f（ci）=g（ci），则f（x）=g（x）。
A
对
B
错

正确答案：错
解析：暂无解析
第22题：

问答题
设函数f（x），g（x）二次可导，满足函数方程f（x）g（x）＝1，又f′（x）≠0，g′（x）≠0，则f″（x）/f′（x）－f′（x）/f（x）＝g″（x）/g′（x）－g′（x）/g（x）。

正确答案：
f(x)g(x)=1,则f′(x)g(x)+f(x)g′(x)=0①
即f′(x)/f(x)=-g′(x)/g(x)②
对①两边求导得f″(x)g(x)+2f′(x)g′(x)+f(x)g″(x)=0,即f″(x)+2f′(x)g′(x)/g(x)+f(x)g″(x)/g(x)=0,即f″(x)/f′(x)+2f′(x)g′(x)/f′(x)g(x)+f(x)g″(x)/f′(x)g(x)=0。
由①得f″(x)/f′(x)+2g′(x)/g(x)-f(x)g″(x)/f(x)g′(x)=0,则f″(x)/f′(x)+2g′(x)/g(x)=g″(x)/g′(x)。
又由②得f″(x)/f′(x)-f′(x)/f(x)=g″(x)/g′(x)-g′(x)/g(x)。
解析：暂无解析
第23题：

单选题
设f（x）为偶函数，g（x）为奇函数，则下列函数中为奇函数的是（　　）。[2018年真题]
A
f[g（x）]
B
f[f（x）]
C
g[f（x）]
D
g[g（x）]

正确答案： C
解析：
D项，令T（x）＝g[g（x）]。因为T（－x）＝g[g（－x）]＝g[－g（x）]＝－g[g（x）]，所以T（－x）＝－T（x），所以g[g（x）]为奇函数。
第24题：

单选题
设F（x），G（x）是f（x）的两个原函数，则下面的结论不正确的是（）。
A
F（x）+C也是f（x）的原函数，C为任意常数
B
F（x）=G（x）+C，C为任意常数
C
F（x）=G（x）+C，C为某个常数
D
F’（x）=G’（x）

正确答案： D
解析：由原函数的定义有F’（x）=f（x），G’（x）=f（x），因此（D）正确，而（F（x）+C）’=f（x），因此（A）正确，F（x）=G（x）+C，C应为某个常数，因此（C）正确而（B）不正确。

设 A 为方阵, f（x), g（x)为多项式, B = f（A), C = g（A), 则BC = CB.

题目

相似考题

参考答案和解析

更多“设 A 为方阵, f（x), g（x)为多项式, B = f（A), C = g（A), 则BC = CB.”相关问题

相关内容