在MATLAB里，10阶单位矩阵可以很简单地表示为

题目

在MATLAB里，10阶单位矩阵可以很简单地表示为

相似考题

1.n阶单位矩阵的特征值都是1。()此题为判断题(对，错)。

2.在matlab中对矩阵A的第2行第1列赋值为8可用A(1,2)=8表示。()

3.多项式在matlab中表示为向量形式，可用matlab中的多项式函数求多项式的根，多项式乘积等。()

4.在matlab中虚数表示为i,j。()

更多“在MATLAB里，10阶单位矩阵可以很简单地表示为”相关问题

  • 第1题：

    设a为N阶可逆矩阵，则（ ）.

    A.若AB=CB，则a=C：
    B.
    C.A总可以经过初等变换化为单位矩阵E：
    D.以上都不对.


    答案：C
    解析：

  • 第2题：

    与n阶单位矩阵E相似的矩阵是

    A.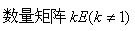
    B.对角矩阵D（主对角元素不为1）
    C.单位矩阵E
    D.任意n阶矩阵A


    答案：C
    解析：

  • 第3题：

    设a为N阶可逆矩阵，则（ ）.

    A.若AB=CB，则a=C
    B.
    C.A总可以经过初等变换化为单位矩阵E
    D.以上都不对


    答案：C
    解析：

  • 第4题：

    设n阶实对称矩阵A的秩为r，且满足，求 ①二次型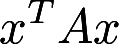的标准形； ②行列式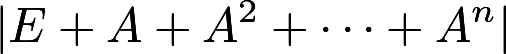的值，其中E为单位矩阵


    答案：
    解析：

  • 第5题：

    设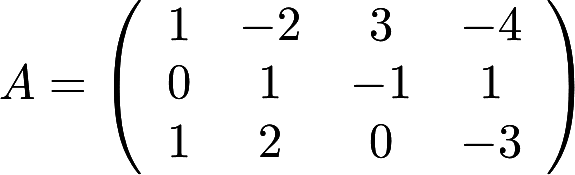，E为3阶单位矩阵（1）求方程组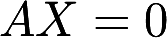的一个基础解系； （2）求满足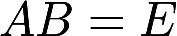的所有矩阵B


    答案：
    解析：

  • 第6题：

    设α为三维单位列向量，E为三阶单位矩阵，则矩阵E-αα^T的秩为________.


    答案：
    解析：

  • 第7题：

    设A为n阶非零矩阵，E为n阶单位矩阵。若A3=0，则( )。

    A.E－A不可逆，E+A不可逆
    B.E—A不可逆。E+A可逆
    C.E—A可逆。E+A可逆
    D.E—A可逆。E十A不可逆

    答案：C
    解析：
    (层_A)(E“+A2)=E-A3趣，(E+A)(E_A+A：)趣+A3翘，故E-A，层+A均可逆。

  • 第8题：

    关于Matlab，以下说法错误的是（）。

    • A、Matlab拥有强大的工具箱，可以方便地用于进行数值计算方法的程序设计
    • B、Matlab的数学可视化能力，使其对数值问题的近似解及误差给予图形解释
    • C、Matlab程序为编译执行，所以速度较快
    • D、Matlab由美国的MathWorks公司于1984年推出

    正确答案:C

  • 第9题：

    可以产生由Z2上n阶线性常系数齐次递推关系式的矩阵A称为什么？（）

    • A、乘方矩阵
    • B、列矩阵
    • C、单位矩阵
    • D、生成矩阵

    正确答案:D

  • 第10题：

    问答题
    设A是n阶矩阵，且满足Am＝E，其中m为整数，E为n阶单位矩阵。令将A中的元素aij换成它的代数余子式Aij而成的矩阵为A(～)，证明：（A(～)）m＝E。

    正确答案：
    因为Am=E,所以,Am,=,A,m=1,,A,=1≠0,即矩阵A可逆。
    由题知A(~)=(A*)T,其中A*为A的伴随矩阵。所以有(A(~))m=[(A*)T]m=[(,A,A-1)T]m=[(A-1)T]m=[(Am)-1]T=E。
    解析： 暂无解析

  • 第11题：

    填空题
    设A为n阶方阵，E为n阶单位矩阵，且A2＝A，则（A－2E）－1＝____。

    正确答案： -(A+E)/2
    解析：
    由题设A2＝A有，A2－A－2E＝（A－2E）（A＋E）＝－2E，即（A－2E）[－（A＋E）/2]＝E，所以有（A－2E）－1＝－（A＋E）/2。

  • 第12题：

    单选题
    可以产生由Z2上n阶线性常系数齐次递推关系式的矩阵A称为什么？（）
    A

    乘方矩阵

    B

    列矩阵

    C

    单位矩阵

    D

    生成矩阵


    正确答案： D
    解析： 暂无解析

  • 第13题：

    n阶方阵A,B,C满足ABC=E，其中E为单位矩阵，则必有（ ）.

    A.ACB=E
    B.CBA=E
    C.BAC=E
    D.BCA=E

    答案：D
    解析：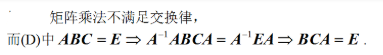

  • 第14题：

    设A，B，C均为n阶矩阵，E为n阶单位矩阵，若B=E+AB，C=A+CA，则B-C=



    A.E
    B.-E
    C.A
    D.-A

    答案：A
    解析：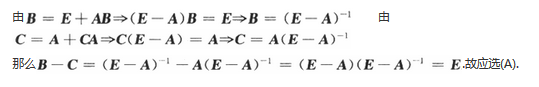

  • 第15题：

    已知4阶矩阵A~B，A的特征值为3,4,5,6，E为4阶单位矩阵，则|B-E|=（ ）

    A.20
    B.60
    C.120
    D.360

    答案：C
    解析：

  • 第16题：

    设A为n阶非奇异矩阵，α为n维列向量，b为常数.记分块矩阵.其中A*是矩阵A的伴随矩阵，E是n阶单位矩阵. （1）计算并化简PQ； （2）证明：矩阵Q可逆的充分必要条件是.


    答案：
    解析：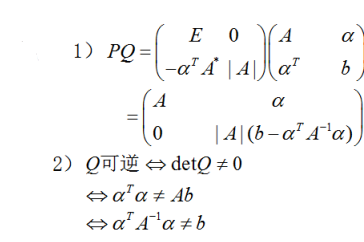

  • 第17题：

    设A=，E为三阶单位矩阵.
    　　(Ⅰ)求方程组Ax=0的一个基础解系；
    　　(Ⅱ)求满足AB=E的所有矩阵B.


    答案：
    解析：
    【分析】(Ⅰ)是基础题，化为行最简即可.
    关于(Ⅱ)中矩阵B，其实就是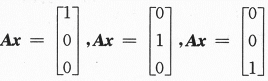三个方程组的求解问题.
    【解】(Ⅰ)对矩阵A作初等行变换，得

  • 第18题：

    设A为n阶非零矩阵，E为n阶单位矩阵，若A^3=O，则



    A.AE-A不可逆，E+A不可逆
    B.E-A不可逆，E+A可逆
    C.E-A可逆，E+A可逆
    D.E-A可逆，E+A不可逆

    答案：C
    解析：
    判断矩阵A可逆通常用定义，或者用充要条件行列式｜A｜≠0(当然｜A｜≠0又有很多等价的说法).因为(E-A)(E+A+A^2)=E-A^3=E，(E+A)(E-A+A^2)=E+A^3=E，所以，由定义知E-A，E+A均可逆.故选(C).

    【评注】本题用特征值也是简捷的，由A^3=O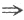A的特征值λ=0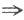E-A(或E+A)特征值均不为0｜E-A｜≠0(或｜E+A｜≠0)E-A(或E+A)可逆

  • 第19题：

    在MATLAB命令窗口中的“>>”标志为MATLAB的（）提示符，“│”标志为（）提示符


    正确答案:命令行;输入

  • 第20题：

    数据结构里，在算法时间复杂度中，O（nn）表示（）。

    • A、常数阶
    • B、线性阶
    • C、平方阶
    • D、立方阶

    正确答案:C

  • 第21题：

    填空题
    设n维向量α(→)＝（a，0，…，0，a）T，a＜0，E为n阶单位矩阵，矩阵A＝E－α(→)α(→)T，B＝E＋α(→)α(→)T/a，且B为A的逆矩阵，则a＝____。

    正确答案： -1
    解析：
    由矩阵B是矩阵A的逆矩阵，所以有AB＝E。从而（E－α(→)α(→)T）（E＋α(→)α(→)T/a）＝E－α(→)α(→)T＋α(→)α(→)T/a－α(→)（α(→)Tα(→)）α(→)T/a＝E，即α(→)α(→)T（1/a－1－2a2/a）＝0。
    由于α(→)α(→)T≠0，故1/a－1－2a2/a＝0，又因a＜0，可得a＝－1。

  • 第22题：

    单选题
    设A为n阶方阵，E为n阶单位矩阵，且A2＝A，则（A－2E）－1＝（　　）。
    A

    （A＋E）/2

    B

    －（A＋E）/2

    C

    （A－E）/2

    D

    －（A－E）/2


    正确答案： C
    解析：
    由题设A2＝A有，A2－A－2E＝（A－2E）（A＋E）＝－2E，即（A－2E）[－（A＋E）/2]＝E，所以有（A－2E）－1＝－（A＋E）/2。

  • 第23题：

    单选题
    数据结构里，在算法时间复杂度中，O（n）表示（）。
    A

    常数阶

    B

    线性阶

    C

    平方阶

    D

    立方阶


    正确答案： D
    解析： 暂无解析

  • 第24题：

    单选题
    设A为n阶方阵，E为n阶单位矩阵，且A2＝A，则（A－2E）－1＝（　　）。
    A

    A＋2E

    B

    A＋E

    C

    （A＋E）/2

    D

    －（A＋E）/2


    正确答案： A
    解析：
    由题设A2＝A有，A2－A－2E＝（A－2E）（A＋E）＝－2E，即（A－2E）[－（A＋E）/2]＝E，所以有（A－2E）－1＝－（A＋E）/2。

相关内容