某银行工会为丰富职工精神文化生活,在充满丰收喜悦、秋高气爽的金秋十月,举办了职工运动会。本届职运动会共有77 名职工参加保龄球、篮球、游泳、拔河、羽毛球、乒乓球等6 项比赛,由于比赛时间有限,每名职工只能参加一项比赛,如果每项比赛参加的人数不同,请问参加人数最多的比赛至少有多少人参加?( )。 A.12 B.15 C.16 D.13
题目
某银行工会为丰富职工精神文化生活,在充满丰收喜悦、秋高气爽的金秋十月,举办了职工运动会。本届职运动会共有77 名职工参加保龄球、篮球、游泳、拔河、羽毛球、乒乓球等6 项比赛,由于比赛时间有限,每名职工只能参加一项比赛,如果每项比赛参加的人数不同,请问参加人数最多的比赛至少有多少人参加?( )。
A.12
B.15
C.16
D.13
B.15
C.16
D.13
相似考题
更多“某银行工会为丰富职工精神文化生活,在充满丰收喜悦、秋高气爽的金秋十月,举办了职工运动会。本届职运动会共有77 名职工参加保龄球、篮球、游泳、拔河、羽毛球、乒乓球等6 项比赛,由于比赛时间有限,每名职工只能参加一项比赛,如果每项比赛参加的人数不同,请问参加人数最多的比赛至少有多少人参加?( )。 ”相关问题
-
第1题:
一个班级组织跑步比赛,共设100米、200米、400米三个项目。班级有50人,报名参加100米比赛的有27人,参加200米比赛的有25人,参加400米比赛的有21人。如果每人最多只能报名参加2项比赛,那么该班最多有多少人未报名参赛A.11
B.12
C.13
D.14答案:C解析:第一步,判断本题为容斥问题,需要结合最值思维解题。第二步,班级总数为50人,要想使未报名的最多,反向构造报名的人数最少。报名人次一定,则需要每人报名次数最多。由题意每人都可以最多报名2项,那么报名人数最少为(27+25+21)÷2=36.5,最少36.5,取整为37人。第三步,未报名人数为50-37=13人。因此,选择C选项。 -
第2题:
一次运动会上,赛前报名准备参加的男女运动员的人数之比为23:12。实际比赛时,有两名男运动员和三名女运动员因故没有参加比赛,使得实际参加比赛的男、女运动员的人数之比变为2:1。问实际参加比赛的运动员共多少名?()
A.135
B.140
C.150
D.160答案:A解析:方法一,设实际参加的女运动员有x名,则实际参加的男运动员有2x名,实际参加比赛的运动员有3x名。由题意,得(2x+2):(x+3)=23:12,解得x=45,故实际参加比赛的运动员有45×3=135名.选择A。
方法二,依题意可知实际参加比赛的运动员人数应该是3的倍数,选项中只有A、C符合。
假设实际参加比赛的运动员为135名,则男、女运动员分别为90、45名,准备参加的男女运动员分别为92、48名,人数比为92:48=23:12,符合题意,选择A;
假设实际参加比赛的运动员为150名,则男、女运动员分别为100、50名,准备参加的男女运动员分别为102、53名,而102、53不是23、12的倍数,不符合题意,排除C。 -
第3题:
在本届运动会上,所有参加自由泳比赛的运动员都参加了蛙泳比赛。再加入以下哪项陈述,可以推出“有些参加蝶泳比赛的运动员没有参加自由泳比赛”?( )
A.所有参加蝶泳比赛的运动员也参加了蛙泳比赛
B.有些参加蛙泳比赛的运动员参加了蝶泳比赛
C.有些没有参加蛙泳比赛的运动员参加了蝶泳比赛
D.有些没有参加蝶泳比赛的运动员也没有参加蛙泳比赛答案:C解析:所有参加自由泳比赛的运动员都参加了蛙泳比赛,而有些没有参加蛙泳比赛的运动员参加了蝶泳比赛,由这两个命题可以推出,有些没有参加自由泳比赛的运动员参与了蝶泳比赛。即题干所求,故选C。 -
第4题:
孔智、孟睿、荀慧、庄聪、墨灵、韩敏等6人组成一个代表队参加某次棋类大赛,其中两人参加围棋比赛,两人参加中国象棋比赛,还有两人参加国际象棋比赛。有关他们具体参加比赛项目的情况还需满足以下条件:
(1)每位选手只能参加一个比赛项目;
(2)孔智参加围棋比赛,当且仅当,庄聪和孟睿都参加中国象棋比赛;
(3)如果韩敏不参加国际象棋比赛,那么墨灵参加中国象棋比赛;
(4)如果荀慧参加中国象棋比赛,那么庄聪不参加中国象棋比赛;
(5)荀慧和墨灵至少有一人不参加中国象棋比赛。
根据题干信息,以下哪项可能为真?A.庄聪和韩敏参加中国象棋比赛
B.韩敏和荀慧参加中国象棋比赛
C.孔智和孟睿参加围棋比赛
D.墨灵和孟睿参加围棋比赛答案:D解析:该题的参考答案是D.该题可用排除法,A说韩和庄参加中国象棋比赛,依据条件(3),韩敏参加中国象棋就是没有参加国际象棋比赛,那么墨灵也得参加中国象棋比赛,这就有三个人要参加中国象棋比赛了,不符合题干所说的两个人参加的信息,所以A不可能为真。B说韩和荀参加中国象棋比赛,同样依据题干条件(3)可知韩、荀墨三人都
得参加中国象棋比赛,所以B也不可能真。C说孔和孟参加围棋比赛,但依据题干条件(2)可知,孔参加围棋比赛则孟不能参加围棋比赛,所以C不可能为真。E说韩和孔参加围棋比赛,但依据条件(2)庄和孟都参加中国象棋比赛,又依据条件(3)墨灵也参加中国象棋比赛,这样就有三个人得参加中国象棋比赛,不合题干两人参加的信息,所以不可能为真,A.B、C和E都不可能为真,正确答案只能是D. -
第5题:
某班级在学校举行的春季运动会中组织同学报名参加拔河和100米赛跑两项比赛。只有2人同时参加了这两项运动。已知该班级参加拔河比赛的运动员与该班级运动员总人数之比为7:10,且只参加拔河比赛的人数是只参加100米赛跑的人数的2倍。则只参加拔河比赛的运动员有( )人。A.10
B.12
C.14
D.16答案:B解析:
-
第6题:
以下哪些情况不参加比赛应判该队弃权而告负()
- A、在篮球比赛中如果球队场上队员人数少于2名时
- B、在预定的比赛时间开始后15分钟,球队不到场或不能使5名队员入场准备比赛
- C、它的行为阻碍比赛继续进行
- D、在主裁判员通知后拒绝比赛
正确答案:B,C,D -
第7题:
维保公司支持职工运动会、主持人大赛、歌咏比赛等,提升职工的文化生活。
正确答案:正确 -
第8题:
如果小张和小王都参加比赛,那么小李也参加比赛。现在小李没有参加比赛,那么请问还有谁也没有参加比赛()
- A、小张
- B、小王
- C、小张和小王都没有参加比赛
- D、无法确定
正确答案:D -
第9题:
某单位组织的羽毛球男单比赛共有48名选手报名参加,比赛采用淘汰赛制,在比赛中负一场的选手即被淘汰,直至决出最后的冠军,如每名选手每天最多参加一场比赛,则比赛至少需要举行几天?
- A、4
- B、5
- C、6
- D、7
正确答案:C -
第10题:
单选题为增强职工的锻炼意识,某单位举行了踢毽子比赛,比赛时长为1分钟,参加比赛的职工平均每人踢了76个。已知每人至少踢了70个,并且其中又一人踢了88个,如果不把该职工计算在内,那么平均每人踢了74个,则踢得最快的职工最多踢了多少个?()A88
B90
C92
D94
正确答案: D解析: 暂无解析 -
第11题:
单选题有100人参加运动会的三个比赛项目,每人至少参加一项,其中未参加跳远的有50人,未参加跳高的有60人,未参加赛跑的有70人。那么至少有( )人参加了不止一个项目的比赛。A7
B10
C15
D20
正确答案: B解析: -
第12题:
单选题一个班级组织跑步比赛,共设 100 米、200 米、400 米三个项目。班级有 50 人,报名参加 100 米比赛的有27 人,参加 200 米比赛的有 25 人,参加 400 米比赛的有 21 人。如果每人最多只能报名参加 2 项比赛,那么该班最多有多少人未报名参赛?A11
B12
C13
D14
正确答案: B解析: -
第13题:
某工会为丰富职工生活,组织77名职工参加6项业余活动,所有职工都参加了,且由于活 动时间相同,每个职工只能参加一项活动。如果每项活动参加的人数不同,问参加人数最 多的活动至少有多少人参加?( )
A. 12
B. 13
C. 15
D. 16答案:D解析: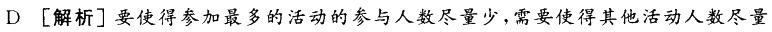

-
第14题:
某机关举行职工秋季田径运动会。已知:所有报名参加短跑比赛的职工都报名参加铅球比赛,所有报名参加跳远比赛的职工都没有报名参加铅球比赛,报名参加跳高比赛的职工也都报名参加了跳远比赛,而没有报名参加跳高比赛的职工也没有报名参加长跑比赛。
根据以上陈述,可以得出以下哪项?A.有的报名参加铅球比赛的职工没有报名参加短跑比赛
B.有的报名参加跳高比赛的职工没有参加长跑比赛
C.所有报名参加跳远比赛的职工都报名参加长跑比赛
D.所有报名参加短跑比赛的职工都没有报名参加长跑比赛答案:D解析:第一步,确定题型。
根据题干关键词“所有”,确定为集合推理。
第二步,翻译题干。
①所有报名短跑的都报名了铅球(短跑→铅球);
②所有报名跳远的都没有报名铅球(跳远→?铅球);
③所有报名跳高的都报名了跳远(跳高→跳远);
④所有没有报名跳高的都没有报名长跑(?跳高→?长跑)。
第三步,进行推理。
A项:将①进行换位推理可得“有的报名铅球的报名了短跑”,根据“有的是”无法必然推出“有的不是”,该项无法推出;
B项:将④进行逆否可得:所有报名长跑的都报名了跳高,再将其进行换位推理可得“有的报名跳高的报名了长跑”,根据“有的是”无法必然推出“有的不是”,该项无法推出;
C项:将④进行逆否可得:长跑→跳远,“所有报名跳远”是对其“肯后”,根据肯后推不出必然结论,该项无法推出;
D项:将①②③④进行递推可得:短跑→?长跑,即“所有报名短跑的都没有报名长跑”,该项可以推出。
因此,选择D选项。 -
第15题:
孔智、孟睿、荀慧、庄聪、墨灵、韩敏等6人组成一个代表队参加某次棋类大赛,其中两人参加围棋比赛,两人参加中国象棋比赛,还有两人参加国际象棋比赛。有关他们具体参加比赛项目的情况还需满足以下条件:(1)每位选手只能参加一个比赛项目;(2)孔智参加围棋比赛,当且仅当,庄聪和孟睿都参加中国象棋比赛;(3)如果韩敏不参加国际象棋比赛,那么墨灵参加中国象棋比赛;(4)如果荀慧参加中国象棋比赛,那么庄聪不参加中国象棋比赛;(5)荀慧和墨灵至少有一人不参加中国象棋比赛。如果荀慧参加中国象棋比赛,那么可以得出以下哪项?A.庄聪和墨灵都参加围棋比赛。
B.孟睿参加围棋比赛
C.孟睿参加国际象棋比赛。
D.墨灵参加国际象棋比赛。
E.韩敏参加国际象棋比赛。答案:E解析:苟慧参加中国象棋比赛,结合(5)推出墨灵不参加中国象棋比赛,再结合(3)可推出韩敏参加国际象棋比赛。 -
第16题:
孔智、孟睿、荀慧、庄聪、墨灵、韩敏等6人组成一个代表队参加某次棋类大赛,其中两人参加围棋比赛,两人参加中国象棋比赛,还有两人参加国际象棋比赛。有关他们具体参加比赛项目的情况还需满足以下条件:(1)每位选手只能参加一个比赛项目;(2)孔智参加围棋比赛,当且仅当,庄聪和孟睿都参加中国象棋比赛;(3)如果韩敏不参加国际象棋比赛,那么墨灵参加中国象棋比赛;(4)如果荀慧参加中国象棋比赛,那么庄聪不参加中国象棋比赛;(5)荀慧和墨灵至少有一人不参加中国象棋比赛。如果庄聪和孔智参加相同的比赛项目,且孟睿参加中国象棋比赛,那么可以得出以下哪项?A.墨灵参加国际象棋比赛。
B.庄聪参加中国象棋比赛。
C.孔智参加围棋比赛。
D.荀慧参加围棋比赛。
E.韩敏参加中国象棋比赛。答案:D解析:判断题。根据庄聪和孔智参加比赛相同,再根据题干一个比赛只有两人参加,可推出庄聪和孟睿不同,再结合(2)可知孔智不能参加围棋比赛;根据孟睿参加中国象棋比赛,可推出庄和孔不能参加中国象棋比赛,所以庄和孔都参加国际象棋比赛。再根据(4)可推出苟慧不能参加中国象棋比赛,所以只能荀慧参加围棋比赛。 -
第17题:
张三、李四、王五三人分别参加在甲、乙、丙地举行的羽毛球、游泳、划船三项比赛,比赛中他们都得了冠军。已知张三没到丙地去划船,王五没参加在乙举行的游泳比赛,划船冠军不是王五。请问,游泳冠军是:( )。A、张三
B、李四
C、王五
D、未知数答案:A解析:根据题干信息逐一分析。
①张三、李四、王五三人分别参加在甲、乙、丙地举行的羽毛球、游泳、划船三项比赛,且都得了冠军;
②张三没到丙地去划船;
③王五没参加在乙举行的游泳比赛;
④划船冠军不是王五。 根据条件③可知,王五不是游泳冠军;根据条件④可知王五不是划船冠军,那么王五只能是羽毛球冠军。
根据条件②可知,张三不是划船冠军,那么张三只能是游泳冠军,李四则是划船冠军。 -
第18题:
健身健美操比赛参加人数为5-6人。
正确答案:错误 -
第19题:
有10队参加篮球比赛,先分为两小组进行循环赛,然后两小组1、2名同一天进行同名次决赛,每天每队只能进行一场比赛。请问小组赛共有多少轮次?比赛需要几天?比赛总场次多少?(要求列出计算式)
正确答案: 小组比赛轮次=倚数队数=10/2=5
比赛天数=小组轮次+决赛轮次=5+1=6
比赛总场次=小组场次+决定场次=N×(N-1)/2×2+2=5×(5-1)/2×2+2=22 -
第20题:
88名学生参加运动会,参加游泳比赛的有23人,参加田径比赛的有33人,参加球类比赛的有54人,既参加游泳比赛又参加田径比赛的有5人,既参加田径比赛又参加球类比赛的有16人。已知每名学生最多可参加两项比赛,问只参加田径比赛的有多少人()
- A、20
- B、17
- C、15
- D、12
正确答案:D -
第21题:
为增强职工的锻炼意识,某单位举行了踢毽子比赛,比赛时长为1分钟。参加比赛的职工平均每人踢了76个,已知每人至少踢了70个,并且其中一人88个,如果不把该职工计算在内,那么平均每人踢了74个。则踢得最快的职工最多踢了多少个()。
- A、88
- B、90
- C、92
- D、94
正确答案:D -
第22题:
判断题维保公司支持职工运动会、主持人大赛、歌咏比赛等,提升职工的文化生活。A对
B错
正确答案: 错解析: 暂无解析 -
第23题:
多选题以下哪些情况不参加比赛应判该队弃权而告负()A在篮球比赛中如果球队场上队员人数少于2名时
B它的行为阻碍比赛继续进行
C在预定的比赛时间开始后15分钟,球队不到场或不能使5名队员入场准备比赛
D在主裁判员通知后拒绝比赛
正确答案: D,C解析: 暂无解析
