某大学某班学生总数为32人。在第一次考试中有26人及格，在第二次考试中有24人及格。若两次考试中，都没有及格的有4人，那么两次考试都及格的人数是（　　）。A．22 B．18 C．28 D．26

题目
某大学某班学生总数为32人。在第一次考试中有26人及格，在第二次考试中有24人及格。若两次考试中，都没有及格的有4人，那么两次考试都及格的人数是（　　）。


A．22 B．18
C．28 D．26
相似考题

1.如果甲和乙都没有考试及格的话，那么丙就一定及格了。上述前提再增加以下哪项，就可以推出甲考试及格了的结论?A．丙及格了。B．丙没有及格。C．乙没有及格。D．乙和丙都没有及格。

2.第 40 题 六年级一班有学生50人，第一次考试有38人及格，第二次考试有24人及格，其中两次考试都及格的有20人，两次考试都不及格的有多少人?A．6B．12C．8D．10

3.某班学生不到50人,在一次考试中,有1／7人得优,1／3人得良,1／2人及格,其余的均不及格,那么不及格某班学生不到５０人，在一次考试中，有１／７人得优，１／３人得良，１／２人及格，其余的均不及格，那么不及格的人数是 。Ａ．１ Ｂ．２ Ｃ．３ Ｄ．４

4.如果秦川考试及格了，那么钱华、孙勋和沈楠肯定也都及格了。 如果上述断定是真的，那么，以下哪项也是真的？（ ）A．如果秦川考试没有及格，那么，钱、孙、沈三人中至少有一人没有及格B．如果秦川考试没有及格，那么，钱、孙、沈三人都没有及格C．如果孙勋考试没有及格，那么，秦川和沈楠不会都及格D．如果沈楠考试没有及格，那么，钱华和孙勋不会都及格

更多“某大学某班学生总数为32人。在第一次考试中有26人及格，在第二次考试中有24人及格。若两次考试中，都没有及格的有4人，那么两次考试都及格的人数是（　　）。 ”相关问题

  • 第1题：

    如果甲和乙考试都没有及格的话，那么丙就一定及格了。上述前提再增加以下 项，就可以推出“甲考试及格了”的结论。

    Ａ．丙及格了 Ｂ．乙和丙都没有及格 Ｃ．丙没有及格 Ｄ．乙和丙都及格了


    正确答案：B

  • 第2题：

    某大学某班学生总数为32人，在第一次考试中有26人及格，在第二次考试中有24人及格，若两次考试中，都没有及格的有4人，那么两次考试都及格的人数是( )。

    A．22

    B．18

    C．28

    D．26


    正确答案：A
    A  [解析]都没有及格的有4人，则至少有一次考试及格的人数为32-4=28，两次考试及格的总人数次是26+24=50，所以两次考试都及格的人数是50-28=22，故选A。

  • 第3题：

    某班有40人，在期末考试中，语文有35人及格，数学有32人及格，外语有33人及格，不及格的人中没有只有一门不及格的，其中有2人全都不及格，有4人语文和数学都不及格，有6人数学和外语都不及格，有多少人语文和外语都不及格?（ ）

    A．2

    B．3

    C．4

    D．5


    正确答案：B
    (1)全班共40人。(2)设语文和外语都不及格的为X人。由于有4人语文和数学都不及格的减去2个都不及格的，有2个仅语文和数学不及格而外语及格，由于语文和外语都不及格的为％人，减去2个都不及格的为(x－2)个仅语文和外语不及格而数学及格的，全班共40人，即40=35+2+(x－2)+2，解得x=3，故选B。

  • 第4题：

    六年级一班有学生50人，第一次考试有38人及格，第二次考试有24人及格，其中两次考试都及格的有20人，两次考试都不及格的有多少人：

    A6
    B12
    C8
    D10


    答案：C
    解析：
    由两集合容斥原理公式得两次都不及格的人数为50-(38+24-20)=8人。故正确答案为C。

    两集合容斥原理公式：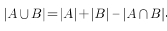

  • 第5题：

    某班学生不到50人，在一次考试中，有1/7人得优，1/3人得良，1/2人及格，其余的均不及格，那么不及格的人数是（ ）。


    A. 1
    B. 2
    C. 3
    D. 4

    答案：A
    解析：
    解题指导： 通过题干可知，该班级最少人数应为7、3、2的最小公倍数，又因为不能超过50人，所以该班人数为7×3×2=42人。那么不及格的人数为1。故答案为A。

  • 第6题：

    如果小明和小新都没有考试及格的话.那么小敏就一定及格了。要推出“小明考试及格了”的结论.则需要再加上以下哪项条件?()

    A.小敏及格了
    B.小敏没有及格
    C.小新没有及格
    D.小新和小敏都没有及格

    答案：D
    解析：
    【知识点】教师基本能力——逻辑思维能力
    题干是一个前件为联言命题的充分条件假言命题。要想推出“小明考试及格”，则需要否定后件。即“小敏没有及格”;根据推理规则，推出否定的前件，即“小明或小新考试及格”;相容选言命题。否定一个选言肢则可肯定另一个选言肢，即要想推出小明考试及格，需要新考试不及格。故答案选D。

  • 第7题：

    下列判断与“这次考试可能会及格”为矛盾关系判断的有（）。

    • A、这次考试可能不会及格
    • B、这次考试必然不及格
    • C、这次考试不必然会及格
    • D、这次考试不可能不及格

    正确答案:B

  • 第8题：

    某班有学生50人，有26人在第一次考试中得优，有21人在第二次考试中得优，有17人在两次考试中都没有得优，那么两次考试都得优的学生人数是（）

    • A、11.0
    • B、12.0
    • C、13.0
    • D、14.0

    正确答案:D

  • 第9题：

    甲、乙、丙、丁是同班同学。甲说：“我班同学考试都及格了。”乙说：“丁考试没及格。”丙说：“我班有人考试没及格。”丁说：“乙考试也没及格。”已知只有一人说假话，则可推断以下哪项断定是真的（）

    • A、说假话的是甲，乙考试没及格
    • B、说假话的是乙，丙考试没及格
    • C、说假话的是丙，丁考试没及格
    • D、说假话的是丁，乙考试及格了

    正确答案:A

  • 第10题：

    甲、乙、丙、丁是同班同学。甲说："我班同学考试都及格了。"乙说："丁考试没及格。"丙说："我班有人考试没及格。"丁说："乙考试也没及格。"已知只有一个人说假话，则可推断以下哪项断定是真的（）。

    • A、说假话的是甲，乙考试没及格
    • B、说假话的是乙，丙考试没及格
    • C、说假话的是丙，丁考试没及格
    • D、说假话的是丁，乙考试及格了

    正确答案:A

  • 第11题：

    单选题
    下列判断与“这次考试可能会及格”为矛盾关系判断的有（）。
    A

    这次考试可能不会及格

    B

    这次考试必然不及格

    C

    这次考试不必然会及格

    D

    这次考试不可能不及格


    正确答案： B
    解析： 暂无解析

  • 第12题：

    多选题
    当判断（）为真时，判断“班上同学考试都及格”为假。
    A

    并非班上同学考试都不及格

    B

    班上同学考试不都及格

    C

    班上没有一个同学考试不及格

    D

    并非班上有的同学考试及格


    正确答案： B,A
    解析： 暂无解析

  • 第13题：

    某大学某班学生总数是32人，在第一次考试中有26人及格，在第二次考试中有24人及格，若两次考试中，都没及格的有4人，那么两次考试都及格的人数是(  )

    A.22        B.18       C.28      D.26


    设两次考试都及格的人数是X人,则及格人数中仅第一次及格的是26-X人,仅第二次及格的人数是24-X人.
    由题知不及格人数中仅第一次不及格的是32-26-4=2人,仅第二次不及格的是32-24-4=4人.
    仅第一次及格人数+仅第二次及格人数+两次都及格人数+仅第一次不及格人数+仅第二次不及格人数+两次都不及格人数=全班总人数,即(26-X)+(24-X)+X+2+4+4=32,得X=28

  • 第14题：

    如果小张考试及格并且大田考试不及格，则小娜考试一定不及格。如果以上命题是真的，那么，再加上什么前提，可以得出结论：大田考试及格了（ ）

    A．小张考试及格而大田考试不及格

    B．小张与小娜考试都不及格

    C．小张与小娜考试都及格了

    D．小张考试不及格而小娜考试及格


    正确答案：C
     题干是以一个充分条件假言命题“如果p并且非q，那么非r”作前提得出结论“q”，需要补充前提。观察题干可以发现，结论“q”是充分条件的前件中的一部分内容。充分条件假言推理通过否定后件可以得到关于前件内容的否定，因此，首先应该否定后件“非r”，即非非r，也即r，“小娜考试及格了”，可以得到，并非“p并且非q”，即“非p或者q”，“小张没有及格或者大田及格了”，这是一个选言命题，它的有效推理式是否定肯定式，即通过否定一个选言支(即非非p)来肯定另一个选言支(即q)，要想肯定“大田及格了”必须否定“小张没有及格”，即“小张及格了”；所以，要想得到“大田及格了”的结论，需要补充“小娜及格了”和“小张及格了”，即选项C。

  • 第15题：

    ：某大学某班学生总数为32人。在第一次考试中有26人及格，在第二次考试中有24人及格。若两次考试中，都没有及格的有4人，那么两次考试都及格的人数是（ ）。

    A．22 B．18

    C．28 D．26


    正确答案：A

    由题意知第一次不及格的有6人，第二次不及格的有8人，又已知两次都不及格的人有4人，则两次考试刚好及格一次的人数为6＋8－4＝10（人），则两次都及格的人数为32－（6＋8－4）＝22（人），故答案为A。

  • 第16题：

    某次数学考试结束后，甲班班长和学习委员一起对考试成绩进行了预测，具体如下：
    1．有人考试没及格；
    2．有人考试及格了；
    3．班长考试没及格。
    成绩公布后，发现三句预测中只有一句话正确。可推知：

    A.甲班同学都没有及格
    B.甲班同学有人没及格
    C.学习委员考试及格了
    D.学习委员考试没及格

    答案：C
    解析：
    第一步，确定题型。
    题干有若干论断和真假限定，确定为真假推理。
    第二步，找关系。
    1.“有人考试没及格”和2.“有人考试及格了”为反对关系。
    第三步，看其余。
    根据反对关系的特性“两个有的，必有一真”及题干的真假限定，可知1、2之间必有一真，又因为“三句预测中只有一句话正确”，可知3为假，根据3为假，可得：班长考试及格了，根据班长考试及格了，可知：有人及格了，进而可知：2为真，1为假，即“有人考试没及格”为假，其矛盾命题则为真，即“甲班所有人考试都及格了”为真，由此可知，学习委员考试及格了。

  • 第17题：

    如果甲和乙都没有考试及格的话,那么丙就一定及格了。上述前提再增加以下哪项,就可以推出“甲考试及格了”的结论?

    A.丙及格了
    B.丙没有及格
    C.乙没有及格
    D.乙和丙都没有及格
    E.乙和丙都及格了

    答案：D
    解析：

  • 第18题：

    当命题（）为真时，命题“班上同学考试都及格”为假。

    • A、并非班上同学考试都不及格
    • B、班上有的同学考试不及格
    • C、班上同学并没都及格
    • D、班上同学都不及格
    • E、并非班上有的同学考试及格

    正确答案:B,C,D,E

  • 第19题：

    特殊培训考试分理论考试和实际操作考试。理论考试和实际操作考试（）视为考试合格。

    • A、理论考试及格
    • B、任一项考试及格
    • C、两项考试均及格

    正确答案:C

  • 第20题：

    当判断（）为真时，判断“班上同学考试都及格”为假。

    • A、并非班上同学考试都不及格
    • B、班上同学考试不都及格
    • C、班上没有一个同学考试不及格
    • D、并非班上有的同学考试及格
    • E、班上同学考试不都不及格

    正确答案:B,D

  • 第21题：

    当判断（）为真时，判断“班上同学考试都及格”为假。

    • A、并非班上同学考试都不及格
    • B、班上同学考试不都及格
    • C、班上没有一个同学考试不及格
    • D、并非班上有的同学考试及格

    正确答案:B,D

  • 第22题：

    如果甲和乙考试都没有及格的话，那么丙就一定及格了。上述前提再增加以下哪项，就可以推出“甲考试及格了”的结论（）

    • A、丙及格了
    • B、乙和丙都没有及格
    • C、丙没有及格
    • D、乙和丙都及格了

    正确答案:B

  • 第23题：

    多选题
    当判断（）为真时，判断“班上同学考试都及格”为假。
    A

    并非班上同学考试都不及格

    B

    班上同学考试不都及格

    C

    班上没有一个同学考试不及格

    D

    并非班上有的同学考试及格

    E

    班上同学考试不都不及格


    正确答案： B,C
    解析： “班上同学考试都及格”为假即SAP为假。 A、“并非班上同学考试都不及格”等值于SIP而SIP真SAP是可真可假所以错误； B、是一个SEP判断，由于SEP与SAP是不能同真所以SEP真即可断定SAP假所以正确； C、实际上就是一个SAP判断所以错误； D、等值于SEP与B相同所以正确； E、实际上是一个SAP判断所以错误。所以应选BD。

  • 第24题：

    多选题
    当命题（）为真时，命题“班上同学考试都及格”为假。
    A

    并非班上同学考试都不及格

    B

    班上有的同学考试不及格

    C

    班上同学并没都及格

    D

    班上同学都不及格

    E

    并非班上有的同学考试及格


    正确答案： C,D
    解析： 暂无解析

相关内容