设D为2≤x2+y2≤2x所确定的区域,则二重积分化为极坐标系下的二次积分时等于:
题目
设D为2≤x2+y2≤2x所确定的区域,则二重积分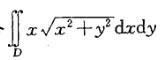 化为极坐标系下的二次积分时等于:
化为极坐标系下的二次积分时等于:

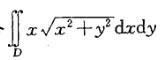 化为极坐标系下的二次积分时等于:
化为极坐标系下的二次积分时等于:

相似考题
更多“设D为2≤x2+y2≤2x所确定的区域,则二重积分化为极坐标系下的二次积分时等于: ”相关问题
-
第1题:
设二重积分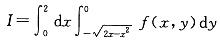 交换积分次序后,则I等于下列哪一式?
交换积分次序后,则I等于下列哪一式?
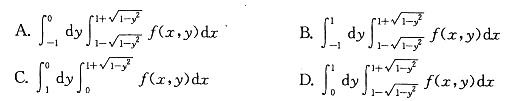 答案:A解析:提示:画出积分区域D的图形,再写出先x后y的积分表达式。如下:
答案:A解析:提示:画出积分区域D的图形,再写出先x后y的积分表达式。如下: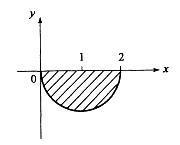

-
第2题:
化二重积分为极坐标系下的二次积分,则 等于下列哪一式?
等于下列哪一式?
 答案:D解析:提示:画出积分区域D的图形,确定γ和θ的取值。
答案:D解析:提示:画出积分区域D的图形,确定γ和θ的取值。
-
第3题:
设Ω是由:x2+y2+z2≤2z及z≤x2+y2所确定的立体区域,则Ω的体积等于: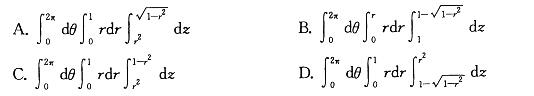 答案:D解析:提示:本题Ω是由球面里面部分和旋转拋物面外部围成的,立体在xOy平面上投影区域:x2 +y2≤1,利用柱面坐标写出三重积分。
答案:D解析:提示:本题Ω是由球面里面部分和旋转拋物面外部围成的,立体在xOy平面上投影区域:x2 +y2≤1,利用柱面坐标写出三重积分。
-
第4题:
设圆周曲线L:x2+y2=1取逆时针方向,则对坐标的曲线积分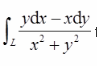
值等于( )。A.2π
B.-2π
C.π
D.0答案:B解析:采用三角函数代换法,令x=cosx,y=sinx。则: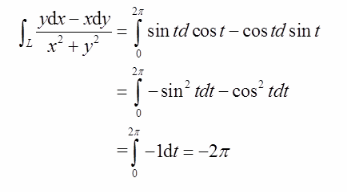
-
第5题:
设二重积分 交换积分次序后,则I等于下列哪式?
交换积分次序后,则I等于下列哪式?
 答案:A解析:提示:画出积分区域D的图形,再写出先x后y的积分表达式。如下:
答案:A解析:提示:画出积分区域D的图形,再写出先x后y的积分表达式。如下:

-
第6题:
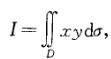 D是由y2=x及y=x-1所围成的区域,则化为二次积分后的结果为:
D是由y2=x及y=x-1所围成的区域,则化为二次积分后的结果为:
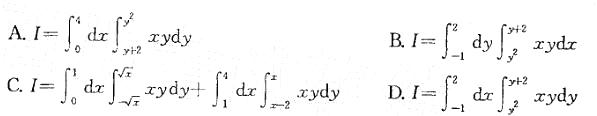 答案:B解析:提示:画出积分区域D的图形,求出交点坐标(4,2) ,(1,-1),再按先x后y的积分顺序化为二次积分。
答案:B解析:提示:画出积分区域D的图形,求出交点坐标(4,2) ,(1,-1),再按先x后y的积分顺序化为二次积分。 -
第7题:
曲线x2+y2=2x在点(1,1)处的切线方程为.答案:解析:【答案】y=1【考情点拨】本题考查了曲线上一点处的切线方程的知识点.
【应试指导】由x2+y2=2x,两边对x求导得2x+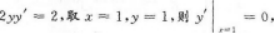
-
第8题:
设区域 ,计算二重积分
,计算二重积分 答案:解析:
答案:解析:
-
第9题:
将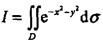 (其中D:x2+y2≤1)化为极坐标系下的二次积分,其形式为( )。
(其中D:x2+y2≤1)化为极坐标系下的二次积分,其形式为( )。
 答案:D解析:提示:
答案:D解析:提示: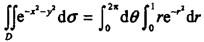 。
。 -
第10题:
设随机变量X服从参数为2的泊松分布,则E(2X)=()
正确答案:4 -
第11题:
设D={(x,y)|1≤x2+y2≤4},则二重积分的值是().
- A、3π
- B、4π
- C、5π
- D、14/3π
正确答案:D -
第12题:
单选题设z=f(x2+y2),其中f具有二阶导数,则等于().A2f’(x2+y2)
B4x2f(x2+y2)
C2’(x2+y2)+4x2f(x2+y2)
D2xf(x2+y2)
正确答案: D解析: 暂无解析 -
第13题:
Ω是由曲面z=x2+y2,y=x,y=0,z=1在第一卦限所围成的闭区域,f(x,y,z) 在Ω上连续,则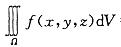 等于:
等于:
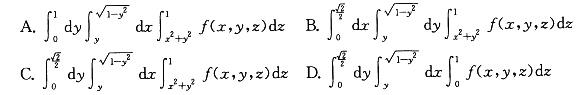 答案:C解析:提示:作出Ω的立体图形,并确定Ω在xOy平面上投影区域:Dxy:x2+y2 = 1,写出在直角坐标系下先z后x最后y的三次积分。
答案:C解析:提示:作出Ω的立体图形,并确定Ω在xOy平面上投影区域:Dxy:x2+y2 = 1,写出在直角坐标系下先z后x最后y的三次积分。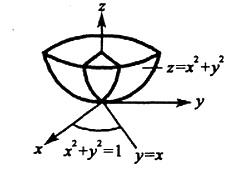
-
第14题:
 化为极坐标系下的二次积分时等于:
化为极坐标系下的二次积分时等于:
 答案:D解析:提示:画出积分区域D的图形,由x2+y2≥2得知在圆
答案:D解析:提示:画出积分区域D的图形,由x2+y2≥2得知在圆
-
第15题:
设D为圆域x2+y2≤4,则下列式子中哪一式是正确的? 答案:C解析:提示:化为极坐标系下的二次积分,面积元素为
答案:C解析:提示:化为极坐标系下的二次积分,面积元素为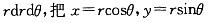 代入计算。
代入计算。 -
第16题:
若D是由x=0,y=0,x2+y2=1所围成在第一象限的区域,则二重积分
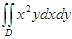
等于( )。
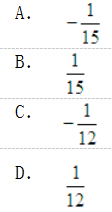 答案:B解析:采用极坐标法求二重积分,具体计算如下:
答案:B解析:采用极坐标法求二重积分,具体计算如下:
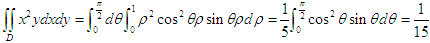
-
第17题:
设二重积分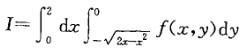 ,交换积分次序后,则I等于:
,交换积分次序后,则I等于:
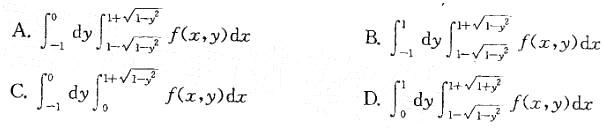 答案:A解析:解:本题考查二重积分交换积分次序方面的知识。解这类题的基本步骤:通过原积分次序画出积分区域的图形,得到积分区域;然后写出先x后y的积分表达式。
答案:A解析:解:本题考查二重积分交换积分次序方面的知识。解这类题的基本步骤:通过原积分次序画出积分区域的图形,得到积分区域;然后写出先x后y的积分表达式。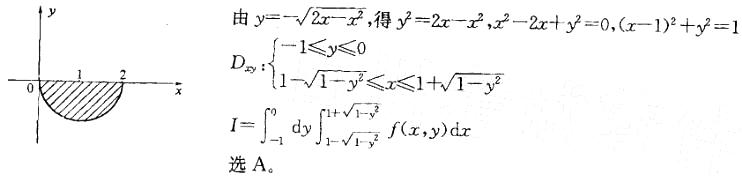
-
第18题:
 (其中D:x2+y2≤1)化为极坐标系下的二次积分,其形式为下列哪一式?
(其中D:x2+y2≤1)化为极坐标系下的二次积分,其形式为下列哪一式?
 答案:D解析:提示:化为极坐标系下的二次积分,面积元素dσ=rdrdθ,把x=rcosθ,y=rsinθ代入。
答案:D解析:提示:化为极坐标系下的二次积分,面积元素dσ=rdrdθ,把x=rcosθ,y=rsinθ代入。 -
第19题:
将二重积分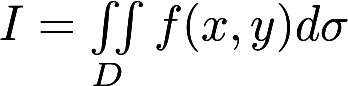 化为累次积分(两种形式), 其中D给定如下: D:
化为累次积分(两种形式), 其中D给定如下: D: 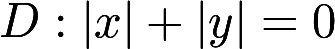 由所围之区域.答案:解析:
由所围之区域.答案:解析:
-
第20题:
在直角坐标系中,若平面区域D中虽有的点的坐标(x,y)均满足:0≤x≤6,0≤y≤6,|y-x|≤3,x2+y2≥9,则面积是( )
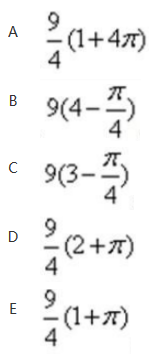 答案:C解析:
答案:C解析: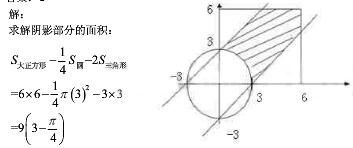
-
第21题:
设区域D为x2+y2≤4,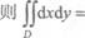 A.4π
A.4π
B.3π
C.2π
D.π答案:A解析: A为区域D的面积.由于D为x2+y2≤4表示圆域,半径为2,因此A=π×22=4π,所以选A.
A为区域D的面积.由于D为x2+y2≤4表示圆域,半径为2,因此A=π×22=4π,所以选A. -
第22题:
设z=f(x2+y2),其中f具有二阶导数,则等于().
- A、2f’(x2+y2)
- B、4x2f"(x2+y2)
- C、2’(x2+y2)+4x2f"(x2+y2)
- D、2xf"(x2+y2)
正确答案:C -
第23题:
单选题设D={(x,y)|1≤x2+y2≤4},则二重积分的值是().A3π
B4π
C5π
D14/3π
正确答案: D解析: 暂无解析
