某人的效用函数为U(C，R) =C-（12 -R）2，其中R是他每天拥有的闲暇时间，C为消费量。他每天有16小时可用在工作和闲暇上，每天有20元的非劳动收入。消费品的价格是每单位1元。工资为每小时10元，他将选择多少小时进行工作以获得最大效用？

第1题：

答案：

解析：

第2题：

答案：A

解析：

效用函数的一个常见形式为：

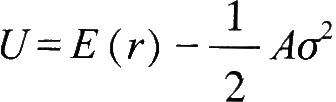
第3题：

第4题：

第5题：

答案：

解析：

第6题：

设李四仅消费X和y两种商品，他的效用函数为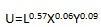

其中L为消费者闲暇小时数，假定李四的工资为每小时w，商品x和商品y的价格分别是

每周为7天，每天是24小时，劳动工资是其收入的全部来源，求当他每周最大化其效用时： (1)李四将选择每周工作多少小时？并将其收入多大比例用于购买x。 (2)李四消费z的需求价格弹性。 (3)如果李四的收入下降了30%，y的价格下降了50%，他将过得更好还是更坏？

答案：

解析：

第7题：

假设某人生产与消费粮食(F)和蔬菜(C)二在其一时期中，他决定工作200小时，至于把这些时间用到生产粮食上还是蔬菜上是无差异的，此人的粮食产量为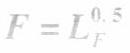

蔬菜产量为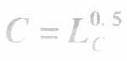

其中，LF与LC分别为花在生产粮食和蔬菜上的时间。此人的效用函数为U=(FC)^0.5. 试计算： (1)如果他无法与外部世界进行贸易，他将如何配置他的劳动时间以及他的粮食、蔬菜产量？为何？ (2)假设可以进行贸易且PF/PC=2/1，给定(1)中的产量，他将如何选择他的消费？

答案：

解析：

由题意可知求最大化问题，即：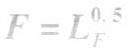

第8题：

设某人拥有的财富为w，其效用函数形式为u（w）=1/w，他面对如下一个彩票：以概率p得到w₁，以概率1-p得到w₂，他需要拥有多少财富w使得他接受这个彩票和保持现有财富是无差异的。

第9题：

将R1＞R2＞R3三只电阻串联，接在电压为U的电源上，获得最大功率的电阻是（）。

• A、R1；
• B、R2；
• C、R3；
• D、三个都一样；

第10题：

某消费者的效用函数为U＝lY＋l，其中，l为闲暇，Y为收入（他以固定的工资率出售其劳动所获得的收入）。求该消费者的劳动供给函数。他的劳动供给曲线是不是向上倾斜的？

第11题：

第12题：

第13题：

答案：B

解析：

投资者效用函数U＝E（r）－Aσ2是一个被许多金融理论者和CFA机构采用的投资组合的效用评分方法。式中，U表示效用值，A为投资者的风险厌恶系数。系数

只是一个约定俗成的分数项。上式实际包含了这样一种观点，即认为效用随着期望收益的增加和风险的减少而增长。

第14题：

答案：

解析：

关于凸集与非凸集，凸函数与凹函数，很多同学一直混淆，在此整理下相关定义和概念，希望给有需要的人。 凸集：集合中的任意两点连线的点都在该集合中，则称该集合为凸集；凹集为非凸集。 函数的凹凸是由函数“上方”集合的凹凸性决定的（注意是上方），该集合为凸集则该函数为凸函数，该集合为凹集则该函数为凹函数。如下图所示，图（A）代表凸集，图（B）则不是凸集。

第15题：

答案：

解析：

(3)间接效用函数衡量的是在收入和价格一定的情况下，消费者选择最优消费束时的效用。将(2)中所求的马歇尔需求函数代入原效用函数中，可得间接效用函数为：

支出函数是指在一组特定的商品价格条件下，要达到某一既定的效用水平所必需的最小支出，与 间接效用函数互为反函数，可得支出函数为：

第16题：

设张三仅消费x和y两种商品，他的效用函数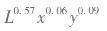

其中L是张三每周的闲暇小时数，试求他最大化其效用函数时： (1)他将选择每周工作多少小时？ (2)他将把收入的多大比例用于购买x？ (3)他消费x的需求价格弹性。 (4)如果他的收入下降30%，y的价格下降50%，他将过得更好还是更坏？

答案：

解析：

(1)假设张三的工资率为山，商品x和y的价格分别为Px和Py每周的总收入为( 24×7-L)ω=168ω -Lω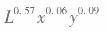

因此，张三每周工作的时间为168 -1=168 -133= 35（小时）。 (2)张三每周的总收入为（168 -1）ω=35ω 所以，张三用于x商品的支出比例为

(3)消费x的需求价格弹性为：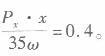

(4)原先消费者的效用为：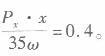

由(1)可知，收入和商品y价格的变化不会改变张三工作与休闲的时间。收入下降30%主要表现为工资率减少30%。 因此，当收入下降30%、y的价格下降50%时，张三的效用为：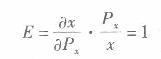

第17题：

答案：

解析：

第18题：

答案：C

解析：

第19题：

答案：A

解析：

第20题：

若某消费者的效用函数为U=XY⁴，他会把收入的多少用于商品Y上？

第21题：

中国城镇居民每天平均闲暇时间大概为（）小时。

• A、3
• B、4
• C、5
• D、7

第22题：

第23题：