在一个完全竞争的成本不变行业中,单个厂商的长期成本函数为LTC=Q3 - 40Q2+600Q,该市场的需求函数为Qd=13000 - 5P。求: (1)该行业的长期供给曲线。 (2)该行业实现长期均衡时的厂商数量。
题目
相似考题
更多“在一个完全竞争的成本不变行业中,单个厂商的长期成本函数为LTC=Q3 - 40Q2+600Q,该市场的需求函数为Qd=13000 - 5P。求: (1)该行业的长期供给曲线。 (2)该行业实现长期均衡时的厂商数量。”相关问题
-
第1题:
假设在完全竞争行业中有许多相同的厂商,代表性厂商LAC曲线的最低点的值为6美元,产量为500单位;当工厂产量为550单位的产品时,各厂商的SAC为7美元;还知市场需求函数与供给函数分别是:QD=80000-5000P、QS=35000+2500P(1)求市场均衡价格,并判断该行业是长期还是在短期处于均衡?为什么?(2)在长期均衡时,该行业有多少家厂商?(3)如果市场需求函数发生变动,变为Q′d=95000-5000P,试求行业和厂商的新的短期的均衡价格及产量,厂商在新的均衡点上,盈亏状况如何?
参考答案:(1)已知市场需求函数与供给函数分别为:QD=80000-5000P和QS=35000-2500P,市场均衡时QD=QS即80000-5000P=35000-2500P,所以市场均衡价格P=6(美元),这与代表性厂商LAC曲线最低点的值(6美元)相等。故该行业处于长期均衡状态。
(2)长期均衡价格P=6美元时,则长期均衡产量QS=QD=80000-5000×6=50000(单位)而长期均衡时每家厂商的产量为500单位,故该行业厂商人数为n=50000/500=100,即该行业有100有厂商。
(3)新的需求函数为Q′d=95000-5000P,但供给函数仍为QS=35000+2500P。新的市场均衡时Q′D=QS,即95000-5000P=35000+2500P,因而新的市场均衡价格P=8美元(也即行业短期均衡价格),行业短期均衡产量为:Q′d=QS=35000+2500×8=55000。在短期,厂商数不会变动,故仍是100家,因此,在新的均衡中,厂商产量Q/N=55000/100=550。从题中假设知道,当产量为550单位时,厂商的SAC为7美元。可见,在短期均衡中价格大于平均成本,厂商有盈利,利润为π=(P-SAC.Q=(8-7)×550=550(美元)
-
第2题:
已知完全竞争市场上单个厂商的长期成本函数为LTC=Q3-20Q2+200Q,市场的产品价格为P=600。 求:(1)该厂商实现利润最大化时的产量、平均成本和利润各是多少? (2)该行业是否处于长期均衡,为什么?(3)该行业处于长期均衡时每个厂商的产量、平均成本和利润各是多少? (4)判断(1)中的厂商是处于规模经济阶段,还是处于规模不经济阶段?
参考答案:(1)单个厂商总收益TR=PQ=600Q,
边际收益MR=TR’(Q)=600
单个厂商边际成本MC=3Q2-40Q+200
实现利润最大化的条件为MR=MC,
即600=3Q2-40Q+200,
解得Q=20或Q=-20/3(舍去)
此时对应的平均成本LAC=LTC/Q=Q2-20Q+200=20×20-20×20+200=200
利润=TR-TC=600×20-(203-20×202+200×20)=8000
(2)完全竞争行业处于长期均衡时利润为0,现在还有利润存在,因此没有实现长期均衡。
(3)行业处于长期均衡时价格为长期平均成本的最小值。
LAC=LTC/Q=Q2-20Q+200,LAC对Q求导为0时,LAC出现极值,
即LAC’(Q)=2Q-20=0,Q=10时候实现长期均衡,此时每个厂商的产量为10
平均成本LAC=102-20×10+200=100
利润=(P-LAC.*Q=(100-100)*10=0
(4)(1)中厂商的产量为20,高于长期均衡时的产量,因此,厂商处于规模不经济状态。
-
第3题:
完全竞争行业的代表厂商的长期总成本函数为:LTC=Q3-60Q2+1 500Q,成本用美元计算,Q为每月产量。
$(1)假设产品价格P=975美元,求利润为极大时的产量。
$(2)润为极大时的长期平均成本是多少?利润是多少?为什么这与行业的长期均衡相矛盾?
$(3)如该行业是成本固定不变行业,试推导出行业的长期供给函数。
正确答案:
[参考答案]
(1)该厂商的长期边际成本函数是
完全竞争行业中厂商利润极大时P=LMC,已知产品价格P=975美元,因此利润极大时975=3Q2-120q+1 500,得Q1=35,Q2=5。利润极大化还要求利润函数的二阶导数为负。

(2)当Q=35时,上述利润为极大时的长期平均成本 此时利润π=TR-IXC=P·Q-LAC·Q=12 250美元。
此时利润π=TR-IXC=P·Q-LAC·Q=12 250美元。
上面计算出来的结果与行业的长期均衡是相矛盾的,因为行业长期均衡要求留存于行业中的厂商只能获得正常利润,不能获得超额利润,而现在却存在超额利润π=12 250美元。之所以出现这一矛盾,是因为在完全竞争行业中,行业长期均衡时,价格应当是最低平均成本。在(1)中,我们已求得LAC=Q2-60Q+1 500,则对LAC求导,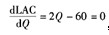 ,得Q=30。当Q=30时,求得最低平均成本LAC=600。因此,行业长期均衡时的价格应为600,而现在却为975,因而出现了超额利润。
,得Q=30。当Q=30时,求得最低平均成本LAC=600。因此,行业长期均衡时的价格应为600,而现在却为975,因而出现了超额利润。
(3)行业是成本固定不变行业,则该行业的长期供给曲线是一条水平线。从(2)已知,该行业的长期均衡价格为P=600,由此可得该行业的长期供给曲线为P=600。 -
第4题:
在某垄断竞争市场中,代表性厂商的长期成本函数为LTC =5Q3 -200Q2 +2700Q,市场的反需求函数为p= 2200A - 100Q,求:在长期均衡时,代表性厂商的产量和产品价格及A的数值。答案:解析:垄断竞争市场的长期均衡条件为M=LMC= SMC和AR= LAC= SAC。 由题意及上述条件可得:LMC =15Q2 -400Q+2700,LAC =5Q2—200Q +2700。 由市场的需求函数P= 2200A -100Q可得:MR= 2200A - 200Q,AR= 2200A -100Q。 联立上述方程可得:Q =10,P=1200,A=1。 -
第5题:
已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数为LTC= Q3 - 12Q2+40Q。试求: (1)当市场产品价格为P=100时,厂商实现MR= LMC时的产量、平均成本和利润。 (2)该行业长期均衡时的价格和单个厂商的产量。 (3)当市场的需求函数为Q=660 -15P时,行业长期均衡时的厂商数量。答案:解析:
故Q=6是长期平均成本最小化的解。 以Q=6代入LAC( Q),得平均成本的最小值为LAC =62 -12 x6+40 =4。 由于完全竞争行业长期均衡时的价格等于厂商的最小的长期平均成本,所以,该行业长期均衡时的价格P=4,单个厂商的产量Q=6。 (3)由于完全竞争的成本不变行业的长期供给曲线是一条水平线,而且相应的市场长期均衡价格是固定的,它等于单个厂商的最低的长期平均成本,所以,本题的市场长期均衡价格固定为P=4。以P=4代入市场需求函数Q=660 -15P,便可以得到市场的长期均衡数量为Q=660 -15 x4= 600。 现已求得在市场实现长期均衡时,市场的均衡数量Q =600,单个厂商的均衡产量Q=6。于是,行业长期均衡时的厂商数量= 600÷6=100。 -
第6题:
已知某完全竞争行业中的单个厂商的短期成本函数为STC =0.1Q3- 2Q2+150 +10 . (1)求当市场上产品的价格为P=55时,厂商的短期均衡产量和利润。 (2)当市场价格下降为多少时,厂商必须停产? (3)求厂商的短期供给函数。答案:解析:

-
第7题:
已知完全竞争市场上单个厂商的长期成本函数为LTC =Q3-20Q2+200Q,市场的产品价格为P= 600 . (1)该厂商实现利润最大化时的产量、平均成本和利润各是多少? (2)该行业是否处于长期均衡?为什么? (3)该行业处于长期均衡时每个厂商的产量、平均成本和利润各是多少? (4)判断(1)中的厂商是处于规模经济阶段,还是处于规模不经济阶段?答案:解析:

所以,当Q =10时,LAC曲线达到最小值。 以Q =10代入LAC函数,可得最小的长期平均成本=102 - 20 x10 +200 =100。 综合(1)和(2)的计算结果,我们可以判断(1)中的行业未实现长期均衡。因为由(2)可知,当该行业实现长期均衡时,市场的均衡价格应等于单个厂商的LAC曲线最低点的高度,即应该有长期均衡价格P =100,而且单个厂商的长期均衡产量应该是Q=10,还应该有每个厂商的利润π=O。而事实上由(1)可知,该厂商实现利润最大化时的价格P=600,产量Q=20,π=8000。显然,该厂商实现利润最大化时的价格、产量和利润都大于行业长期均衡时对单个厂商的要求,即价格600> 100,产量20 >10,利润8000 >0。因此,(1)中的行业未处于长期均衡状态。 (3)由(2)已知,当该行业处于长期均衡时,单个厂商的产量Q=10,价格等于最低的长期平均成本,即有P= LACmin=100,利润L=0。 (4)由以上分析可以判断,(1)中的厂商处于规模不经济阶段。其理由在于:(1)中单个厂商的产量Q =20,价格P=600,它们都分别大于行业长期均衡时单个厂商在LAC曲线最低点生产的产量Q =10和面对的价格P=100。换言之,(1)中的单个厂商利润最大化的产量和价格组合发生在LAC曲线最低点的右边,即LAC曲线处于上升段,所以,单个厂商处于规模不经济阶段。 -
第8题:
一个完全竞争行业中的一个典型厂商,其长期总成本函数为LTC =q3- 60q2+1500q,其中成本的单位为元,q为月产量. (1)推导出其长期平均成本和长期边际成本函数。 (2)若产品市场价格为975元,为实现利润最大化,厂商的产量将是多少? (3)厂商在(2)中的均衡是否与行业均衡并存? (4)若市场的需求曲线为P=9600 -Q,在长期均衡中,该行业将有多少厂商?答案:解析:
-
第9题:
假定在完全竞争行业中有许多相同的厂商,代表性厂商LAC曲线的最低点的值为6元,产量为500单位;当厂商产量为550单位的产品时,各厂商的SAC为7元;已知市场需求函数与供给函数分别是:QD=80000-5000P,QS=35000+2500P。在长期均衡时,该行业有多少厂商?
正确答案: 当处于均衡时:QD=QS
80000-50O0P=35000+2500P
求出:
QD=QS=50000
长期均衡时厂商的产量为500单位,所以该行业有50000/500=100家厂商。 -
第10题:
已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3—2Q2+15Q+10。试求:(1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润;(2)当市场价格下降为多少时,厂商必须停产;(3)厂商的短期供给函数。
正确答案: (1)P=MR=55
短期均衡时SMC=0.3Q2-4Q+15=MR=55
0.3Q2-4Q-40=0
∴Q=20或Q=-20/3(舍去)
利润=PQ-STC=55×20-(0.1×8000-2×400+15×20+10)=790
(2)厂商停产时,P=AVC最低点。
AVC=SVC/Q=(0.1Q3—2Q2+15Q)/Q=0.1Q2-2Q+15
AVC最低点时,AVC′=0.2Q-2=0
∴Q=10
此时AVC=P=0.1×100-2×10+15=5
(3)短期供给函数为P=MC=0.3Q2-4Q+15(取P>5一段) -
第11题:
问答题已知完全竞争市场的需求函数为D=6300-400P,短期市场供给函数为SS=3000+150P,单个企业在LAC曲线最低点的价格为6,产量为50,单个企业的成本规模不变。 求:(1)市场短期均衡价格与均衡产量。 (2)判断该市场是否同时处于长期均衡,求行业内的厂商数量。 (3)如果市场的需求函数变为D′=8000-400P,短期供给函数SS′=4700+150P,求市场短期均衡的价格和产量。 (4)判断该市场是否同时处于长期均衡,并求行业内厂商数量。正确答案: (1)由D=SS得:6300-400P=3000+150P,解得市场短期均衡价格与均衡产量分别为:P=6,Q=3900。
(2)P=6=LACmin,所以该市场处于长期均衡,行业内的厂商数量n=Q/50=78。
(3)由D′=SS′得:8000-400P=4700+150P,解得市场短期均衡价格与均衡产量分别为:P′=6,Q′=5600。
(4)P′=6=LACmin,所以该市场处于长期均衡,行业内的厂商数量n=Q′/50=5600/50=112。解析: 暂无解析 -
第12题:
问答题某竞争行业所有厂商的规模都相等,都是在产量达到500单位时达到长期平均成本的最低点4元,当用最优的企业规模生产600单位产量时,每一个企业的短期平均成本为4.5元,市场需求函数为Q=70000-5000P,供给函数为Q=40000+2500P,求解下列问题: (1)市场均衡价格是多少?该行业处于短期均衡还是长期均衡? (2)当处于长期均衡时,该行业有多少厂商? (3)如果市场需求变化为Q=100000-5000P,求行业与厂商新的短期均衡价格与产量,在新的均衡点,厂商盈利还是亏损?正确答案: (1)由均衡条件知:
70000-5000P=40000+2500P
解得:P=4,Q=50000。
由于均衡价格与长期平均成本的最低点相等,故该行业处于长期均衡。
(2)n=50000/500=100,所以当处于长期均衡时,该行业有100个厂商。
(3)由均衡条件知:
100000-5000P=40000+2500P
得均衡价格P=8,Q=60000。
每个厂商q=60000/100=600,此时厂商的短期平均成本为4.5元,所以厂商盈利(8>4.5)。解析: 暂无解析 -
第13题:
已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数LTC=Q3-12Q2+40Q。试求:(1)当市场商品价格是P=100,厂商实现MR=LMC时的产量,平均成本和利润;(2)该行业长期均衡时的价格和单个厂商的产量;(3)市场的需求函数为Q=660-15P时,行业长期均衡时的厂商数量。
参考答案:(1)LTC′=LMC=3Q2-24Q+40=MR=P=100
此时,3Q2-24Q+60=0,∴Q=10或Q=-2(舍去);LAC=Q2-12Q+40=20;利润=(P-LAC.Q=800
(2)LAC最低点=PLAC′=2Q-12=0,∴Q=6LAC最低点=4
即该行业长期均衡时的价格为4,单个厂商的产量为6
(3)成本不变行业长期均衡时价格是市场均衡价格,所以市场需求为Q=660-15×4=600,则厂商数量为600/6=100
-
第14题:
完全竞争企业的长期成本函数LTC = Q3-6Q2 + 30Q + 40,市场需求函数Qd=204-10P,P=66,试求:
(1)长期均衡的市场产量和利润
(2)这个行业长期均衡时的企业数量
参考答案:因为LTC = Q3 -6Q2 + 30Q + 40
所以MC=3Q2 -12Q+30
根据利润最大化原则MR=MC 得Q=6
利润=TR-TC=176
-
第15题:
已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3-2Q2+15Q+10
求:
(1)当市场价格下降为多少时,厂商必须停产?
(2)厂商的短期供给曲线
正确答案:(1) A价值增加为:5000-3000=2000万美元
B价值增加为:500-200=300万美元
C价值增加为:6000-2000=4000万美元
合计价值增加为:2000+300+4000=6300万美元
(2)最终产品价值为:2800+500+3000=6300万美元
(3)原来GDP为6300,现在加上进出口因素,GDP变为:6300+(1500-1000)=6800万美元。净出口额为:1500-1000=500万美元 -
第16题:
完全竞争市场中厂商长期成本函数为c(q)= 1000 +1Oq2(g>o),q=0,c=O.市场需求函数为p =1200 - 2q。 (1)求厂商长期供给函数。 (2)长期均衡时行业中有多少厂商? (3)求长期均衡时的消费者剩余。答案:解析:
-
第17题:
在一个完全竞争市场中,行业的生产成本不变,单个厂商的长期成本函数为LTC=Q3-4002+600Q。又假设该市场的需求函数为Q=13000-5P。问: (1)该行业的长期供给曲线是什么? (2)该行业实现长期均衡时的厂商数量是多少?答案:解析:
-
第18题:
已知某完全竞争的成本递增行业的长期供给函数LS= 5500 +300P。试求: (1)当市场需求函数为D=8000 - 200P时,市场的长期均衡价格和均衡产量。 (2)当市场需求增加时,市场需求函数为D=10000 - 200P时,市场长期均衡价格和均衡产量。 (3)比较(1)和(2),说明市场需求变动对成本递增行业的长期均衡价格和均衡产量的影响。答案:解析:(1)根据在完全竞争市场长期均衡时的条件LS =D,即有5500 +300P= 8000 - 200P,解得Pe =5。 把Pe=5代入LS函数,得Q。=5500 +300×5=7000。 所以,市场的长期均衡价格和均衡数量分别为Pe=5、Qe=7000。 (2)同理,根据LS =D,有5500+ 300P =10000 - 200P,解得Pe=9。 以Pe=9代人LS函数,得Qe=5500 +300×9=8200。 所以,市场的长期均衡价格和均衡数量分别为Pe=9、Qe=8200。 (3)比较(1)和(2)可得,对于完全竞争的成本递增行业而言,市场需求增加,会使市场的均衡价格上升,即由Pe=5上升为Pe=9,市场的均衡数量也增加,即由Qe=7000增加为Qe=8200。也就是说,市场需求与均衡价格成同方向的变动,与均衡数量也成同方向的变动。 -
第19题:
假设某完全竞争行业有200个相同的企业,企业的短期成本函数为TC =0. 2Q2+Q+15,市场需求函数为Qp= 2475 - 95P,厂商的长期总成本函数为LTC=0.1Q3-1. 2Q2+11.1Q,求: (1)市场短期均衡价格、产量及厂商利润。 (2)市场长期均衡价格与产量。 (3)说明是否会有厂商退出经营。答案:解析:(1)先求单个企业的供给函数: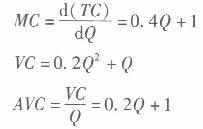
故A VC的最小值为1。 而MC的最小值也为1,故只有价格大于等于1,厂商才会供给商品。 此时单个企业的供给函数为P= MC =0.4Q +l,即Q=2.SP -2.5。 市场的供给函数为Qs=200Q =500P -500(P≥1),由QD=QS可得P=5。 市场均衡产量为2000单位,每个厂商产量为10单位。 单个厂商利润为5 x10 - (0.2 x102 +10+15) =5。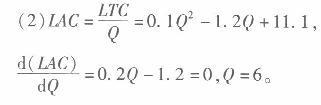
将Q=6代入LAC,得IAC =7.5。 由长期均衡条件可得P=7. 5. (3)将P=7.5代入需求函数可得市场需求量为1762.5,而200个厂商的供给量为1200,再加上厂商短期利润为正,长期利润为O,所以没有厂商退出经营。 -
第20题:
已知某完全竞争市场的需求函数为D= 6300 - 400P,短期市场供给函数为SS= 3000+150P;单个企业在LAC曲线最低点的价格为6,产量为50;单个企业的成本规模不变. (1)求市场的短期均衡价格和均衡产量。 (2)判断(1)中的市场是否同时处于长期均衡,求行业内的厂商数量: (3)如果市场的需求函数变为D’=8000 - 400P,短期供给函数为SS’= 4700 +150P,求市场的短期均衡价格和均衡产量。 (4)判断(3)中的市场是否同时处于长期均衡,并求行业内的厂商数量。 (5)判断该行业属于什么类型。 (6)需要新加入多少企业,才能提供由(1)到(3)所增加的行业总产量?答案:解析:(1)根据市场短期均衡的条件D=SS,有6300 - 400P= 3000 +150P,解得P=6。 以P=6代入市场需求函数,有Q=6300 - 400×6=3900。 所以,该市场短期均衡价格和均衡产量分别为P=6、Q=3900: (2)因为该市场短期均衡时的价格P=6,由题意可知,单个企业在LAC曲线最低点的价格也为6,所以,由此可以判断该市场也同时处于长期均衡。 由(1)可知市场长期均衡时的数量为Q=3900,由题意可知,在市场长期均衡时单个企业的产量为50,所以,由此可以求出市场长期均衡时行业内的厂商数量为3900÷50= 78。 (3)根据市场短期均衡的条件D’=SS’,有8000 - 400P’=4700 +150P’,解得P’=6。 以P’ =6代入市场需求函数,有Q’= 8000 - 400×6=5600。 或者以P’=6代人市场短期供给函数,有Q’=4700 +150×6=5600。 所以,该市场在变化了的供求函数条件下的短期均衡价格和均衡产量分别为P’=6、Q’=5600。 (4)与(2)的分析相类似,在市场需求函数和短期供给函数变化之后,该市场短期均衡时的价格P=6,由题意可知,单个企业在LAC曲线最低点的价格也是6,所以,由此可以判断该市场的这一短期均衡同时也是长期均衡。 因为由(3)可知,供求函数变化以后的市场长期均衡时的产量Q’=5600,由题意可知,在市场长期均衡时单个企业的产量为50,所以,由此可以求出市场长期均衡时行业内的厂商数量为5600÷50= 112。 (5)由以上分析和计算过程可知:在该市场供求函数发生变化前后的市场长期均衡时的均衡价格是不变的,均为P=6,而且单个企业在LAC曲线最低点的价格也是6。于是,我们可以判断该行业属于成本不变行业。以上(1)~(5)的分析与计算结果的部分内容如图6—6所示。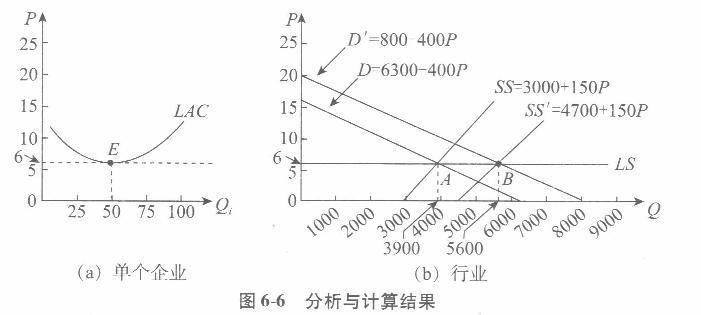
(6)由(1)和(2)可知,(1)时的厂商数量为78;由(3)和(4)可知,(3)时的厂商数量为112。因此,由(1)到(3)所增加的厂商数量为112 - 78= 34:或者,也可以这样计算:由于从(1)到(3)市场长期均衡产量的增加量为AQ= 5600 - 3900=1700。由题意可知,单个企业长期均衡时的产量为Q=50,所以,为提供AQ =1700的新增产量,需要新加入的企业数量为1700÷50= 34。 -
第21题:
假定在完全竞争行业中有许多相同的厂商,代表性厂商LAC曲线的最低点的值为6元,产量为500单位;当厂商产量为550单位的产品时,各厂商的SAC为7元;已知市场需求函数与供给函数分别是:QD=80000-5000P,QS=35000+2500P。市场均衡价格,并判断该行业是在长期还是在短期处于均衡?为什么?
正确答案:市场均衡时P=6与代表性企业厂商LAC曲线的最低点的值相等,故行业处于长期均衡状态。 -
第22题:
问答题已知完全竞争市场上单个厂商的长期成本函数为LTC=Q3-20Q2+200Q,市场的产品价格为P=600。 求:(1)该厂商实现利润最大化时的产量、平均成本和利润各是多少? (2)该行业是否处于长期均衡,为什么?(3)该行业处于长期均衡时每个厂商的产量、平均成本和利润各是多少? (4)判断(1)中的厂商是处于规模经济阶段,还是处于规模不经济阶段?正确答案: (1)单个厂商总收益TR=PQ=600Q,
边际收益MR=TR’(Q)=600
单个厂商边际成本MC=3Q2-40Q+200
实现利润最大化的条件为MR=MC,
即600=3Q2-40Q+200,
解得Q=20或Q=-20/3(舍去)
此时对应的平均成本LAC=LTC/Q=Q2-20Q+200=20×20-20×20+200=200
利润=TR-TC=600×20-(203-20×202+200×20)=8000
(2)完全竞争行业处于长期均衡时利润为0,现在还有利润存在,因此没有实现长期均衡。
(3)行业处于长期均衡时价格为长期平均成本的最小值。
LAC=LTC/Q=Q2-20Q+200,LAC对Q求导为0时,LAC出现极值,
即LAC’(Q)=2Q-20=0,Q=10时候实现长期均衡,此时每个厂商的产量为10
平均成本LAC=102-20×10+200=100
利润=(P-LAC.*Q=(100-100)*10=0
(4)(1)中厂商的产量为20,高于长期均衡时的产量,因此,厂商处于规模不经济状态。解析: 暂无解析 -
第23题:
问答题已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数LTC=Q3-12Q2+40Q。试求:(1)当市场商品价格是P=100,厂商实现MR=LMC时的产量,平均成本和利润;(2)该行业长期均衡时的价格和单个厂商的产量;(3)市场的需求函数为Q=660-15P时,行业长期均衡时的厂商数量。正确答案: (1)LTC′=LMC=3Q2-24Q+40=MR=P=100
此时,3Q2-24Q+60=0,∴Q=10或Q=-2(舍去);LAC=Q2-12Q+40=20;利润=(P-LAC.Q=800
(2)LAC最低点=PLAC′=2Q-12=0,∴Q=6LAC最低点=4
即该行业长期均衡时的价格为4,单个厂商的产量为6
(3)成本不变行业长期均衡时价格是市场均衡价格,所以市场需求为Q=660-15×4=600,则厂商数量为600/6=100解析: 暂无解析
