在新古典增长模型中,人均生产函数为y=资本折旧率为d=0.04,储蓄率为s-0.2,人口增长率为n=0. 03,技术进步率为g=0. 02。求:(1)经济处于稳态的人均产出和资本存量。(2)黄金律水平下的储蓄率。
题目
在新古典增长模型中,人均生产函数为y=
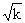
资本折旧率为d=0.04,储蓄率为s-0.2,人口增长率为n=0. 03,技术进步率为g=0. 02。求:(1)经济处于稳态的人均产出和资本存量。(2)黄金律水平下的储蓄率。
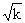
资本折旧率为d=0.04,储蓄率为s-0.2,人口增长率为n=0. 03,技术进步率为g=0. 02。求:(1)经济处于稳态的人均产出和资本存量。(2)黄金律水平下的储蓄率。
相似考题
更多“在新古典增长模型中,人均生产函数为y= ”相关问题
-
第1题:
在新古典增长模型中,总量生产函数为:
(1)求稳态时的人均资本量和人均产量。 (2)用这一模型解释“为什么我们如此富裕,而他们那么贫穷”。 (3)求出与黄金律相对应的储蓄率。答案:解析: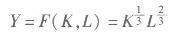
-
第2题:
假定总量生产函数为Y=(K)1/2(L)1/2。如果储蓄率为28%,人口增长率为1%,折旧率为6%。利用新古典增长模型,回答如下问题:(1)请计算稳态下的人均水平。(2)与黄金律水平相比,28%的储蓄率是过高,还是过低?(3)在向黄金律水平调整的过程中,人均消费、人均投资和人均产出的动态变化特征。答案:解析: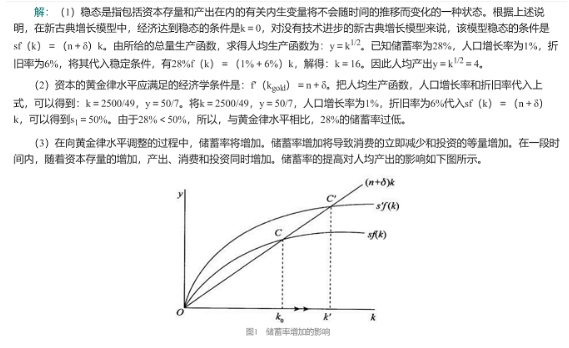
-
第3题:
设在新古典增长模型的框架下,生产函数为Y=F(K,L)=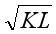
(1)求人均生产函数y=f(k)。 (2)若不存在技术进步,求稳态下的人均资本量、人均产量和人均消费量。答案:解析:
-
第4题:
在新古典增长模型中,已知生产函数为y=2k -0. 5k2,y为人均产出,k为人均资本,储蓄率s =0.1。人口增长率n=0.05,资本折旧率δ=0.05。试求: (1)稳态时人均资本和人均产量。 (2)稳态时人均储蓄和人均消费。答案:解析:
-
第5题:
已知新古典增长模型中人均生产函数为y=f(k) =2k-0. 5k2,最为人均资本,储蓄率s为0.4,人口增长率以为0.2%。 请计算: (1)经漭达到稳定状态的值。 (2)黄金律所要求的人均资本k值答案:解析:(1)经济达到稳态时,有k=sy-nk=0,解得k=3.99,即经济达到稳态时的人均资本存量为3. 99,人均产出为0.02。 (2)达到资本黄金律水平时,有MPK =n,解得k=1. 998,所以黄金律水平下的人均资本存量k=l. 998。 -
第6题:
△Y/Y=S/K,其说明一个国家国民生产总值增长率(△Y/Y)与其储蓄率S成正比,与其资本-产出比V成反比。这就是经济增长理论中著名的()的简单形式。
- A、刘易斯的两部门模型
- B、哈罗德-多马模型
- C、索洛的新古典增长模型
- D、新殖民主义依附模型
正确答案:B -
第7题:
在新古典增长模型中,均衡点是指人口的增长率为零。
正确答案:错误 -
第8题:
在新古典增长模型中,人均产出唯一地取决于人均资本量。
正确答案:正确 -
第9题:
在新古典增长模型中,人均产出增长是由于()。
- A、技术进步
- B、高储蓄率
- C、高人口增长率
- D、以上说法都正确
正确答案:A -
第10题:
在新古典经济增长模型中,经济稳定增长的条件是什么?
正确答案:新古典经济增长模型中,经济稳定增长的条件是人均资本不发生变化,或者说每人使用的资本量不变,这就要使人均储蓄正好等于资本的广化。在新古典经济增长模型公式sf(k)=k+nk中,人均资本不发生变化,就是k=0,sf(k)=nk,sf(k)是储蓄率和人均产量(收入)的乘积,即人均储蓄,nk是资本的广化。 -
第11题:
判断题在新古典增长模型中,人均产出唯一地取决于人均资本量。A对
B错
正确答案: 对解析: 暂无解析 -
第12题:
单选题在新古典增长模型中()。A人均产出是常数
B人均产出取决于人均资本量
C人均产出总是递增
D人均产出总是递减
正确答案: A解析: 暂无解析 -
第13题:
假设一个经济的人均生产函数为y=k,其中k为人均资本:求: (1)经济的总量生产函数。 (2)在没有人口增长和技术进步的情况下,假定年折旧率为δ=10%,储蓄率为s=40%。那么稳态下的人均资本、人均产出和人均消费分别为多少?答案:解析:
稳态人均消费为c=(1-s)y=0.6 x4 =2.4. -
第14题:
在索罗增长模型( Solow model)中,假设生产函数为柯布一道格拉靳函数Y=KaL1-a,已知n、g、б 、a。 (1)写出生产函数的简约形式y=f(k),其中y为人均产出,是为人均资本存量。 (2)已知s值,求解稳定状态下的y*、k*、c*。 (3)当s值未知时,求解黄金规则水平下的稳态y*、k*、s*、c*。答案:解析:
-
第15题:
在新古典增长模型中,人均生产函数为y=f(k) =2k -0.5k2,人均储蓄率为0.3,人口增长率为0.03.求: (1)使经济均衡增长的k值。 (2)与黄金律相对应的人均资本量。答案:解析:(1)新古典增长模型中,经济均衡增长时有sf (k)=nk,代人数值得0.3(2k -0.5k2)=0. 03k,有k=3.8。 (2)由题意,有f(k)=n,于是2-k=0.03,k=1.97,即为与黄金律相对应的稳态的人均资本量。 -
第16题:
在新古典增长模型中,人口增长对经济有哪些影响?答案:解析:新古典增长模型假定:①全社会只生产一种产品;②生产要素之间可以相互替代;③生产的规模收益不变;④储蓄率不变;⑤不存在技术进步和资本折旧;⑥人口增长率不变。新古典增长理论虽然假定劳动力按一个不变的比率n增长,但当把n作为参数时,就可以说明人口增长对产量增长的影响。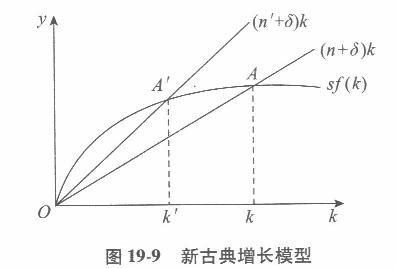
图19-9中,经济最初位于A点的稳态均衡。现在假定人口增长率从n增加到n’,则图19—9中的(n+8)k线便移动到(n’+δ)k线,这时,新的稳态均衡为A’点。比较A’点与A点可知,人口增长率的增加降低了人均资本的稳态水平(从原来的k减少到k’),进而降低了人均产量的稳态水平。西方学者进一步指出,作为人口增长率上升产生的人均产量下降正是许多发展中国家面临的问题。两个有着相同储蓄率的国家仅仅由于其中一个国家比另一个国家的人口增长率高,就可以有非常不同的人均收入水平。 对人口增长进行比较静态分析的另一个重要结论是,人口增长率的上升增加了总产量的稳态增长率。理解这一结论的要点在于懂得稳态的真正含义,并且注意到A’点和A点都是稳态均衡点。另外,由于A点和A’点都是稳态,故人口增加对人均资本和人均产量的增长率都不产生影响。 -
第17题:
在新古典增长模型中,生产函数为y=f(k)=2k-0. 5k2,人均储蓄率为s-0.3,设人口增长率为3%,求:(1)使经济均衡增长的k值。(2)黄金律所要求的人均资本量。答案:解析:(1)生产函数为y= f(k)一2k -0. 5k2,人均储蓄率为0.3,人口增长率为n=3%。当经济达到稳态时有:△k=s厂(k)-nk=0.3×(2k-0. Sk2)-0. 03k-0解得稳态时的人均资本水平: k-3.8 (2)当经济达到资本黄金律水平时有MPK=n,即有:2-k=3%解得黄金律所要求的人均资本存量为:K*gold=1. 97 -
第18题:
新古典增长模型可表示为?
正确答案: Δk=s·y-(n+δ)·k,即资本深化=人均储蓄(投资)—资本广化。 -
第19题:
在新古典增长模型中()。
- A、人均产出是常数
- B、人均产出取决于人均资本量
- C、人均产出总是递增
- D、人均产出总是递减
正确答案:B -
第20题:
在新古典增长模型中,资本-产出比率是常数。
正确答案:错误 -
第21题:
在新古典增长模型中,人均生产函数为y=f(k)=2k-0.5k*k,人均储蓄率为0.3,设人口增长率为3%。试求经济增长的k值。
正确答案:均衡时有sf(k)=nk,
即0.3*(2k-0.5k^2)=0.03k,
解得k=3.8 -
第22题:
问答题在新古典增长模型中,人均生产函数为y=f(k)=2k-0.5k*k,人均储蓄率为0.3,设人口增长率为3%。试求经济增长的k值。正确答案: 均衡时有sf(k)=nk,
即0.3*(2k-0.5k^2)=0.03k,
解得k=3.8解析: 暂无解析 -
第23题:
问答题在新古典增长模型中,集约化生产函数为Y=f(k)=2k-0.5k2,人均储蓄率为0.3,设人口增长率为3%,求:(1)使经济均衡增长的k值;(2)黄金分割律所要求的人均资本量。正确答案:
(1)经济均衡增长时,有sf(k)= nk,将s=0.3,n=3%代入,可得:
0.3(2k-0.5k2)=0.03k
化简得:20k-5k2=k,解得:k=3.8。
(2)按黄金分割律要求,对每个人的资本量的选择应使得资本的边际产品等于劳动的增长率,即f′(k)=n。
于是有2-k=0.03,解得k=1.97,即为与黄金率相对应的稳态的人均资本量。解析: 暂无解析
