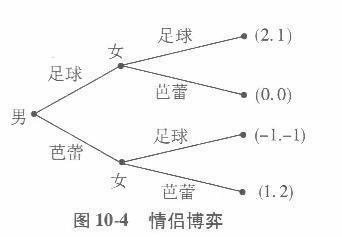
在下面的情侣博弈中(如图10-4所示),如果将第二个支付向量(0,O)改为(O,1.5),纳什均衡和逆向归纳策略会有什么变化?改为(0,1) 呢?
题目
在下面的情侣博弈中(如图10-4所示),如果将第二个支付向量(0,O)改为(O,1.5),纳什均衡和逆向归纳策略会有什么变化?改为(0,1) 呢?

相似考题
更多“在下面的情侣博弈中(如图10-4所示),如果将第二个支付向量(0,O)改为(O,1.5),纳什均衡和逆向归纳策略会有什么变化?改为(0,1) 呢? ”相关问题
-
第1题:
在动态博弈中,纳什均衡与逆向归纳策略有什么不同。答案:解析:完全信息动态博弈是指参与者选择策略有时间先后的博弈形式。序贯博弈中可能会存在多个纳什均衡,而逆向归纳法从众多的纳什均衡中进一步确定“更好的”纳什均衡。 -
第2题:
两个寡头厂商在进行博弈竞争,他们的策略及支付矩阵如下,则( )。 A.甲厂商有占优策略
A.甲厂商有占优策略
B.乙厂商没有占优策略
C.(中,中)是纳什均衡
D.没有纳什均衡答案:C解析:根据上述支付矩阵,不论甲选择“上”、“中”、“下”,对于乙来说选择“中”是占优策略;如果乙选择“左”,则甲会选择“下”;如果乙选择“中”,则甲会选择“中”;如果乙选择“右”,则甲会选择“中”。所以,对于甲、乙来说,(中,中)是一组纳什均衡。 -
第3题:
设某个纯策略博弈的纳什均衡不存在试问:相应的混合策略博弈的纳什均衡会存在吗?试举一例说明.答案:解析:在同时博弈中,纯策略的纳什均衡可能存在,也可能不存在,但相应的}昆合策略纳什均衡总是存在的。例如表10-9所示,在下面的二人同时博弈中,根据条件策略下划线法可知由于没有一个单元格中两个数字之下均有下划线,故纯策略的纳什均衡不存在,但是相应的混合策略纳什均衡却是存在的。
首先分别计算甲厂商和乙厂商的混合策略: E甲=4P1ql+9P1(1-ql)+7(1-P1)ql+2(1-P1)(1-q1) =p1(7 -1Oql) +5q1 +2 E乙= 6P1ql+P1(1- q1)+3(1-p1)ql+8(1- P1)(1- q1) =5q1(2p1 -1) -7P1+8 其次分别计算甲厂商和乙厂商的条件混合策略: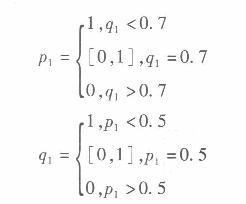
最后,混合策略纳什均衡参见图10-1中点e,此时混合策略纳什均衡可以表示为: ((P1,p2)(q1,q2))=((0.5,0.5)(0.7,0.3)) 但不存在纯策略博弈的纳什均衡。
-
第4题:
根据图10-7的博弈树模型,求: (1)纳什均衡。 (2)逆向归纳策略。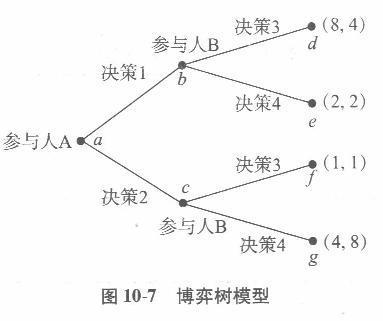 答案:解析:(1)如表10-13所示。
答案:解析:(1)如表10-13所示。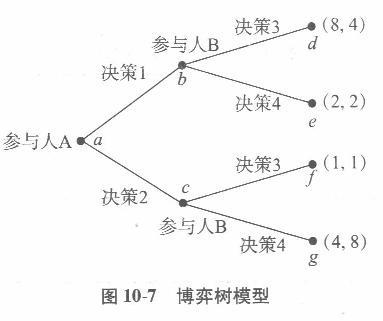
纯策略纳什均衡为(8,4)(4,8)即(决策l,决策3),(决策2,决策4)。 (2)逆向归纳策略纳什均衡为(8,4),即(决策1,决策3)。 -
第5题:
根据图10.8的博弈树模型,求 (1)纳什均衡。 (2)逆向归纳策略。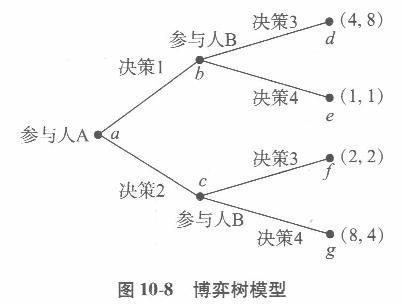 答案:解析:(1)如表10 -14所示。
答案:解析:(1)如表10 -14所示。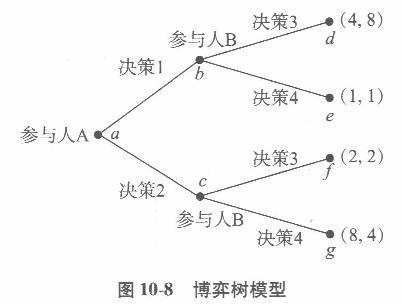
纳什均衡为(4,8)(8,4),即(决策1,决策3),(决策2,决策4)。 (2)逆向归纳策略纳什均衡为(决策2,决策4)。 -
第6题:
在一个博弈中如果存在多个纳什均衡则不存在上策均衡。
正确答案:正确 -
第7题:
不存在纯战略纳什均衡和存在惟一的纯战略纳什均衡,作为原博弈构成的有限次重复博弈,共同特点是重复博弈本质上不过是原博弈的简单重复,重复博弈的子博弈完美纳什均衡就是每次重复采用原博弈的纳什均衡。
正确答案:正确 -
第8题:
有关子博弈精炼纳什均衡说法错误的是().
- A、要求某一策略组合在每一个子博弈上都构成一个纳什均衡
- B、也是一个一般意义上的纳什均衡
- C、和纳什均衡没有关系
- D、要求某一策略组合在原博弈上都构成一个纳什均衡
正确答案:C -
第9题:
完全信息静态博弈对应以下哪项均衡?()
- A、纳什均衡
- B、子博弈精炼纳什均衡
- C、贝叶斯纳什均衡
- D、精炼贝叶斯纳什均衡
正确答案:A -
第10题:
关于纳什均衡的说法中,如下正确的是()
- A、在某些博弈中,可能就根本不存在纯策略的纳什均衡
- B、纳什均衡可能是有效率的也有可能是无效率的
- C、根据纳什均衡的定义,纳什均衡都是有效率的
- D、纳什均衡不可能存在着多重均衡
正确答案:A,B -
第11题:
混合策略纳什均衡与纯策略纳什均衡有什么不同?
正确答案:在纯策略博弈中,纳什均衡是参与人的一种策略组合,在该策略组合上,任何参与人单独改变其策略都不会得到好处;在混合策略博弈中,纳什均衡是参与人的一种概率向量组合,在该概率向量组合上,任何参与人单独改变其概率向量都不会得到好处。 -
第12题:
单选题完全信息静态博弈对应以下哪项均衡?()A纳什均衡
B子博弈精炼纳什均衡
C贝叶斯纳什均衡
D精炼贝叶斯纳什均衡
正确答案: B解析: 暂无解析 -
第13题:
试说明如果一个策略组合为博弈中唯一的纳什均衡,则该策略组合不会在重复剔除严劣策略的过程中被剔除。答案:解析:如果存在这样一个策略组合——给定该策略组合中其他参与者的选择,没有人有积极性改变自己的选择,就说该策略组合是一个纳什均衡。如表1-1所示
,在该博弈中,策略组合(不合作,不合作)是一个纳什均衡,且是唯一的纳什均衡。重复剔除严劣策略是指各参与人在其各自策略集中,不断剔除严劣策略,直到每个参与者都仅剩下一个策略为止,最后得到的策略组合就被称为重复剔除严劣策略均衡。 表1-1中,甲厂商策略“合作”严格劣于策略“不合作”,将其从参与者甲厂商的策略空间中剔除,得到表1-2
重复进行上述方法,得到最终解(不合作,不合作)。从分析中可以得出纳什均衡与重复剔除严劣策略均衡之间的关系:第一,纳什均衡不会被重复剔除严劣策略过程所剔除;第二,如果重复剔除严劣策略过程最终只剩下唯一的策略组合,那么这一策略组合为该博弈唯一的纳什均衡。 -
第14题:
在下面简化的博弈树模型中(如图10-2所示),确定纳什均衡和逆向归纳策略、 答案:解析:纳什均衡为(决策1,决策3)。 逆向归纳策略为:首先参与人曰删除决策4的终点和支付组合,然后参与人A删除决策2的终点和支付组合,从而逆向归纳策略为(决策1,决策3)。
答案:解析:纳什均衡为(决策1,决策3)。 逆向归纳策略为:首先参与人曰删除决策4的终点和支付组合,然后参与人A删除决策2的终点和支付组合,从而逆向归纳策略为(决策1,决策3)。 -
第15题:
设某个纯策略博弈的纳什均衡是有限的一试问:相应的混合策略博弈的纳什均衡会是无限的吗?试举一例说明:答案:解析:会存在,如表10-8所示。
-
第16题:
用逆向归纳法确定下面的“蜈蚣博弈”的结果(如图10-3所示):在该博弈中,第1步是A决策:如果A决定结束博弈,则A得到支付1,B得到支付O,如果A决定继续博弈,则博弈进入到第2步,由B作决策.此时,如果B决定结束博弈,则A得到支付0,B得到支付2,如果B决定继续博弈,则博弈进入到第3步,又由,A作决策,依次类推直到最后,博弈进入到第9999步,由A作决策此时,如果A决定结束博弈,则,A得到支付9999,B得到支付0;如果A决定继续博弈,则A得到支付O,B得到支付10000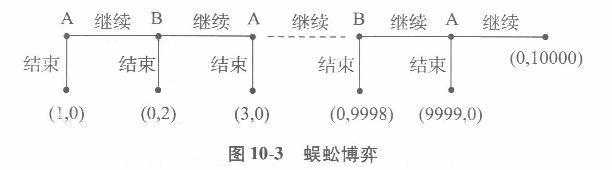 答案:解析:利用逆向归纳法,最后一步终点处,A选择结束,从而B选择结束,依次类推,在第一步4选择结束。
答案:解析:利用逆向归纳法,最后一步终点处,A选择结束,从而B选择结束,依次类推,在第一步4选择结束。 -
第17题:
斯塔克尔伯格模型中有关特征叙述错误的是().
- A、存在先行的主导企业和追随企业主导企业的产量决策是将追随企业的反应函数纳入自己的目标函数
- B、不可以采用逆向归纳法求解博弈的子博弈精炼纳什均衡
- C、由一阶条件这就是子博弈精炼纳什均衡结果D.
正确答案:C -
第18题:
子博弈精炼纳什均衡()。
- A、是一个一般意义上的纳什均衡;
- B、和纳什均衡没有什么关系;
- C、要求某一策略组合在每一个子博弈上都构成一个纳什均衡;
- D、要求某一策略组合在原博弈上都构成一个纳什均衡。
正确答案:C -
第19题:
多个纯战略纳什均衡博弈的有限次重复博弈子博弈完美纳什均衡路径:两阶段都采用原博弈同一个纯战略纳什均衡,或者轮流采用不同纯战略纳什均衡,或者两次都采用混合战略纳什均衡,或者混合战略和纯战略轮流采用。
正确答案:正确 -
第20题:
猎鹿博弈中存在三个纯策略的纳什均衡。
正确答案:错误 -
第21题:
在序贯博弈中,纳什均衡与逆向归纳策略有什么不同?
正确答案:与同时博弈一样,在序贯博弈中,纳什均衡也是指这样一些策略组合,在这些策略组合中,没有哪一个参与人会单独改变自己的策略。同样,在序贯博弈中,纳什均衡也可能不止一个。在这种情况下,可以通过逆向归纳法对纳什均衡进行“精炼”,即从多个纳什均衡中,排除掉那些不合理的纳什均衡,或者,从众多的纳什均衡中进一步确定“更好”的纳什均衡。经由逆向归纳法的精炼而得到的纳什均衡就是所谓的逆向归纳策略。 -
第22题:
在博弈论中,占优策略均衡总是纳什均衡吗?纳什均衡一定是占优策略均衡吗?
正确答案:占优策略均衡总是纳什均衡,而纳什均衡不一定是占优策略均衡。占有策略均衡是指博弈中所有参与者都不改变自己策略的一种状态。由博弈中所以参与者的占优策略(无论其他参与者采取什么策略,参与者的唯一最优策略就是他的占优策略)所组成的均衡就是占优策略均衡,而给其他参与者策略条件下每个参与者所选择的最优策略所构成的策略组合则是纳什均衡。显然占优策略均衡是纳什均衡的一种特殊情况。在这种情况下,不管其他参与者采取何种策略,本参与者所采取的策略总是要优于别的策略。而在纳什均衡中,只要对手策略给定的情况下,本策略者的策略最优即可。 -
第23题:
设某个纯策略博弈的纳什均衡是有限的。试问:相应的混合策略博弈的纳什均衡会是无限的吗?试举一例说明。
正确答案:当纯策略博弈的纳什均衡为有限时,相应的混合策略博弈的纳什均衡既可能是有限的,也可能是无限的。例如,在只包括A与B的二人同时博弈中,混合策略纳什均衡的“集合”可以是单位平面、三条线段、两条线段、一条线段、三个点、两个点和一个点,其中,前四种情况就意味着存在无限多个纳什均衡。
