美国的波音公司与法国的空客公司都向世界出售民用客机。假设世界对飞机的需求函数为p=20-q,两个公司的成本函数均为c(q)=8q。 假定两公司都生产,找出古诺/纳什均衡并求出均衡时的产量、价格与利润。
题目
美国的波音公司与法国的空客公司都向世界出售民用客机。假设世界对飞机的需求函数为p=20-q,两个公司的成本函数均为c(q)=8q。 假定两公司都生产,找出古诺/纳什均衡并求出均衡时的产量、价格与利润。
相似考题
更多“美国的波音公司与法国的空客公司都向世界出售民用客机。假设世界对飞机的需求函数为p=20-q,两个公司的成本函数均为c(q)=8q。 假定两公司都生产,找出古诺/纳什均衡并求出均衡时的产量、价格与利润。”相关问题
-
第1题:
假定某完全竞争行业有100个相同的厂商,单个厂商的短期总成本函数为.STC=Q2+6Q +20。 (l)求市场的短期供给函数。 (2)假定市场的需求函数为Qd=420 - 30P,求该市场的短期均衡价格和均衡产量。 (3)假定政府对每一单位商品征收1.6元的销售税,那么,该市场的短期均衡价格和均衡产量是多少?消费者和厂商各自负担多少税收?答案:解析:(1)单个厂商的边际成本MC =2Q +6。 由短期均衡条件可知P= MC,即P=2Q +6, 即Q =0.5P-3。 故市场的短期供给函数为Qs=100Q= 50P - 300。 (2)联立供给函数与需求函数,可得P=9,Q=150。 (3)征税后,联立函数:
解得Pd=10,Q=120。 故市场短期均衡价格为10,均衡产量为120。 消费者承担1元税收,厂商承受0.6元税收。 -
第2题:
某国电信市场原本由一家公司经营,其成本函数为TC=Q2- 10Q +30,市场需求为Qd=15 -P (1)求市场均衡产量、均衡价格及利润。 (2)现将该公司拆分为A、B两家公司,由于技术水平和规模状态的不同,A、B两家公司的成本,函数分别为
(A)假设两家公司独立行动,各自谋求本公司利润最大化,求均衡时A、B两家公司的产量、利润和市场价格。 (B)若两家公司共谋形成卡特尔,求均衡时A、日两家公司的产量、利润和市场价格。答案:解析:
-
第3题:
假设某大宗商品的国际需求函数Q=a-P。两个寡头公司1和2向该市场提供同质产品,拥有不变的单位边际成本,分别为c1和c2,且有a>c2 >c1。 若两个公司展开古诺(Cournot)竞争,则各自的纳什均衡产量q1和q2是多少?答案:解析:若两个企业展开古诺竞争,则寡头公司1的利润函数为: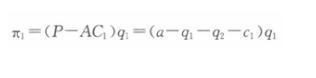
利润最大化的一阶条件为: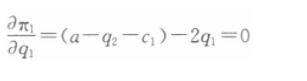
从而寡头公司1的反应函数为: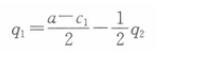
寡头公司2的利润函数为: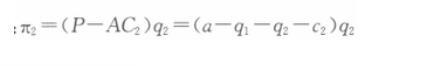
同理可得其反应函数为: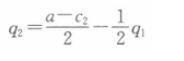
联立两个公司的反应函数①②可得: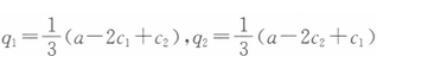
此即为古诺竞争 下的纳什均衡产量。 -
第4题:
已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数为LTC= Q3 - 12Q2+40Q。试求: (1)当市场产品价格为P=100时,厂商实现MR= LMC时的产量、平均成本和利润。 (2)该行业长期均衡时的价格和单个厂商的产量。 (3)当市场的需求函数为Q=660 -15P时,行业长期均衡时的厂商数量。答案:解析:
故Q=6是长期平均成本最小化的解。 以Q=6代入LAC( Q),得平均成本的最小值为LAC =62 -12 x6+40 =4。 由于完全竞争行业长期均衡时的价格等于厂商的最小的长期平均成本,所以,该行业长期均衡时的价格P=4,单个厂商的产量Q=6。 (3)由于完全竞争的成本不变行业的长期供给曲线是一条水平线,而且相应的市场长期均衡价格是固定的,它等于单个厂商的最低的长期平均成本,所以,本题的市场长期均衡价格固定为P=4。以P=4代入市场需求函数Q=660 -15P,便可以得到市场的长期均衡数量为Q=660 -15 x4= 600。 现已求得在市场实现长期均衡时,市场的均衡数量Q =600,单个厂商的均衡产量Q=6。于是,行业长期均衡时的厂商数量= 600÷6=100。 -
第5题:
美国的波音公司与法国的空客公司都向世界出售民用客机。假设世界对飞机的需求函数为p=20-q,两个公司的成本函数均为c(q)=8q。假定美国政府决定给予波音公司每架飞机3单位的生产补贴,问新的古诺/纳什均衡(价格、产量与各自利润)为多少?答案:解析:美国政府给予波音公司补助后,波音公司的成本函数变为c’1(q1)=8q1-3q1=5q1,波音公司 的利润函数变为:
利润最大化的一阶条件为:
得波音公司的反应函数为
同理可得空客公司的反应函数为
令q1=qe1,q2一qe2,联立两个反应函数,得到古诺均衡解为:q1 =6,q2 =3;p=11;π1=36,π2 =9。 -
第6题:
已知某完全竞争的成本递增行业的长期供给函数LS= 5500 +300P。试求: (1)当市场需求函数为D=8000 - 200P时,市场的长期均衡价格和均衡产量。 (2)当市场需求增加时,市场需求函数为D=10000 - 200P时,市场长期均衡价格和均衡产量。 (3)比较(1)和(2),说明市场需求变动对成本递增行业的长期均衡价格和均衡产量的影响。答案:解析:(1)根据在完全竞争市场长期均衡时的条件LS =D,即有5500 +300P= 8000 - 200P,解得Pe =5。 把Pe=5代入LS函数,得Q。=5500 +300×5=7000。 所以,市场的长期均衡价格和均衡数量分别为Pe=5、Qe=7000。 (2)同理,根据LS =D,有5500+ 300P =10000 - 200P,解得Pe=9。 以Pe=9代人LS函数,得Qe=5500 +300×9=8200。 所以,市场的长期均衡价格和均衡数量分别为Pe=9、Qe=8200。 (3)比较(1)和(2)可得,对于完全竞争的成本递增行业而言,市场需求增加,会使市场的均衡价格上升,即由Pe=5上升为Pe=9,市场的均衡数量也增加,即由Qe=7000增加为Qe=8200。也就是说,市场需求与均衡价格成同方向的变动,与均衡数量也成同方向的变动。 -
第7题:
假设某完全竞争行业有200个相同的企业,企业的短期成本函数为TC =0. 2Q2+Q+15,市场需求函数为Qp= 2475 - 95P,厂商的长期总成本函数为LTC=0.1Q3-1. 2Q2+11.1Q,求: (1)市场短期均衡价格、产量及厂商利润。 (2)市场长期均衡价格与产量。 (3)说明是否会有厂商退出经营。答案:解析:(1)先求单个企业的供给函数: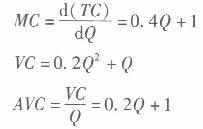
故A VC的最小值为1。 而MC的最小值也为1,故只有价格大于等于1,厂商才会供给商品。 此时单个企业的供给函数为P= MC =0.4Q +l,即Q=2.SP -2.5。 市场的供给函数为Qs=200Q =500P -500(P≥1),由QD=QS可得P=5。 市场均衡产量为2000单位,每个厂商产量为10单位。 单个厂商利润为5 x10 - (0.2 x102 +10+15) =5。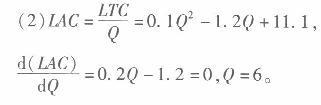
将Q=6代入LAC,得IAC =7.5。 由长期均衡条件可得P=7. 5. (3)将P=7.5代入需求函数可得市场需求量为1762.5,而200个厂商的供给量为1200,再加上厂商短期利润为正,长期利润为O,所以没有厂商退出经营。 -
第8题:
市场反需求函数为P=a-bQ,有N(N≥3)个同质企业,典型企业i的成本函数为TC(qi)=Qqi,其中Q为市场的总产量,且Q=(q1+q2…+qx)。 假设价格为P,求N个企业进行古诺竞争时每个企业的产量和利润,以及市场总产量和总利润。答案:解析:
-
第9题:
一个市场的需求函数为:P(Q)=100-2Q,企业的成本函数为:C(Q)=4Q,下列说法正确的有()。
Ⅰ.若该市场为完全竞争市场,则均衡价格P=4,均衡产量为48
Ⅱ.当市场上有2个企业时,若处于古诺均衡,则均衡价格是36
Ⅲ.当市场上有2个企业时,若处于斯塔克尔伯格均衡,则均衡价格为36
Ⅳ.当市场上有2个企业时,若达成卡特尔均衡,则两个企业都没有违约动机A.Ⅰ、Ⅱ
B.Ⅰ、Ⅲ
C.Ⅲ、Ⅳ
D.Ⅰ、Ⅱ、Ⅳ答案:A解析:工项.若市场为完全竞争市场.根据C(Q)=4Q可得,MC=AVC=4,则均

-
第10题:
下列有关古诺纳什均衡说法错误的是().
- A、模型中两个反应函数的交叉点就是纳什均衡
- B、双方所做的产量决策都为给定对方所做的产量决策的前提下的最优决策,因而双方都没有动力改变其产量
- C、当价格等于边际成本时,便达到古诺均衡各厂商的利润为零
- D、古诺纳什均衡具有稳定性,如果企业没有在古诺均衡点进行生产,它们会自动调整产量直到
正确答案:C -
第11题:
问答题假设某垄断竞争厂商的产品需求函数为P=9400-4Q,成本函数为TC=4000+3000Q,求该厂商均衡时的产量、价格和利润。正确答案: 根据利润最大化原则MR=MC,MR=9400-8Q,MC=3000,得Q=800,P=6200,π=TR-TC=2556000解析: 暂无解析 -
第12题:
问答题假设垄断企业的成本函数为50+20Q,其面对的市场需求函数为P=100-4Q,试求垄断企业利润最大化的产量、价格与利润。正确答案:
垄断企业其面对的市场需求函数为P=100—4Q,边际收益为:MR=100-8Q;
边际成本为:MC=20;
由MR=MC可以解得:Q=10;
价格为:P=100-4Q=60;
利润为:10×60-50-20×10=350。解析: 暂无解析 -
第13题:
假设在一个市场上有两家企业,该市场的逆需求函数为P=4一罢,企业1的成本函数为 c1= q1,企业2的成本函数为C2 =2q2,P为价格,Q为两个企业的总产量,q为每个企业的产量。 (1)假设两个企业可以组成一个卡特尔,求垄断价格及每个企业的产量。 (2)试证明:卡特尔不是一个纳什均衡。 (3)假设两个企业进行产量竞争,求古诺均衡下的价格和每个企业的产量。答案:解析:(1)由已知可得企业1和企业2的边际成本分别为:MCl =1,MC2=2。因为MC2> MC1,所以,为使卡特尔总利润最大化,应当使企业1生产,企业2不生产。因此,Q—qi,q2 =0。 卡特尔的利润函数为: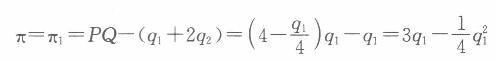
利润最大化的一阶条件为: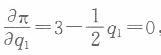
解得:q1=6。 将q1=6和q2=O代入需求函数,可得P=5/2 (2)企业1的成本函数为c1=q1,企业2的成本函数为C2=2q2,可知卡特尔定价下P>MC2> Mc1,两个企业都有降低价格获得最大利润的冲动。因此,卡特尔不是一个纳什均衡。 (3)若两厂商进行古诺竞争,则寡头企业1的利润函数为: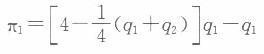
其利润最大化的一阶条件为: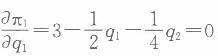
得企业1的反应函数为: q1=6-0. 5q2 ① 同理可得企业2的反应函数为: q2 =4-0. 5q1 ② 联立两个寡头厂商的反应函数①②可得:q.=16/3,q2 =4/3。从而得: P= 7/3,π1=64/9,π2=4/9 -
第14题:
市场上有两家企业E和D生产灯泡,市场需求函数Q=100-P。两家企业的成本函数Ci=10qi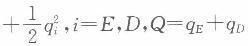
试求:(1)假设两方经理不认识,不共谋,都像短期完全竞争者那样行动,则该情形下的均衡价格和两厂商的均衡产量和利润各是多少?(2)假设两个企业换经理人了,要按照寡头垄断来,使用古诺模型,该情形下的均衡价格和两厂商均衡产量和利润各是多少?(3)E企业知道D企业准备按照古诺均衡来决定产量,现在E企业先按照斯塔克尔伯格模型来决定产量,则该情形下的均衡价格和两厂商的均衡产量和利润各是多少?(4)假设两方经理互相认识,两方共谋,则该情形下的均衡价格和两厂商的均衡产量和利润各是多少?答案:解析:
-
第15题:
假定某寡头厂商面临一条弯折的需求曲线,产量在0~30单位范围内时需求函数为P=60-0.3Q,产量超过30单位时需求函数为P=66 -0.50;该厂商的短期总成本函数为STC=0.005 Q3-0. 2Q2 +36Q +200。 (1)求该寡头厂商利润最大化的均衡产量和均衡价格。 (2)假定该厂商成本增加,导致短期总成本函数变为STC =0.005Q3 -0.2Q2 +50Q +200,求该寡头厂商利润最大化的均衡产量和均衡价格。 (3)对以上(1)和(2)的结果作出解释。
答案:解析:
边际成本函数为MC=0.015Q2 -0.4Q+36。 在Q =30时,边际收益的上限和下限分别为42、36。故在产量为30单位时,边际收益曲线间断部分的范围为36—42。 由厂商的边际成本函数可知,当Q =30时,有MC=37.5。 根据厂商的最大化利润原则,由于MC= 37.5处于边际收益曲线间断部分的范围MR=MC为36—42之内,符合利润最大化原则,所以厂商的产量和价格分别为Q=30、P=51。 (2)厂商边际成本函数为MC =0.015Q2-0. 4Q +50。 当Q =30时,MC= 51.5。 超出了边际收益曲线间断部分的范围36~ 42,此时根据厂商利润最大化原则MR= MC,得Q =20,P=54。 (3)由(1)结果可知,只要在Q=30时MC值处于边际收益曲线间断部分36—42范围之内,寡头厂商的产量和价格总是为Q= 30、P=51,这就是弯折曲线模型所解释的寡头市场的价格刚性现象。 只有边际成本超出了边际收益曲线间断部分36—42的范围,寡头市场的均衡价格和均衡产量才会发生变化。 -
第16题:
美国的波音公司与法国的空客公司都向世界出售民用客机。假设世界对飞机的需求函数为p=20-q,两个公司的成本函数均为c(q)=8q。上问中的结果反映古诺模型假定是否合适?为什么?答案:解析:上述结果反映古诺模型假定合适。古诺均衡解是纳什均衡解,在均衡状态,假定一方的产量不变,另一方为实现利润最大化的产量也不会发生变化。若某一方的产量偏离了均衡状态,双方的利润均会减少,且主动改变产量的一方利润减少更多。在(4)的结果中,美国政府对波音公司进行补贴,从而改变了波音公司的成本函数。在新的古诺均衡中,波音公司的产量增加,而美国作为整体的利润却变为2,小于补贴前的16;同时,空客公司的利润变为9,也小于之前的16,但利润下降幅度比美国少。 -
第17题:
美国的波音公司与法国的空客公司都向世界出售民用客机。假设世界对飞机的需求函数为p=20-q,两个公司的成本函数均为c(q)=8q。问这两个公司是否愿意合谋而平分垄断利润?答案:解析:两个公司愿意合谋并平分利润。 合并后的总利润函数为: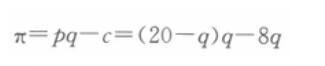
利润最大化的一阶条件为:
解得:q=6,p=14,π=36。 若两个公司平分利润,有π1=π2=18>16,所以两个公司愿意合谋而平分垄断利润。 -
第18题:
美国的波音公司与法国的空客公司都向世界出售民用客机。假设世界对飞机的需求函数为p=20-q,两个公司的成本函数均为c(q)=8q。相对于无补贴的均衡,两个公司各自的利润是否改变?美国政府作为整体,利润是否改变?答案:解析:相对于无补贴,波音公司的利润增加了36 -16 =20,空客公司的利润减少了16-9=7。美国 政府补贴额为3q1=18,美国作为整体,利润增加了20 - 18=2。 -
第19题:
美国的波音公司与法国的空客公司都向世界出售民用客机。假设世界对飞机的需求函数为p=20-q,两个公司的成本函数均为c(q)=8q。(1)相对于无补贴的均衡,两个公司各自的利润是否改变?美国政府作为整体,利润是否改变?
上问中的结果反映古诺模型假定是否合适?为什么?答案:解析:相对于无补贴,波音公司的利润增加了36 -16 =20,空客公司的利润减少了16-9=7。美国 政府补贴额为3q1=18,美国作为整体,利润增加了20 - 18=2。
上述结果反映古诺模型假定合适。古诺均衡解是纳什均衡解,在均衡状态,假定一方的产量不变,另一方为实现利润最大化的产量也不会发生变化。若某一方的产量偏离了均衡状态,双方的利润均会减少,且主动改变产量的一方利润减少更多。在(1)的结果中,美国政府对波音公司进行补贴,从而改变了波音公司的成本函数。在新的古诺均衡中,波音公司的产量增加,而美国作为整体的利润却变为2,小于补贴前的16;同时,空客公司的利润变为9,也小于之前的16,但利润下降幅度比美国少。 -
第20题:
已知某一时期内某商品的需求函数为Q’=50-5P,供给函数为Q=-10+5P (1)求均衡价格Pe和均衡数量Qe,并作出几何图形。 (2)假定供给函数不变,由于消费者收入水平提高,使需求函数变为Qd= 60 -5P。求出相应的均衡价格Pe和均衡数量Qe,并作出几何图形。 (3)假定需求函数不变,由于生产技术水平提高,使供给函数变为Qs= -5 +5P。求出相应的均衡价格Pe和均衡数量Qe,并作出几何图形。 (4)利用(1)、(2)和(3).说明静态分析和比较静态分析的联系和区别。 (5)利用(1)、(2)和(3),说明需求变动和供给变动对均衡价格与均衡数量的影响。答案:解析:(1)已知在均衡价格水平上供给等于需求,将需求函数Qd= 50一5P和供给函数Qs= - 10 +5P代入Qd=Qs,有50 -5P= - 10 +5P,得Pe=6。 把Pe=6代入需求函数Qd =50 -5P,得Qe=50 -5 x6 =20,所以均衡价格和均衡数量分别为Pe=6、Qe=20,如图2-5所示。
(2)消费者收入变化,则需求变化,从而需求曲线向右移动,形成新的均衡。将由于消费者收入水平提高而产生的需求函数Qd=60 -5P和原供给函数Qs= -10 +5P,代入均衡条件Qd= Qs,有60 -5P= - 10 +5P,得Pe =7。 把Pe =7代入Qd =60 -5P,得Q。=60 -5 x7 =25,或者将均衡价格Pe=7代入Qe=- 10 +5P,得Qe= -10 +5 x7= 25。所以,均衡价格和均衡数量分别为Pe=7、Qe=25,如图2-6所示。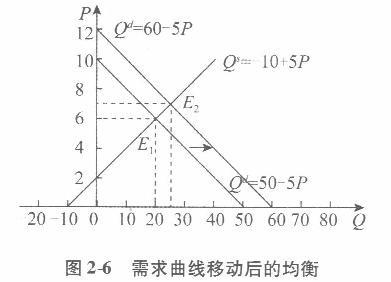
(3)生产技术水平变动,从而供给曲线向右移动,形成新的均衡将原需求函数Qd =50 -5P和由于技术水平提高而产生的供给函数Qs= -5 +5P,代入均衡条件Qd=Qs,有50 - SP=-5 +5P,得Pe= 5.5。 把Pe=5.5代人Qd =50 -5P,得Qe=50 -5 x5.5 =22.5。或者以均衡价格Pe=5.5代入Qs=-5 +5P,得Qe=-5 +5 x5.5 =22.5。所以,均衡价格和均衡数量分别为Pe=5.5、Qe= 22.5,如图2-7所示。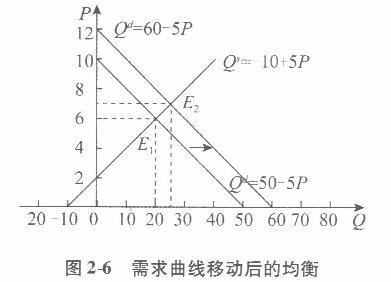
(4)静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。以(1)为例,在图2-5中,均衡点E就是一个体现了静态分析特征的点。它是在给定的供求力量的相互作用下所达到的一个均衡点。在此,给定的供求力量分别用给定的供给函数Qs=- 10 +5P和需求函数Qd =50 -5P表示,均衡点E具有的特征是:均衡价格Pe=6且当Pe=6时,有Qd= Qs =Qe=20;同时,均衡数量Qe=20且当Qe=20时,有Pd=Ps=Pe=6。 依此类推,以上所描述的关于静态分析的基本要点,在(2)及图2-6和(3)及图2-7中的每一个单独的均衡点Ei(i=1,2)都得到了体现。 比较静态分析是考察当原有的条件发生变化时,原有的均衡状态会发生什么变化,并分析比较新旧均衡状态。以(2)为例加以说明。在图2-6中,由均衡点E1变动到均衡点E2,就是一种比较静态分析。它表示当需求增加即需求函数发生变化时对均衡点的影响。比较新、旧两个均衡点E和E2可以很清楚地看到:由于需求增加导致需求曲线右移,最后使得均衡价格由6上升为7,同时,均衡数量由20增加为25。也可以这样理解比较静态分析:在供给函数保持不变的前提下,由于需求函数中的外生变量发生变化,即其中一个参数值由50增加为60,从而使得内生变量的数值发生变化,其结果为均衡价格由原来的6上升为7,同时,均衡数量由原来的20增加为25。类似地,利用(3)及其图2-7也可以说明比较静态分析方法的基本要点。 (5)比较(1)和(2)可得,当消费者收入水平提高导致需求增加,即表现为需求曲线右移时,均衡价格提高了,均衡数量增加了。 比较(1)和(3)可得,当技术水平提高导致供给增加,即表现为供给曲线右移时,均衡价格下降了,均衡数量增加了。 一般地,需求与均衡价格成同方向变动,与均衡数量成同方向变动;供给与均衡价格成反方向变动,与均衡数量成同方向变动。 -
第21题:
已知某一时期内某商品的需求函数为Qd=50-5P,供给函数为Qs=-10+5P。假定需求函数不变,由于生产技术水平提高,使供给函数变为Qs=-5+5P。求出相应的均衡价格Pε和均衡产量Qε。
正确答案: 50-5P=-5+5P
P=5.5
Q=22.5 -
第22题:
已知某一时期内某商品的需求函数为Qd=50-5P,供给函数为Qs=-10+5P。假定供给函数不变,由于消费者收入水平提高,使需求函数变为Qd=60-5P。求出相应的均衡价格Pε和均衡产量Qε。
正确答案: 60-5P=-10+5P
P=7
Q=25 -
第23题:
问答题某竞争行业所有厂商的规模都相等,都是在产量达到500单位时达到长期平均成本的最低点4元,当用最优的企业规模生产600单位产量时,每一个企业的短期平均成本为4.5元,市场需求函数为Q=70000-5000P,供给函数为Q=40000+2500P,求解下列问题: (1)市场均衡价格是多少?该行业处于短期均衡还是长期均衡? (2)当处于长期均衡时,该行业有多少厂商? (3)如果市场需求变化为Q=100000-5000P,求行业与厂商新的短期均衡价格与产量,在新的均衡点,厂商盈利还是亏损?正确答案: (1)由均衡条件知:
70000-5000P=40000+2500P
解得:P=4,Q=50000。
由于均衡价格与长期平均成本的最低点相等,故该行业处于长期均衡。
(2)n=50000/500=100,所以当处于长期均衡时,该行业有100个厂商。
(3)由均衡条件知:
100000-5000P=40000+2500P
得均衡价格P=8,Q=60000。
每个厂商q=60000/100=600,此时厂商的短期平均成本为4.5元,所以厂商盈利(8>4.5)。解析: 暂无解析
