一个竞争性企业只使用一种生产要素z来生产产品y。当0≤z≤4时,企业的生产函数为y=x1.5;当x>4时,企业的生产函数为y= 4+x。如果产品y的价格为每单位1美元,生产要素z的价格为每单位3美元,为使厂商的利润最大化,z的最优投入量为( )。 A.16/9 B.4 C.O D.4/3
题目
B.4
C.O
D.4/3
相似考题
更多“一个竞争性企业只使用一种生产要素z来生产产品y。当0≤z≤4时,企业的生产函数为y=x1.5;当x>4时,企业的生产函数为y= 4+x。如果产品y的价格为每单位1美元,生产要素z的价格为每单位3美元,为使厂商的利润最大化,z的最优投入量为( )。 ”相关问题
-
第1题:
计算题:设某厂商只把劳动作为可变要素,其生产函数为Q=-0.01L3+L2+36L,Q为厂商每天产量,L为工人的日劳动小时数。所有市场均为完全竞争的,单位产品价格为0.10美元,小时工资率为4.8美元,试求当厂商利润极大时:
(1)厂商每天将投入多少劳动小时?
(2)如果厂商每天支付的固定成本为50美元,厂商每天生产的纯利润为多少?
参考答案:(1)因为Q=-0.01L3+L2+36L所以MPP=-0.03L2+2L+36
又因为VMP=MPP•P利润最大时W=VMP
所以0.10(-0.03L2+2L+36)=4.8
得L=60
(2)利润=TR-TC=P•Q-(FC+VC)
=0.10(-0.01•603+602+36•60)-(50+4.8•60)
=22
-
第2题:
将x+y*z中的“+”用成员函数重载,“*”是友元函数重载应写为( )。 A.operator+(operator*(y,z))SX将x+y*z中的“+”用成员函数重载,“*”是友元函数重载应写为( )。
A.operator+(operator*(y,z))
B.x.operator+(operator*(y,z))
C.x.operator+(X*(y,z))
D.x+(operator*(y,z))
正确答案:B
B。【解析】在定义了重载运算符后的函数后,函数operator+重载了运算符“+”。如果在类以外的其他地方定义了一个函数,在类体中用friend对该函数进行声明,此函数就称为本类的友元函数。“*”用友元函数重载就是运算符函数不作为成员函数,而把它放在类外,“*”被改写为“operator*”。“+”为成员函数重载,X.operator+。所以“x+y*z”被改写为“x.operator+(operator*(y,z))”。 -
第3题:
阅读程序段,当输入数据形式为25,13,10时,正确的输出结果为 ______。 int x, y, z; cin>>x>>y>>z;; cout<< "x+y+z=%d\n" <<x+y+z;
A.x+y+z=48
B.x+y+z=35
C.x+z=35
D.不确定值
正确答案:D
-
第4题:
设随机变量(X,Y)的联合密度函数为f(x,y)=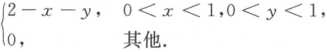 (1)求P(X>2Y);(2)设Z=X+Y,求Z的概率密度函数.
答案:解析:
(1)求P(X>2Y);(2)设Z=X+Y,求Z的概率密度函数.
答案:解析: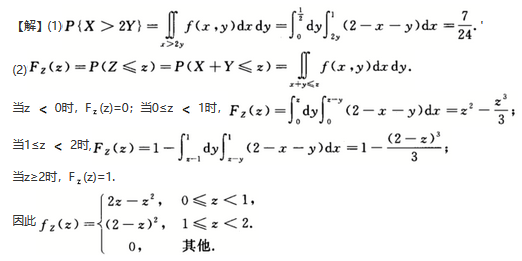
-
第5题:
假设一个地区有两家企业,企业1是上游企业,生产x产品,生产函数为x=g(Lx),其中工表示劳动力投入,企业2是下游企业,生产y产品,其产量不仅取决于自身劳动投入,还取决于企业1的产量x,生产函数为y=h(Ly,x),劳动力的工资为w,x和y产品的价格分别为P1、P2。请证明:在存在外部性的情况下,追求利润最大化的企业会出现无效率的资源配置。答案:解析:

-
第6题:
在一个人(既是消费者又是生产者)的经济e={X,y,ω}中,商品1和商品2在消费和生产中分别满足下面的条件:X一{z∈R2 ▏x1≥2,x2≥0}Y={y∈R2▏y2≤2(-y1)2,y1≤0)。效用函数为U(x1,x2)-(x1-2)x2,初始资源禀赋为ω=(4,0)。 对于价格p=(p1,p2)∈R2++,写出生产者问题并求解最大化利润下的y1和y2。答案:解析:生产者问题可表述为:
构造拉格朗日辅助函数: L=p1y1+p2 y2 +λ1(-y1)+λ2(2y12-y2) 根据K-T条件及经济学含义,得: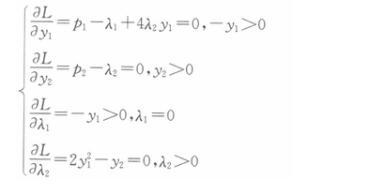
解得:
-
第7题:
企业1生产z,其成本函数为c,(z)一z2+10;企业2生产y,其成本函数为c:(z)=y2+z,可以看出,企业1的产量越大,企业2的成本越高,且两个企业都面临着产品市场的竞争。z的竞争价格为每单位20美元,y的竞争价格为每单位40美元,没有新的企业进入该行业且旧的企业一直存在,则对z征收的有效的庇古税为( )。A.O美元
B.1美元
C.2美元
D.3美元答案:B解析:企业1的私人边际成本为2x,而社会总成本为TC=x2+lO+y2+x,从而生产x的社会边际成本为2x+1。要消除外部效应,应该对每单位x征收庇古税1美元。 -
第8题:
假设商品X的价格为每单位2美元,商品y的价格为每单位3美元,并且商品X的边际效用MUX=y,商品y的边际效用MUY=z,以下消费为内点最优的是( )。A.x=10,y=15
B.x=7.5,y=5
C.x=2,y=4
D.x=6,y=8答案:A解析: -
第9题:
假设某厂商的生产函数为厂
则以下说法哪个是正确的?( )A.该厂商的生产函数呈规模报酬不变
B.成本函数是产出的线性函数
C.如果要素z的价格大于要素y的价格的两倍以上,则只能用要素y进行生产
D.以上说法均不正确答案:D解析:A项,该厂商的生产函数呈规模报酬递增;B项,成本最小化有x=2y,代人生产函数可得
可以看出成本函数不是产出的线性函数;C项,两种要素是完全互补的。 -
第10题:
设x、y、z的值分别为1,2,-3,下面的逻辑运算的值正确的是()
- A、x eq 1 and y eq 2 —为真
- B、x gt y or y gt z —为假
- C、x lt y and y gt z —为假
- D、x eq y or x lt z —为真
正确答案:A -
第11题:
当y处于闭区间[x,z]时,值为真的表达式是()
- A、(y<=z)&&(y>=x)
- B、(x>=y)and(y>=z)c
- C、(x>=y>=z)
- D、(x>=y)&(y>=z)
正确答案:A -
第12题:
单选题将x+y*z中的“+”用成员函数重载,“*”用友元函数重载应写为( )。Aoperator+(operator*(y,z))
Bx.operator+(operator*(y,z))
Cx.operator+(x*(y,z))
Dx+(operator*(y,z))
正确答案: B解析:
函数operator+重载了运算符“+”。“*”用友元函数重载就是运算符函数不作为成员函数,而把它放在类外,“*”被改写为“operator*”。“+”为成员函数重载,x.operator+。所以x+y*z被改写为“x.operator+(operator*(y,z))”。 -
第13题:
下列给定程序中,函数fun()的功能是;计算函数 F(x, y ,z)=(x+ y)/(x-y)+(z+ y)/(z-y)的值。其中x和y不相等,z和y不等。例如,当x的值为9,y的值为11,2的值为15时,函数值为-3.50。
请改正程序中的错误,使它能得出正确的结果。
注意:不要改动main 函数,不得增行或删行,也不得更改程序的结构。
试题程序:
include <stdio. h>
include <math. h>
/**************found******************/
define FU(m, n) (m/n)
float fun(float a, float b, float c)
{ float value;
value=FU(a+ b, a-b)+FU(c+ b, c-b);
/*************found******************/
return(Value);
}
main()
{ float x, y, z, sum;
printf ("Input x y z:: ");
scanf("%f%f%f", &x, &y, &z);
printf("x=%f, y=%f, z=%f\n ",x, y, z);
if (x==y||y==z) {printf ("Data error! \n ");
exit (0); }
sum=fun (x, y, z);
printf("The result is:%5. 2f\n ",sum);
}
正确答案:(1)错误;#define FU(m n) (m/n) 正确:#define FU(mn) (m)/(n) (2)错误:return (Value); 正确:return (value);
(1)错误;#define FU(m, n) (m/n) 正确:#define FU(m,n) (m)/(n) (2)错误:return (Value); 正确:return (value); 解析:如果从数学思想来说,这是一道简单的小学数学题,当然,用C语言的别的办法实现的话,也用不了三两句的程序,但是,这道题的考查点在C语言的宏定义上(这样的问题比较隐蔽),它的格式为#define 标识符字符串,中间要用空格分开,在该题中,标识符为FU (m, n),而字符串则是(m/n),由题干信息易知,应该是# define FU(m,n) (m)/(n)。 -
第14题:
已知(X,Y)服从均匀分布,联合概率密度函数为

设Z=max{X,Y}求Z的概率密度函数fz(z)
答案:X与Y都服从(0, 1)上的均匀分布,则fx与fy在(0, 1)上恒等于1。
Z = z <==> {X = z && Y <= z} + {Y = z && X < z}
因此,fz(z)dz = fx(z)dz * Integrate[fy(z)dy, (0, z)] + fy(z)dz * Integrate[fx(z)dx, (0, z)]
fz(z)dz = zdz + zdz = 2zdz
故fz(z) = 2z,z属于(0, 1). -
第15题:
设有三元方程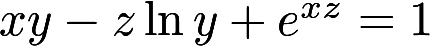 ,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程A.只能确定一个具有连续偏导数的隐函数z=z(x,y)
,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程A.只能确定一个具有连续偏导数的隐函数z=z(x,y)
B.可确定两个具有连续偏导数的隐函数x=x(y,z)和z=z(x,y)
C.可确定两个具有连续偏导数的隐函数y=y(x,z)和z=z(x,y)
D.可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)答案:D解析:
-
第16题:
设随机变量X与Y相互独立,且X服从标准正态分布N(0,1),Y的概率分布为P{Y=0}=P{Y=1}=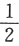 .记Fz(z)为随机变量Z=XY的分布函数,则函数Fz(z)的间断点个数为A.A0
.记Fz(z)为随机变量Z=XY的分布函数,则函数Fz(z)的间断点个数为A.A0
B.1
C.2
D.3答案:D解析:
-
第17题:
小华只消费两种商品X和y,她的收入为500美元,效用函数为U(z,y)=max{z,y),其中,z是商品X的消费量,y是商品Y的消费量。商品Y的价格为1,商品X的价格从1/3上升至2,则等价变化为( )。A.11111美元
B.1566. 67美元
C.1000美元
D.333.33美元答案:D解析:由题意知,小华效用函数为u(x,y)=max{x,y},m=500,py=1,px=1/3,p'x =2,其效用最大化问题为:当px=1/3,py=1时,解得x=1 500,y=0,此时效用“(1 500,0) =max{1 500,0) =1 500。当p'x=2,py=1时,解得x=0,y=500,此时效用u(0,500) =max{0,500)=500。等价变化是以价格变化后的效用水平为基准,计算价格变化对消费者造成的货币损失。在原来的价格下,消费者要达到价格变化后的效用水平所需的货币量记为m',则有:u(3m',O)一max{ 3m',0}一3m'= 500解得:m'=500/3。等价变化为:EV=500/3一500≈一333. 33。 -
第18题:
某消费者对商品x和商品y的效用函数为u(x,y)=x-0.5x2+y。商品x的价格为p,商品y的价格标准化为1。问题:假定商品x由一个具有规模报酬不变生产技术的垄断厂商提供,单位成本为0.4元。求产品定价、消费者剩余、生产者剩余。答案:解析:
-
第19题:
完全竞争市场上,厂商生产要素为x1,x2,面对的是竞争性要素需求市场,两种要素的价格都为2,每个企业的固定成本为64。单个厂商的生产函数为
消费者对该产品的需求函数为Q=280-5p,其中p为产品的市场价格 长期均衡时候企业个数答案:解析:当价格为32时,市场的总需求Q=280-160=120。而单个厂商产量为4,故长期均衡时,企业个数为30个。 -
第20题:
假设在一个竞争性行业中,不同企业的成本函数相同,即当y>0时,f(y)=y2+4,且c(O)=O。 行业的需求函数为D(P) =50-P,其中P是产品y的价格。长期均衡下,该行业最优的企业数量为( )。A.4
B.-23
C.5
D.46答案:B解析: -
第21题:
完全竞争市场上,厂商生产要素为x1,x2,面对的是竞争性要素需求市场,两种要素的价格都为2,每个企业的固定成本为64。单个厂商的生产函数为
消费者对该产品的需求函数为Q=280-5p,其中p为产品的市场价格 长期均衡时的单个企业产量和价格答案:解析:
-
第22题:
为表示“x≥y≥z”,应使用的C语言表达式是()
- A、(x>=y)&&(y>=z)
- B、(x>=y)AND(y>=z)
- C、(x>=y>=z)
- D、(x>=y)&(y>=z)
正确答案:A -
第23题:
单选题设三元函数xy-zlny+exz=1,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程( )。A只能确定一个具有连续偏导数的隐函数z=z(x,y)
B可确定两个具有连续偏导数的隐函数y=y(x,z)和z=z(x,y)
C可确定两个具有连续偏导数的隐函数x=x(y,z)和z=z(x,y)
D可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)
正确答案: C解析:
构造函数F(x,y,z)=xy-zlny+exz-1,则Fx′=y+zexz,Fy′=x-(z/y),Fz′=-lny+xexz。Fx′(0,1,1)=2≠0,Fy′(0,1,1)=-1≠0,Fz′(0,1,1)=0。
故根据隐函数的存在定理可知,方程xy-zlny+exz=1能确定x是y、z的具有连续偏导数的函数x=x(y,z);y是x、z的具有连续偏导数的函数y=y(x,z)。因为Fz′(0,1,1)=0不能满足定理成立的条件,故不能确定z是x、y的具有连续偏导数的隐函数z=z(x,y)。
