某10万人口的城市，政府发放了1 000个出租车运营牌照。为使模型简单，假定每天每辆出租车固定载客300公里。每天运营成本（汽车折旧、劳动力投入等）为300元。设该城市每人每天对出租车的反需求函数为p=32-10q。q为出租车出行的公里数，p为每公里价格。假设出租车市场是竞争性的。 试计算该市场的均衡价格（每公里的均衡价格）和每天均衡的公里数（总里程数）。

当市场均衡时，需求量等于供给量，即5 000-200P=4 000+300P，解得P=2；Q=4600。

(1)根据在完全竞争市场长期均衡时的条件LS =D，即有5500 +300P= 8000 - 200P，解得Pe =5。 把Pe=5代入LS函数，得Q。=5500 +300×5=7000。 所以，市场的长期均衡价格和均衡数量分别为Pe=5、Qe=7000。 (2)同理，根据LS =D，有5500+ 300P =10000 - 200P，解得Pe=9。 以Pe=9代人LS函数，得Qe=5500 +300×9=8200。 所以，市场的长期均衡价格和均衡数量分别为Pe=9、Qe=8200。 (3)比较(1)和(2)可得，对于完全竞争的成本递增行业而言，市场需求增加，会使市场的均衡价格上升，即由Pe=5上升为Pe=9，市场的均衡数量也增加，即由Qe=7000增加为Qe=8200。也就是说，市场需求与均衡价格成同方向的变动，与均衡数量也成同方向的变动。

整个出租车市场每天的利润为π=pQ- TC=2×300 000-300×1 000=300 000（元），即30万元。一年总的预期收入为365×30 -10950（万元），预期收入的现值为：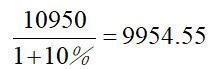

（万元）。由于市场是竞争性的，经济利润为零，所以每个车牌的价格应该为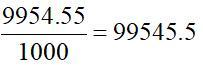

（元）。

(1)已知在均衡价格水平上供给等于需求，将需求函数Qd= 50一5P和供给函数Qs= - 10 +5P代入Qd=Qs，有50 -5P= - 10 +5P，得Pe=6。 把Pe=6代入需求函数Qd =50 -5P，得Qe=50 -5 x6 =20，所以均衡价格和均衡数量分别为Pe=6、Qe=20，如图2-5所示。

(2)消费者收入变化，则需求变化，从而需求曲线向右移动，形成新的均衡。将由于消费者收入水平提高而产生的需求函数Qd=60 -5P和原供给函数Qs= -10 +5P，代入均衡条件Qd= Qs，有60 -5P= - 10 +5P，得Pe =7。 把Pe =7代入Qd =60 -5P，得Q。=60 -5 x7 =25，或者将均衡价格Pe=7代入Qe=- 10 +5P，得Qe= -10 +5 x7= 25。所以，均衡价格和均衡数量分别为Pe=7、Qe=25，如图2-6所示。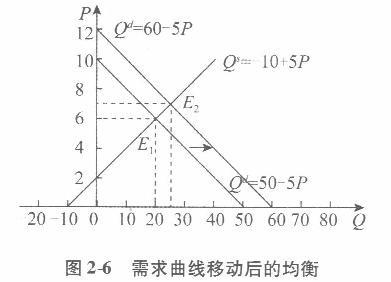

(3)生产技术水平变动，从而供给曲线向右移动，形成新的均衡将原需求函数Qd =50 -5P和由于技术水平提高而产生的供给函数Qs= -5 +5P，代入均衡条件Qd=Qs，有50 - SP=-5 +5P，得Pe= 5.5。 把Pe=5.5代人Qd =50 -5P，得Qe=50 -5 x5.5 =22.5。或者以均衡价格Pe=5.5代入Qs=-5 +5P，得Qe=-5 +5 x5.5 =22.5。所以，均衡价格和均衡数量分别为Pe=5.5、Qe= 22.5，如图2-7所示。

(4)静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。以(1)为例，在图2-5中，均衡点E就是一个体现了静态分析特征的点。它是在给定的供求力量的相互作用下所达到的一个均衡点。在此，给定的供求力量分别用给定的供给函数Qs=- 10 +5P和需求函数Qd =50 -5P表示，均衡点E具有的特征是：均衡价格Pe=6且当Pe=6时，有Qd= Qs =Qe=20；同时，均衡数量Qe=20且当Qe=20时，有Pd=Ps=Pe=6。 依此类推，以上所描述的关于静态分析的基本要点，在(2)及图2-6和(3)及图2-7中的每一个单独的均衡点Ei（i=1，2）都得到了体现。 比较静态分析是考察当原有的条件发生变化时，原有的均衡状态会发生什么变化，并分析比较新旧均衡状态。以(2)为例加以说明。在图2-6中，由均衡点E1变动到均衡点E2，就是一种比较静态分析。它表示当需求增加即需求函数发生变化时对均衡点的影响。比较新、旧两个均衡点E和E2可以很清楚地看到：由于需求增加导致需求曲线右移，最后使得均衡价格由6上升为7，同时，均衡数量由20增加为25。也可以这样理解比较静态分析：在供给函数保持不变的前提下，由于需求函数中的外生变量发生变化，即其中一个参数值由50增加为60，从而使得内生变量的数值发生变化，其结果为均衡价格由原来的6上升为7，同时，均衡数量由原来的20增加为25。类似地，利用(3)及其图2-7也可以说明比较静态分析方法的基本要点。 (5)比较(1)和(2)可得，当消费者收入水平提高导致需求增加，即表现为需求曲线右移时，均衡价格提高了，均衡数量增加了。 比较(1)和(3)可得，当技术水平提高导致供给增加，即表现为供给曲线右移时，均衡价格下降了，均衡数量增加了。 一般地，需求与均衡价格成同方向变动，与均衡数量成同方向变动；供给与均衡价格成反方向变动，与均衡数量成同方向变动。

本题考查均衡价格和均衡产量的含义。当需求价格与供给价格一致时，该价格即为均衡价格，即P=100-4Q=40+2Q，计算得出Q=10,P=60。

(1)单个厂商的边际成本MC =2Q +6。 由短期均衡条件可知P= MC，即P=2Q +6， 即Q =0.5P-3。 故市场的短期供给函数为Qs=100Q= 50P - 300。 (2)联立供给函数与需求函数，可得P=9，Q=150。 (3)征税后，联立函数：

解得Pd=10，Q=120。 故市场短期均衡价格为10，均衡产量为120。 消费者承担1元税收，厂商承受0.6元税收。

边际成本函数为MC=0.015Q2 -0.4Q+36。 在Q =30时，边际收益的上限和下限分别为42、36。故在产量为30单位时，边际收益曲线间断部分的范围为36—42。 由厂商的边际成本函数可知，当Q =30时，有MC=37.5。 根据厂商的最大化利润原则，由于MC= 37.5处于边际收益曲线间断部分的范围MR=MC为36—42之内，符合利润最大化原则，所以厂商的产量和价格分别为Q=30、P=51。 (2)厂商边际成本函数为MC =0.015Q2-0. 4Q +50。 当Q =30时，MC= 51.5。 超出了边际收益曲线间断部分的范围36~ 42，此时根据厂商利润最大化原则MR= MC，得Q =20，P=54。 (3)由(1)结果可知，只要在Q=30时MC值处于边际收益曲线间断部分36—42范围之内，寡头厂商的产量和价格总是为Q= 30、P=51，这就是弯折曲线模型所解释的寡头市场的价格刚性现象。 只有边际成本超出了边际收益曲线间断部分36—42的范围，寡头市场的均衡价格和均衡产量才会发生变化。

当价格为32时，市场的总需求Q=280-160=120。而单个厂商产量为4，故长期均衡时，企业个数为30个。

(1)联立需求函数和供给函数可得：100-2P=20+6P解得：均衡价格P=10。将P=10代入需求函数或供给函数可得销售量为80。 (2)如果政府对该商品征收每单位商品4元的数量税，均衡条件应满足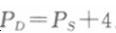

联立以下四个方程：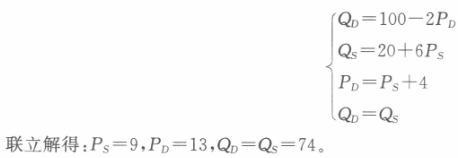

即市场均衡的销售量为74，消费者支付的价格为每单位13元，生产商接受的价格为每单位9元。每单位商品4元的税，其中消费者承担3元，生产者承担1元。 (3)联立需求函数和供给函数可得：100-2P=40+6P解得：均衡价格P=7.5。将P=7.5代入需求函数或供给函数可得销售量为85。如果政府对该商品征收每单位商品4元的数量税，均衡条件应满足PD—PS+4。联立以下四个方程：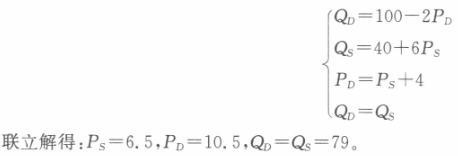

即市场均衡的销售量为79，消费者支付的价格为每单位10.5元，生产商接受的价格为每单位6.5元。每单位商品4元的税，其中消费者承担3元，生产者承担1元。 可以看出，由于供给曲线斜率不变，所以税负的转嫁程度不变，因为税负的转嫁程度取决于需求曲线和供给曲线的斜率。

1.由于 Qd＝300－10P，Qs＝100＋10P，Qs＝Qd，因此有：300－10P＝100＋10P 解方程，得 P0＝10，Q0＝200。
2.①由于 Qd＝500－10P，Qs＝100＋10P，Qs＝Qd，因此有：500－10P＝100＋10P解方程，得 P0＝20，Q0＝300。
②由于 Qd＝300－10P，Qs＝200＋10P，Qs＝Qd，因此有：300－10P＝200＋10P解方程，得 P0＝5，Q0＝250。
3.如果供给不变，需求量增加使需求曲线向右上方移动，导致均衡价格上升，均衡数量增加；相反，需求量减少使需求曲线向左下方移动，使得均衡价格下降，均衡数量减少。
如果需求不变，供给量增加使供给曲线向右下方移动，导致均衡价格下降，均衡数量增加；相反，供给量减少会使供给曲线向左上方移动，使得均衡价格上升，均衡数量减少。