在新古典增长模型中,已知生产函数为y=2k -0. 5k2,y为人均产出,k为人均资本,储蓄率s =0.1。人口增长率n=0.05,资本折旧率δ=0.05。试求: (1)稳态时人均资本和人均产量。 (2)稳态时人均储蓄和人均消费。
题目
在新古典增长模型中,已知生产函数为y=2k -0. 5k2,y为人均产出,k为人均资本,储蓄率s =0.1。人口增长率n=0.05,资本折旧率δ=0.05。试求: (1)稳态时人均资本和人均产量。 (2)稳态时人均储蓄和人均消费。
相似考题
更多“在新古典增长模型中,已知生产函数为y=2k -0. 5k2,y为人均产出,k为人均资本,储蓄率s =0.1。人口增长率n=0.05,资本折旧率δ=0.05。试求: (1)稳态时人均资本和人均产量。 (2)稳态时人均储蓄和人均消费。”相关问题
-
第1题:
根据基本的Solow模型,假设储蓄率为s,人口增长率为n,资本折旧率为δ人均资本为k人均产出为
请回答如下问题: (1)分别考察储蓄率上升和人口增长率上升对均衡状态人均产出的影响,并简要分析影响的传导机制。 (2)推导人均资本增长率的表达式,并通过图形说明初始人均资本越低,则对应的人均资本率越高。答案:解析:本题考查新古典增长模型,属于中央财大“801经济学”必考内容之一。需要重点强调的是,第二小问为高鸿业《西方经济学(宏观部分)》(第6版)教材新增内容。中央财大“801经济学”指定的是第6版教材,建议考生一定要参照第6版教材复习备考。
(1)如图1—3所示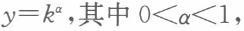
初始储蓄率为s,假设储蓄率上升为s’,C和C'分炳哥带你识真相别是s和s’下的稳态,可以发现当s提高时,y也随之提高。因此,从短期看,更高的储蓄率导致了总产量和人均产量增长率的增加。但是,一旦达到新的稳态,人均产出水平保持不变。 如图1—4所示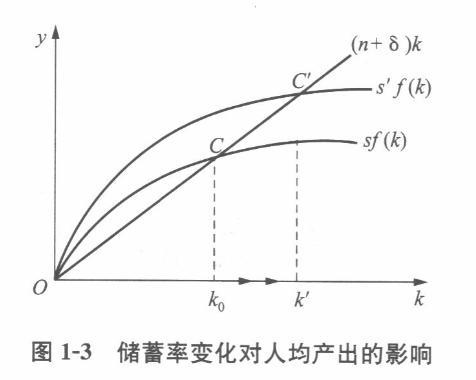
经济最初位于A点的稳态均衡。假定人口增长率从n增加到n’,形成新的稳态为A'。可以看出,人口增长率的增加降低了人均资本的稳态水平,进而降低了人均产出的稳态水平。

如图1—5所示
一个国家的初始人均资本比其稳态水平低得越多,则经济增长得越快;同样,如果一个国家的初始人均资本存量远高于它的稳态水平,那么,它的资本存量将迅速减少,随着这个国家的资本存量逼近稳态水平,资本存量下降的速度将趋近于零。 -
第2题:
在索罗增长模型( Solow model)中,假设生产函数为柯布一道格拉靳函数Y=KaL1-a,已知n、g、б 、a。 (1)写出生产函数的简约形式y=f(k),其中y为人均产出,是为人均资本存量。 (2)已知s值,求解稳定状态下的y*、k*、c*。 (3)当s值未知时,求解黄金规则水平下的稳态y*、k*、s*、c*。答案:解析:
-
第3题:
在新古典增长模型中,人均生产函数为y=f(k) =2k -0.5k2,人均储蓄率为0.3,人口增长率为0.03.求: (1)使经济均衡增长的k值。 (2)与黄金律相对应的人均资本量。答案:解析:(1)新古典增长模型中,经济均衡增长时有sf (k)=nk,代人数值得0.3(2k -0.5k2)=0. 03k,有k=3.8。 (2)由题意,有f(k)=n,于是2-k=0.03,k=1.97,即为与黄金律相对应的稳态的人均资本量。 -
第4题:
给定一国的生产函数Y=(AN)1/2K1/2,A=1,储蓄率为0.6,人口增长率为2%,折旧率为8%。 求出稳态的人均产出,人均资本存量和人均消费水平。答案:解析:
-
第5题:
假定产出是根据含有失业率的生产函数Y= Kα[(l-u*)L]1-α 来表示的。在上式中,K为资本,L为劳动力,u*为自然失业率。国民储蓄率为s,劳动力增长率为n,资本折旧率为δ。 计算该经济的稳态的人均资本和人均产出。答案:解析:
-
第6题:
某国的生产函数为
L为劳动,K为资本,A为技术水平,储蓄率s=0.6,人口增长率n=1%,折旧率d=0. 05,技术进步率
(1)当经济实现平衡增长时,求单位效率人(AL)的资本、收入和消费水平,此时人均收入、人均资本和消费的增长率为多少?总产出和总资本增长率为多少?(2)计算单位效率人的黄金律资本水平,相应的收入、消费及储蓄率水平,说明储蓄率在该模型的作用。(3)如果生产函数变为
其他条件与(1)相同,当经济实现平衡增长时,人均收入和人均资本增长率为多少?总产出和总资本增长率为多少?答案:解析:(1)将生产函数
等式两边同除以
对具有技术进步的新古典增长模型来说,稳态条件为
以及生产函数代人到稳态条件可得:
解得:
单位效率人均收入
单位效率人均消费
当经济实现平衡增长时,人均收入、人均资本和消费的增长率都为技术进步率g,即增长率为4%。总产出和总资本增长率为人口增长率加技术进步率,为4%+1% =5%。(2)在有技术进步的稳态下,单位效率人的黄金律资本水平应满足MPK=n+d+g,即有:
解得:

给定生产函数,一旦确定了相应的储蓄率s,储蓄函数就予以确定,从而就得到稳态下的人均资本和人均产出。因此,问题在于储蓄率的确定,要求确定的储蓄率使得稳态人均消费最大化,即可以通过调整储蓄率从而实现黄金率资本水平。(3)当生产函数变为
时,当经济实现平衡增长时,人均收入和人均资本增长率为0,总产出和总资本增长率为人口增长率,即1%。 -
第7题:
已知新古典增长模型中人均生产函数为y=f(k) =2k-0. 5k2,最为人均资本,储蓄率s为0.4,人口增长率以为0.2%。 请计算: (1)经漭达到稳定状态的值。 (2)黄金律所要求的人均资本k值答案:解析:(1)经济达到稳态时,有k=sy-nk=0,解得k=3.99,即经济达到稳态时的人均资本存量为3. 99,人均产出为0.02。 (2)达到资本黄金律水平时,有MPK =n,解得k=1. 998,所以黄金律水平下的人均资本存量k=l. 998。 -
第8题:
已知生产函数y=k-0.2k2,y为人均产出,k为人均资本存量。储蓄率为0.1,人口增长率为0.05,假设资本折旧为0,稳态时人均产出为()。
- A、1.2
- B、1
- C、1.25
- D、1.5
正确答案:C -
第9题:
假设经济的生产函数为Y=K1/3N1/3,储蓄率和折旧率均为0.10。人均资本的稳态水平是多少?
正确答案: 生产函数为Y=K1/3N2/3,两边同除以N,可得人均生产函数y=f(k)=k1/3
稳态时△k=sf(x)-δk=0即sk1/3=δk
将S=0.1,δ=1.0代入上式可得,k=1 -
第10题:
问答题在新古典增长模型中,人均生产函数为y=f(k)=2k-0.5k*k,人均储蓄率为0.3,设人口增长率为3%。试求经济增长的k值。正确答案: 均衡时有sf(k)=nk,
即0.3*(2k-0.5k^2)=0.03k,
解得k=3.8解析: 暂无解析 -
第11题:
问答题在新古典增长模型中,集约化生产函数为Y=f(k)=2k-0.5k2,人均储蓄率为0.3,设人口增长率为3%,求:(1)使经济均衡增长的k值;(2)黄金分割律所要求的人均资本量。正确答案:
(1)经济均衡增长时,有sf(k)= nk,将s=0.3,n=3%代入,可得:
0.3(2k-0.5k2)=0.03k
化简得:20k-5k2=k,解得:k=3.8。
(2)按黄金分割律要求,对每个人的资本量的选择应使得资本的边际产品等于劳动的增长率,即f′(k)=n。
于是有2-k=0.03,解得k=1.97,即为与黄金率相对应的稳态的人均资本量。解析: 暂无解析 -
第12题:
单选题已知生产函数y=k-0.2k2,y为人均产出,k为人均资本存量。储蓄率为0.1,人口增长率为0.05,假设资本折旧为0,稳态时人均产出为()。A1.2
B1
C1.25
D1.5
正确答案: C解析: 暂无解析 -
第13题:
考虑如下经济模型:生产方程:Y=F(K,L)=KαL1-α其中K为资本存量,L为工人数量。产出的一部分被用于消费,另一部分是储蓄为S。所有的储蓄被用于投资。资本存量的折旧率为ζ。假设技术进步和人口增长均为零。计算稳态时的人均资本量,人均产出和人均消费答案:解析: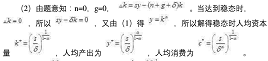
-
第14题:
设在新古典增长模型的框架下,生产函数为Y=F(K,L)=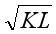
(1)求人均生产函数y=f(k)。 (2)若不存在技术进步,求稳态下的人均资本量、人均产量和人均消费量。答案:解析:
-
第15题:
假设生产函数为Y=KaL1-a,其中,a=l/3,K表示资本,L表示劳动力。 (1)该生产函数是否具有规模收益不变的特征?请解释。 (2)假设该经济的劳动力刚好等于总人口,请将上述生产函数变化成人均产出与人均资本之间的关系。 (3)假设该经济每年的储蓄率为8/25,资本每年的折旧率为2/25。求稳态人均资本和稳态人均产出。 (4)现假设资本折旧率变为1/12,其他假设不变,请问当经济实现稳态时,若要使人均消费最大化,该经济的储蓄率应该是多少?人均消费达到最大化时,该经济的人均资本是多少?此时的人均消费是多少?答案:解析: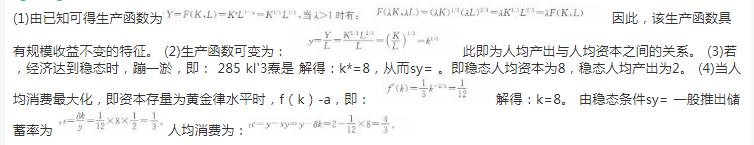
-
第16题:
给定一国的生产函数Y=(AN)1/2K1/2,A=1,储蓄率为0.6,人口增长率为2%,折旧率为8%。
求出黄金律资本量,人均产出和消费量以及相应的储蓄率。答案:解析:
-
第17题:
在新古典增长模型中,人均生产函数为y=
资本折旧率为d=0.04,储蓄率为s-0.2,人口增长率为n=0. 03,技术进步率为g=0. 02。求:(1)经济处于稳态的人均产出和资本存量。(2)黄金律水平下的储蓄率。答案:解析:(1)考虑到技术进步的新古典增长模型经济均衡的稳态条件为:sy-(n_』-d+g)k。将已知条件代入稳态条件可得:加并不改变经济体均衡产出,但由于此时已出现物价上升,故长期中通货膨胀率会上升,对应的长期菲利普斯曲线是一条垂直线。 -
第18题:
假设在Solow模型中,人均生产函数为y=k“5,储存率为s,人口增长率72一0.005,折旧率为d=0. 035。 (1)计算在储蓄率s-0. 16时的稳态人均资本存量。 (2)计算在储蓄率提高到s-0. 41后的稳态人均资本存量(保留一位小数)。答案:解析:(1)当储蓄率s=0. 16,经济达到稳态水平时,有Ak=sy-(n+d)k=0,即:0. 16ko.5 - (0. 005+0. 035)k=0解得稳态人均资本存量为:k*=16。(2)当储蓄率提高到s=0. 41时,经济达到稳态水平时有:0. 41ko.5 - (0. 005+0. 035)k=0解得稳态人均资本存量为:k*≈105.1。经济初始处于稳定状态(k*=16),当储蓄率从0. 16上升到0.41时,储蓄曲线也随之向上移动,储蓄(投资)就高于折旧,于是人均资本存量增加,直到达到k2(k*≈105.1),经济重新达到稳态 -
第19题:
在新古典增长模型中,生产函数为y=f(k)=2k-0. 5k2,人均储蓄率为s-0.3,设人口增长率为3%,求:(1)使经济均衡增长的k值。(2)黄金律所要求的人均资本量。答案:解析:(1)生产函数为y= f(k)一2k -0. 5k2,人均储蓄率为0.3,人口增长率为n=3%。当经济达到稳态时有:△k=s厂(k)-nk=0.3×(2k-0. Sk2)-0. 03k-0解得稳态时的人均资本水平: k-3.8 (2)当经济达到资本黄金律水平时有MPK=n,即有:2-k=3%解得黄金律所要求的人均资本存量为:K*gold=1. 97 -
第20题:
已知某经济社会生产函数y=k-0.2k2,y为人均产出,k为人均资本存量。平均储蓄倾向s为0.1,人口增长率n为0.05,求 (1)均衡资本——劳动比率; (2)均衡人均产出、均衡人均储蓄和均衡人均消费
正确答案:(1)不考虑折旧和技术进步时,在稳定状态有k*=sy-nk=s(k-0.2k2)-nk=0,因k>0,将等式s(k-0.2k2)-nk=0整理,得:k=5-5n/s=2.5,因此,均衡资本——劳动比率为2.5;
(2)将k=2.5代入生产函数中,得到均衡人均产出y=1.25,均衡人均储蓄sy=0.125,均衡人均消费c=y-sy=1.125 -
第21题:
在新古典增长模型中,人均生产函数为y=f(k)=2k-0.5k*k,人均储蓄率为0.3,设人口增长率为3%。试求经济增长的k值。
正确答案:均衡时有sf(k)=nk,
即0.3*(2k-0.5k^2)=0.03k,
解得k=3.8 -
第22题:
问答题假设经济的生产函数为Y=K1/3N1/3,储蓄率和折旧率均为0.10。人均资本的稳态水平是多少?正确答案: 生产函数为Y=K1/3N2/3,两边同除以N,可得人均生产函数y=f(k)=k1/3
稳态时△k=sf(x)-δk=0即sk1/3=δk
将S=0.1,δ=1.0代入上式可得,k=1解析: 暂无解析 -
第23题:
问答题已知某经济社会生产函数y=k-0.2k2,y为人均产出,k为人均资本存量。平均储蓄倾向s为0.1,人口增长率n为0.05,求 (1)均衡资本——劳动比率; (2)均衡人均产出、均衡人均储蓄和均衡人均消费正确答案: (1)不考虑折旧和技术进步时,在稳定状态有k*=sy-nk=s(k-0.2k2)-nk=0,因k>0,将等式s(k-0.2k2)-nk=0整理,得:k=5-5n/s=2.5,因此,均衡资本——劳动比率为2.5;
(2)将k=2.5代入生产函数中,得到均衡人均产出y=1.25,均衡人均储蓄sy=0.125,均衡人均消费c=y-sy=1.125解析: 暂无解析
