求一个与,,都正交的单位向量
题目
求一个与 ,
, ,
, 都正交的单位向量
都正交的单位向量
 ,
, ,
, 都正交的单位向量
都正交的单位向量相似考题
更多“求一个与,,都正交的单位向量”相关问题
-
第1题:
设α=i+2j+3k,β=i-3j-2k,与α、β都垂直的单位向量为( )。A.±(i+j-k)
B.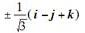
C.
D. 答案:D解析:
答案:D解析:
-
第2题:
已知两点A(4,0,5)和B(7,1,3),则下面与AB方向相同的单位向量e为( )。
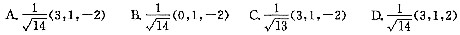 答案:A解析:
答案:A解析: -
第3题:
试求一个正交的相似变换矩阵, 将对称阵 化为对角阵答案:解析:
化为对角阵答案:解析:
-
第4题:
求一个正交变换将二次型 化成标准形答案:解析:
化成标准形答案:解析:
-
第5题:
设二次型
 (b>0),
(b>0),
其中二次型的矩阵A的特征值之和为1,特征值之积为-12.
(1)求a,b的值;
(2)利用正交变换将二次型f化为标准形,并写出所用的正交变换和对应的正交矩阵.答案:解析:
-
第6题:
求一个正交变换把二次曲面的方程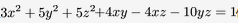 化成标准方程答案:解析:
化成标准方程答案:解析:
-
第7题:
设矩阵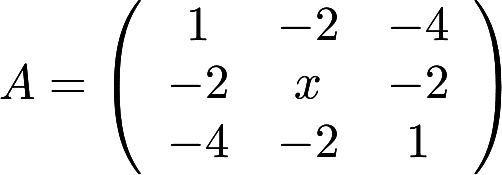 与
与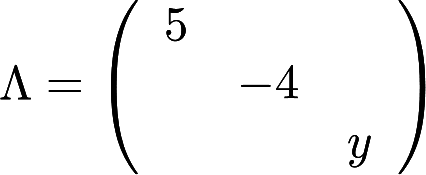 相似,求x, y,并求一个正交阵P,使
相似,求x, y,并求一个正交阵P,使 。答案:解析:
。答案:解析:
-
第8题:
求正交变换,把二次曲面方程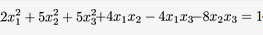 化成标准方程答案:解析:
化成标准方程答案:解析:


-
第9题:
将一个函数通过正交分解映射到正交函数空间的数学变换称为()。
正确答案:正交变换 -
第10题:
正交和极轴追踪是()。
- A、不同的概念
- B、名称不同,但是一个概念
- C、极轴是正交的一个特例
- D、正交是极轴追踪的一个特例
正确答案:D -
第11题:
问答题X为3阶随机矩阵,分别对X进行如下操作: 求X的三角分解;求X的正交分解;求X的特征值分解;求X的奇异值分解;正确答案: >>X=rand(3)
>>[L,U]=lu(X)
>>[Q,R]=qr(X)
>>[V,D]=eig(X)
>>[U,S,V]=svd(X)解析: 暂无解析 -
第12题:
填空题将一个函数通过正交分解映射到正交函数空间的数学变换称为()。正确答案: 正交变换解析: 暂无解析 -
第13题:
设α=i+2j+3k,β=i-3j-2k,则与α,β 都垂直的单位向量为: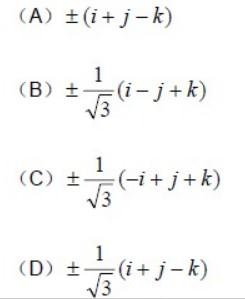 答案:D解析:解:选D。
答案:D解析:解:选D。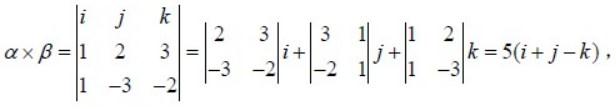
得单位向量为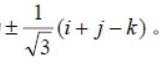
-
第14题:
 ,求正交矩阵T,使
,求正交矩阵T,使 为对角矩阵.答案:解析:
为对角矩阵.答案:解析:

-
第15题:
求一个与 ,
,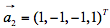 ,
,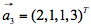 都正交的单位向量答案:解析:
都正交的单位向量答案:解析:

-
第16题:
已知二次型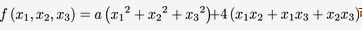 可用正交变换化为
可用正交变换化为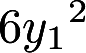 .求a,并且作实现此转化的正交变换答案:解析:
.求a,并且作实现此转化的正交变换答案:解析:


-
第17题:
求一个非零向量a3,使得a3与向量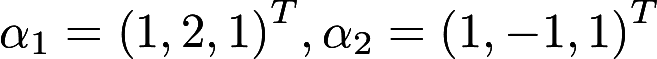 都正交。答案:解析:
都正交。答案:解析:
-
第18题:
已知二次型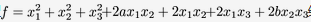 经过正交变换化为标准型
经过正交变换化为标准型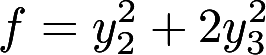 ,求参数a,b及所用的正交变换矩阵答案:解析:
,求参数a,b及所用的正交变换矩阵答案:解析:


-
第19题:
设二次型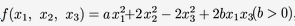 其中二次型矩阵A的特征值之和为1, 特征值之积-12.(1) 求a,b的值; (2) 求一正交变换把二次型
其中二次型矩阵A的特征值之和为1, 特征值之积-12.(1) 求a,b的值; (2) 求一正交变换把二次型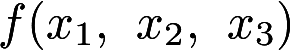 化成标准型(需写出正交变换及标准型)答案:解析:
化成标准型(需写出正交变换及标准型)答案:解析:

-
第20题:
设α=i+2j+3k,β=i-3j-2k,与α、β都垂直的单位向量为( )。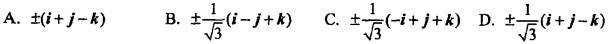 答案:D解析:确答案是D。
答案:D解析:确答案是D。
-
第21题:
X为3阶随机矩阵,分别对X进行如下操作: 求X的三角分解;求X的正交分解;求X的特征值分解;求X的奇异值分解;
正确答案: >>X=rand(3)
>>[L,U]=lu(X)
>>[Q,R]=qr(X)
>>[V,D]=eig(X)
>>[U,S,V]=svd(X) -
第22题:
直流电机的交轴电枢反应中,电枢磁势的轴线().
- A、与几何中性线正交。
- B、与物理中性线正交。
- C、与磁感应线正交。
- D、与主极轴线正交。
正确答案:D -
第23题:
单选题正交和极轴追踪是()。A不同的概念
B名称不同,但是一个概念
C极轴是正交的一个特例
D正交是极轴追踪的一个特例
正确答案: B解析: 暂无解析 -
第24题:
填空题如果一条直线与一个平面垂直,那么称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是____.正确答案: 36解析:
分两种情况:第一种情况:对于每一条棱,都可以与两个侧面构成“正交线面对”,这样的“正交线面对”共有2x12=24个;
第二种情况:对于每一条面对角线,都可以与一个对角面构成“正交线面对”,这样的“正交线面对”共有12个.故正方体中“正交线面对”共有24+12=36个.
