甲、乙两项工程分别由一、二工程队负责完成,晴天时,一队完成甲工程需要12天,二队完成乙工程需要15天,雨天时,一队的工作效率是晴天时的60%,二队的工作效率是晴天时的80%,结果两队同时开工并同时完成各自的工程,那么,在这段施工期间雨天的天数为（ ）A.8 B.10 C.12 D.15 E.以上选项均不正确

第1题：

第2题：

第3题：

第4题：

答案：C

解析：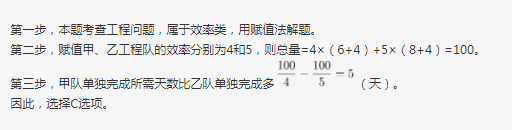

第5题：

甲、乙两个工程队合作完成某工程需36天，若甲工程队先做10天，剩下的工程再由两队合作30天完成。问乙工程队的工作效率是甲工程队的：

第6题：

第7题：

第8题：

夏天干旱，甲、乙两家请人来挖井，阴天时，甲家挖井需要8天，乙家需要10天；晴天时，甲家工作效率下降40%，乙家工作效率下降20%，两家同时开工并同时挖好井，问甲家挖了几个晴天（）

• A、2天
• B、8天
• C、10天
• D、12天

第9题：

第10题：

第11题：

答案：C

解析：

(1)A、B两队分别完成甲、乙两项工程的工效如下表：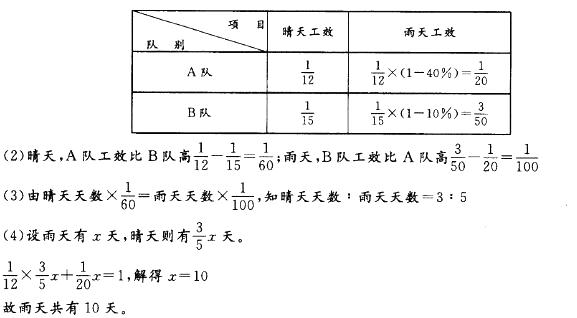

第12题：

答案：D

解析：

第一步，本题考查工程问题，用赋值法解题。
第二步，甲队单独施工30天可以完成该项工程的



，那么甲队单独施工90天可以完成该项工程，而甲队施工30天后，乙队加入，再同时施工15天可完成该项工程，可列方程：90甲＝30甲＋（甲＋乙）×15，解得，乙＝3甲，即甲乙效率之比为1∶3，赋值甲队的效率为1，那么乙队的效率为3，该项工程的总量为1×90＝90。
第三步，要使乙队施工天数尽可能少，则甲队施工天数应该尽可能多，而甲队施工时间不能超过36天，则让甲队施工36天，完成1×36＝36，该项工程还剩90－36＝54，乙队需要



（天）。

第13题：

答案：C

解析：

设甲、乙两项工程的总工程量均为1，则在晴天A队的工作效率为，B队的工作效率为；在雨天A队的工作效率为×(1-40％)，B队的工作效率为×(1-10％)。设在整个施工日子里。雨天共有x天，列方程：

解之得：x=10

第14题：

答案：C

解析：

第15题：

答案：A

解析：

第一步，本题考查工程问题，属于时间类，用赋值法解题。
第二步，结合题意赋总量为12，由“甲、乙、丙合作一天完成了工程的”，可知效率有：甲＋乙＋丙＝12×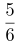＝10①，由“甲、乙、丙单独完成这项工程所用时间均为整数天数”，可得：12÷甲 ②、12÷乙③、12÷丙④均为整数，由②③④可得甲、乙、丙效率可能的取值为1、2、3、4、6等，由①及“甲单独完成这项工程所用天数大于乙，乙所用天数大于丙”，得效率：甲＝1，乙＝3，丙＝6满足题意。
第三步，甲、乙合作完成整个工程需要＝3（天）。
因此，选择A选项。

第16题：

第17题：

答案：A

解析：

本题属于工程问题。
设甲工程队的效率为x，乙工程队的效率为y。根据工程总量不变可列式：36×（x+y）=10x+30×（x+y），化简得2x=3y，即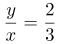}，即乙工程队的工作效率是甲工程队的{图1。
因此，选择A选项。

第18题：

甲、乙、丙三个工程队合作18天可以完成一项工程。乙队与丙队的工作效率相同，甲队3天的工作量与乙队2天的工作量相当。现在该工程先由甲、丙两队合作若干天后再交由乙、丙两队合作完成，共用时26天。那么，丙工程队完成的工作量占全部工程的（）

• A、1/2
• B、13/24
• C、26/63
• D、5/9

第19题：

第20题：