某次数学竞赛准备22支铅笔作为奖品发给获得一、二、三等奖的学生,原计划一等奖每人发6支,二等奖每人发3支,三等奖每人发2支,后又改为一等奖每人发9支,二等奖每人发4支,三等奖每人发1支,则得一等奖的学生有（ ）人A.1 B.2 C.3 D.4 E.5

题目
某次数学竞赛准备22支铅笔作为奖品发给获得一、二、三等奖的学生,原计划一等奖每人发6支,二等奖每人发3支,三等奖每人发2支,后又改为一等奖每人发9支,二等奖每人发4支,三等奖每人发1支,则得一等奖的学生有（ ）人

A.1
B.2
C.3
D.4
E.5
相似考题

1.：在一次射击练习中，甲、乙、丙三位战士各打了四发子弹，全部中靶，其命中情况如下： ①每人四发子弹所命中的环数各不相同； ②每人四发子弹所命中的总环数均为17环； ③乙有两发命中的环数分别与甲其中两发一样，乙另两发命中的环数与丙其中两发一样； ④甲与丙只有一发环数相同； ⑤每人每发子弹的最好成绩不超过7环。 问：甲与丙命中的相同环数是几环？（ ）A．1B．5C．6D．11

2.公司举办“我爱奥运”演讲竞赛，一共有1人获得一等奖，2人获得二等奖，3人获得三等奖，获得二等奖的男员工有1人，问得奖员工中没有获得一等奖的女员工最少有多少，最多有多少?（ ）A．1，4B．2，3C．0，5D．3，2

3.一笔奖金分一等奖、二等奖和三等奖，每个一等奖的奖金是每个二等奖奖金的两倍，每个二等奖的奖金是每个三等奖奖金的两倍。如果评一、二、三等奖各两人，那么每个一等奖金是308元；如果评一个一等奖，三个三等奖，两个二等奖，那么每个一等奖的奖金是多少元?（ ）A．154B．196C．392D．490

4.报社将一定的奖金分发给征文活动获奖者，其中一等奖学金是二等的2倍，二等奖学金是3等的1.5倍，如果一、二、三等奖学各评选两人，那么一等奖获得者将得2400元奖金；如果一等奖只评选一人，二、三等奖各评选两人，那么一等奖的奖金是（）A. 2800元 B. 3000元 C. 3300元 D. 4500元

更多“某次数学竞赛准备22支铅笔作为奖品发给获得一、二、三等奖的学生,原计划一等奖每人发6支,二等奖每人发3支,三等奖每人发2支,后又改为一等奖每人发9支,二等奖每人发4支,三等奖每人发1支,则得一等奖的学生有（ ）人”相关问题

  • 第1题：

    将铅笔若干支分给学生数人，若每人分10支则余48支；若每人分13支则差24支，问每人分几支正好分完？（ ）。

    A．12

    B．11

    C．10

    D．14


    正确答案：A

    设共有x名学生，则10x+48=13x一24，解得x=24，则共有24×10+48＝288支铅笔，要正好分完，每人应分铅笔288÷24=12(支)。

  • 第2题：

    某次数学竞赛准备了22支铅笔作为一、二、三等奖的奖品，原计划一等奖每人发6支，二等奖每人发3支，三等奖每人发2支。后来又改为一等奖每人发9支，二等奖每人发4支，三等奖每人发1支。问共有多少人获奖?

    A．3

    B．6

    C．8

    D．10


    正确答案：C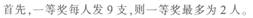



  • 第3题：

    某晚会计划设置抽奖环节，能用于购买奖品的总金额固定，且要求每名一等奖奖品的金额是二等奖的两倍，每名二等奖奖品的金额是三等奖的两倍。如果一、二、三等级各设置两名，则一等奖奖品金额为每名720元。若一等奖设一名、二等奖两名、三等奖四名，则一等奖的奖品金额为每名多少元：

    A780
    B840
    C880
    D940


    答案：B
    解析：

  • 第4题：

    90名参加军训的学生进行射击训练，其中高中生每人射击20发手枪子弹，本科生每人射击10发步枪子弹和20发手枪子弹，研究生每人射击20发步枪子弹和30发手枪子弹。若所有学生共消耗步枪子弹800发，手枪子弹2100发，则参加射击训练的本科生比研究生：

    A.多20人
    B.少20人
    C.多10人
    D.少10人

    答案：D
    解析：
    第一步，本题考查基础应用题，用方程法解题。
    第二步，由高中生射击20发手枪子弹，本科生射击10发步枪和20发手枪子弹，研究生每人射击20发步枪子弹和30发手枪子弹，分别设高中生、本科生和研究生人数为x、y和z，可得x+y+z=90；根据共消耗步枪子弹800发，可得10y+20z=800；根据共消耗手枪子弹2100发，可得20x+20y+30z=2100。
    第三步，解得x＝40，y＝20，z=30，故本科生比研究生少10人。
    因此，选择D选项。

  • 第5题：

    一次数学竞赛准备了22支铅笔作为奖品发给获得一、二、三等奖的学生，原计划发给一等奖每人6支，二等奖每人3支，三等奖每人2支，后来改为一等奖每人9支，二等奖每人4支，三等奖每人1支，获得三等奖的学生有几人?

    A.2
    B.3
    C.4
    D.5

    答案：D
    解析：
    设获一、二、三等奖的学生各a,b、c人，由题意可得，6a+3b+2c=9a+4b+c=22，则有3a+b—c=0，即c=3a+b，代人方程可得，l2a+5b=22。12a是偶数，则56也是偶数，推出a=1，b=2，c=3a+b=5，应选择D。

  • 第6题：

    老师拿来一箱笔记本让班长负责给同学们分发，如果每人发2本，还剩22本，如果每人发3本，就少15本，该班共有多少学生？

    A.37
    B.34
    C.23
    D.17

    答案：A
    解析：
    第一步，本题考查基础应用题，用方程法解题。
    第二步，设班级共有学生x人，可列方程得2x＋22＝3x－15，解得x＝37。
    因此，选择A选项。

  • 第7题：

    局技术创新奖分为以下奖项：（）。

    • A、一等奖
    • B、二等奖
    • C、三等奖
    • D、攻关奖

    正确答案:A,B,C

  • 第8题：

    优秀学生奖学金的等级和金额是（）

    • A、特等奖学金每人每年2000元，一等奖学金每人每年1000元，二等奖学金每人每年500元
    • B、特等奖学金每人每学期2000元，一等奖学金每人每学期1000元，二等奖学金每人每学期500元
    • C、特等奖学金每人每学期1000元，一等奖学金每人每学期500元，二等奖学金每人学期200元
    • D、特等奖学金每人每学期500元，一等奖学金每人每学期300元，二等奖学金每人每学期200元

    正确答案:B

  • 第9题：

    优秀学生综合奖学金一等奖为每人每年多少元？（）

    • A、300
    • B、400
    • C、500
    • D、600

    正确答案:C

  • 第10题：

    团体旅客如填发代用票时，（）。

    • A、按团体旅客人数每人发一张团体旅客证
    • B、除代用票持票本人外，每人另发一张团体旅客证
    • C、编制客运记录注明
    • D、按团体旅客人数，每人打印一张签证号

    正确答案:B

  • 第11题：

    单选题
    一笔奖金分一等奖、二等奖和三等奖，每个一等奖的奖金是每个二等奖奖金的两倍，每个二等奖的奖金是每个三等奖奖金的两倍。如果评一、二、三等奖各两人，那么每个一等奖金是308元；如果评一个一等奖，三个三等奖，两个二等奖，那么一等奖的奖金是多少元（）
    A

    154

    B

    196

    C

    392

    D

    490


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    莱次数学竞赛准备了22支铅笔作为一，二，三等奖的奖品，原计划一等奖每人发6支，二等奖每人发3支，三等奖每人发2支。后来又改为一等奖每人发9支，二等奖每人发4支，三等奖每人发1支。问共有多少人获奖？（　　）
    A

    3

    B

    6

    C

    8

    D

    10


    正确答案： B
    解析：
    由“一等奖每人发9支”可知，一等奖最多为2人。若一等奖有2个人，则9×2十4十1＞22，则获得一等奖的只有1人，设获得二等奖的有x人，三等奖的有y人，列方程6＋3x＋2y＝22，9＋4x＋y＝22，得x＝2，y＝5，则获奖的人数一共有1＋2＋5＝8人。

  • 第13题：

    给学生分铅笔，三分之一的学生每人分4支，其余的每人分5支，则还剩余5支；若有2个学生每人分7支，给其余人每人分6支，则缺13支。请问一共有多少支铅笔?（ ）

    A．47

    B．52

    C．57

    D．61


    正确答案：D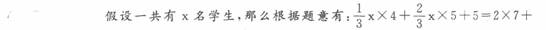


  • 第14题：

    某学校组织一次教工接力比赛，共准备了25件奖品分发给获得一、二、三等奖的职工，为设计获得各级奖励的人数，制定两种方案：若一等奖每人发5件，二等奖每人发3件，三等奖每人发2件，刚好发完奖品；若一等奖每人发6件，二等奖每人发3件，三等奖每人发1件，也刚好发完奖品，则获得二等奖的教工有多少人：
    A6
    B5
    C4
    D3


    答案：A
    解析：

  • 第15题：

    将一批本子发给学生，若每人发10本，则差90本；若每人发8本，则仍差8本。有多少学生和多少本子?（）
    A.40人、320本
    B.42人、300本
    C.41人、320本
    D.40人、300本


    答案：C
    解析：
    此题为两次都不足(亏)，人数为(90—8)÷(10一8)=41人，有本子10×41—90=320本．

  • 第16题：

    某单位为业务技能大赛获奖职工发放奖金，一、二、三等奖每人奖金分别为800、700、500元。11名获一、二、三等奖的职工共获奖金6700元，问有多少人获得三等奖？（）

    A.3人
    B.4人
    C.5人
    D.6人

    答案：D
    解析：
    假设一、二、三等奖的人数分别是a,b,c，则800a+700b+500c=6700,a+b+c=11,两个式子化简得到3a+2b=12,根据3的倍数得到b=3,所以a=2,c=6。

  • 第17题：

    某班级有甲、乙、丙三位同学参加奥数竞赛，获一、二、三等奖的各有一人。班主任猜测：甲肯定是一等奖，乙肯定不是一等奖，丙肯定不是三等奖。事实上，班主任只猜中了一个。
    据此，可推知获得二等奖的是：

    A.甲同学
    B.乙同学
    C.丙同学
    D.无法判断

    答案：C
    解析：
    第一步，确定题型。
    题干有信息匹配特征，确定为分析推理。
    第二步，分析条件，进行推理。
    已知班主任只猜对了一个，同时选项信息较少，考虑使用假设法。
    假设“甲肯定是一等奖”为真，那么“乙肯定不是一等奖”也为真，出现两句话为真，与题干矛盾，该假设不成立，第一句话为假，故甲不是一等奖；
    假设“乙肯定不是一等奖”为真，那么“甲肯定是一等奖”为假，甲和乙都不是一等奖，可知丙是一等奖，那么“丙不是三等奖”为真，出现两句话为真，与题干矛盾，该假设不成立，第二句话为假，故乙是一等奖。
    前两句话均为假，第三句话为真。
    综上，乙是一等奖，丙是二等奖，甲是三等奖。
    因此，选择C选项。

  • 第18题：

    报社将一定的奖金分发给征文活动获奖者，其中一等奖学金是二等的2倍，二等奖学金是三等的1.5倍，如果一、二、三等奖学各评选两人，那么一等奖获得者将得2400元奖金；如果一等奖只评选一人，二、三等奖各评选两人，那么一等奖的奖金是：
    A 2800元
    B 3000元
    C 3300元
    D 4500元


    答案：C
    解析：

  • 第19题：

    参加全国中学生学科竞赛，在省赛区获得（）以及获得全国决赛（），并要求转入竞赛学科相同或相近专业者，可以允许转专业。 

    • A、特等奖、三等奖
    • B、一等奖、一等奖
    • C、特等奖、一等奖
    • D、一等奖、三等奖及以上

    正确答案:D

  • 第20题：

    湖南师范大学综合奖学金每学年评定一次，特等奖学金每人每年（）元；一等奖学金每人每年（）元；二等奖学金每人每年（）元；三等奖学金每人每年（）元。

    • A、3000；2000；1000；500
    • B、5000；1500；1000；500
    • C、3000；1500；1000；500
    • D、4000；2000；1000；500

    正确答案:C

  • 第21题：

    如果某同学在英语竞赛中的标准得分为2，并且知道1%为一等奖，5%为二等奖，10%为三等奖，则他（）

    • A、获一等奖
    • B、获二等奖
    • C、获三等奖
    • D、无缘奖项

    正确答案:D

  • 第22题：

    单选题
    团体旅客如填发代用票时，（）。
    A

    按团体旅客人数每人发一张团体旅客证

    B

    除代用票持票本人外，每人另发一张团体旅客证

    C

    编制客运记录注明

    D

    按团体旅客人数，每人打印一张签证号


    正确答案： A
    解析： 暂无解析

  • 第23题：

    单选题
    如果某同学在英语竞赛中的标准得分为2，并且知道1%为一等奖，5%为二等奖，10%为三等奖，则他（）
    A

    获一等奖

    B

    获二等奖

    C

    获三等奖

    D

    无缘奖项


    正确答案： D
    解析： 暂无解析

相关内容