以直线y十x=0为对称轴且与直线y-3x=2对称的直线方程为（ ）

题目
以直线y十x=0为对称轴且与直线y-3x=2对称的直线方程为（ ）

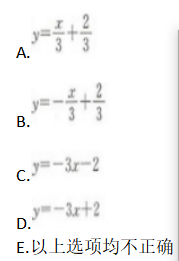
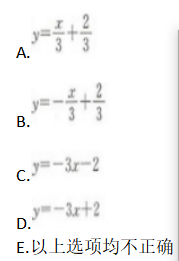
相似考题

1.已知曲线C为y= 2x2，直线l为y= 4x．（10分）(1)求由曲线C与直线l所围成的平面图形的面积S；(2)求过曲线C且平行于直线l的切线方程．

2.直线z的方程为x-y-2=0，它关于点(1，-4)的对称直线方程为A．x+y-8=0B．x-y-8=0C．z+y+8=0D．x-y+8=0

3.斜率为2,且过点(－3,5)的直线方程为()A、y-2x-1=0B、y-2x=7=0C、2y-x-1=0D、y-2x-11=0

4.过点（2，1）且与直线y=0垂直的直线方程为 （ ）A.z=2B.x=1C.y=2D.y=1

更多“以直线y十x=0为对称轴且与直线y-3x=2对称的直线方程为（ ） ”相关问题

  • 第1题：

    设平面方程为x+y+z+1=0，直线方程为1－x=y+1=z，则直线与平面：

    A.平行
    B.垂直
    C.重合
    D.相交但不垂直

    答案：D
    解析：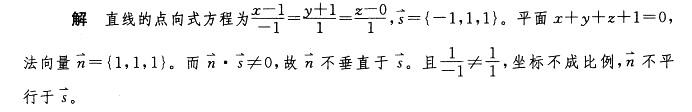

  • 第2题：

    设直线方程为x=y-1=z，平面方程为x-2y+z=0，则直线与平面：
    A.重合 B.平行不重合
    C.垂直相交 D.相交不垂直


    答案：B
    解析：
    从而知直线//平面或直线与平面重合；再在直线上取一点（0,1,0），验证该点是否满足平面方程。

  • 第3题：

    圆心在Y轴上，且与直线χ+y-3=0及χ-y-1=0都相切的圆的方程为_____．


    答案：
    解析：
    【答案】
    【考情点拨】本题主要考查的知识点为圆的切线的性质．
    【指导指导】设圆的方程为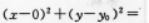r2(如图)

  • 第4题：

    过直线3x＋2y＋1＝0与2x－3y＋5＝0的交点，且垂直于直线L：6x－2y＋5＝0的直线方程是（　　）

    A.x－3y－2＝0
    B.x＋3y－2＝0
    C.x－3y＋2＝0
    D.x＋3y＋2＝0

    答案：B
    解析：

  • 第5题：

    与已知直线7x+24y-5=0平行，且距离等于3的直线方程是。


    答案：
    解析：
    7x+24y+70=0或7x+24y-80=0

  • 第6题：

    设圆C与圆（x-5）2+y2=2关于直线y=2x对称，则圆C的方程为



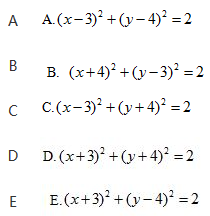    答案：E
    解析：

  • 第7题：

    经过圆x2+2x+y2=0的圆心，与直线x+y=0垂直的直线方程是（）。

    • A、x+y+1=0
    • B、x-y-1=0
    • C、x+y-1=0
    • D、x-y+1=0

    正确答案:D

  • 第8题：

    因为回归直线是根据回归方程所求得，所以必然出现下列情况（）

    • A、回归直线必然通过点（'X，'Y）
    • B、当X为任何数时，均可在回归直线上找到相应的Y值
    • C、当a大于0时，回归直线与纵轴相交处，Y值必为正值
    • D、当a大于0时，回归直线与纵轴相交处，Y值必为负值
    • E、当b等于0时，回归直线与横轴重合

    正确答案:A,C

  • 第9题：

    单选题
    直线y＝kx＋b（k≠0），关于直线x＋y＝0对称的直线方程为（　　）．
    A

    x＋ky＋b＝0

    B

    x＋ky－b＝0

    C

    x－ky－b＝0

    D

    x－ky＋b＝0


    正确答案： B
    解析：
    令x＝－y，y＝－x，将其代入直线y＝kx＋b中，则关于直线x＋y＝0对称的直线方程为x－ky＋b＝0．

  • 第10题：

    单选题
    过点（2，1）且与直线y＝0垂直的直线方程为（　　）．
    A

    x＝2

    B

    x＝1

    C

    y＝2

    D

    x＝1


    正确答案： D
    解析：
    直线y＝0即为x轴，所求直线要与x轴垂直，即为x＝2．

  • 第11题：

    单选题
    经过圆x2+2x+y2=0的圆心，与直线x+y=0垂直的直线方程是（）。
    A

    x+y+1=0

    B

    x-y-1=0

    C

    x+y-1=0

    D

    x-y+1=0


    正确答案： B
    解析： 圆x2+2x+y2=0的圆心是（-1，0），与直线x+y=0垂直的直线方程的斜率为1，可求得此直线方程为x-y+1=0。

  • 第12题：

    单选题
    设直线的方程为x=y-1=z，平面的方程为x-2y+z=0,则直线与平面（ ）
    A

    重合

    B

    平行不重合

    C

    垂直相交

    D

    相交不垂直


    正确答案： C
    解析：

  • 第13题：

    设曲线y=y(x)上点P(0，4)处的切线垂直于直线x-2y+5=0，且该点满足微分方程y″+2y′+y=0，则此曲线方程为( )。

    A.
    B.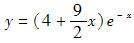
    C.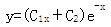
    D.

    答案：D
    解析：

  • 第14题：

    若直线ax+y+5=0，与直线x-2y+7=0垂直，则a的值为______ 。


    答案：
    解析：
    两直线垂直时，斜率之积为-1。计算可得a=2。

  • 第15题：

    过点(0，1)且与直线x+y+1=0垂直的直线方程为()

    A.y=x
    B.y=2x+1
    C.y=x+1
    D.y=x-1

    答案：C
    解析：

  • 第16题：

    直线2x+5y-6=0关于y轴对称的直线方程是（ ）

    A.2x-5y+6=0
    B.2x-5y-6=0
    C.5x+2y-6=0
    D.2x+5y+6=0

    答案：A
    解析：
    【考情点拨】本题主要考查的知识点为直线的对称牲． 【应试指导】设直线2x+5y-6=0上任一点P(x，y)关于y轴的对称点P'(-x，y)，把点P'(-x，y)的坐标代入方程2x+5y-6=0整理得所求直线方程是2x-5y+6=0．

  • 第17题：

    直线2x-3y+1=0关于直线x=1对称的直线方程是（ ）

    A.2x-3y+1=0
    B.2x+3y-5=0
    C.3x+2y-5=0
    D.3x-2y+5=0
    E.3x-2y-5=0

    答案：B
    解析：
    设点（x,y）在所求直线上,诚点关于x=1对称的点为（2-x,y）,由于点（2-x,y）在直线2x-3y+1=0上,所以有2×（2-x）-3y+1=0,化简得2x+3y-5=0.

  • 第18题：

    设直线的方程为x=y-1=z， 平面的方程为x-2y+z=0，则直线与平面（ ）。
    A.重合 B.平行不重合 C.垂直相交 D.相交不垂直


    答案：B
    解析：
    正确答案为B。
    提示：直线的方向向量为s = (1，1，1)，平面的法向量为n= (1，-2，1)，s·n = 1-2 + 1 = 0,这两个向量垂直，直线与平面平行，又直线上的点(0，1，0)不在平面上，故直线与平面不重合。

  • 第19题：

    已知直线经过（x1，y1）点，斜率为k(k≠0)，则直线方程为y=2kx+2。


    正确答案:错误

  • 第20题：

    设直线的方程为x=y-1=z，平面的方程为x-2y+z=0，则直线与平面（）。

    • A、重合
    • B、平行不重合
    • C、垂直相交
    • D、相交不垂直

    正确答案:B

  • 第21题：

    填空题
    曲线y＝y（x）经过原点且在原点处的切线与直线2x＋y＝6平行，而y＝y（x）满足方程y″－2y′＋5y＝0，则此曲线的方程为____。

    正确答案： y=-exsin2x
    解析：
    所求曲线方程满足方程y″－2y′＋5y＝0，其特征方程为r2－2r＋5＝0，解得r1，2＝1±2i。故方程y″－2y′＋5y＝0的通解为y＝ex（c1cos2x＋c2sin2x）。又因为所求曲线经过原点，且在原点处的切线与直线2x＋y＝6平行，故y（0）＝0，y′（0）＝－2，将其代入y＝ex（c1cos2x＋c2sin2x）得c1＝0，c2＝－1。故所求曲线方程为y＝－exsin2x。

  • 第22题：

    单选题
    设直线方程为x=y-1=z，平面方程为x-2y+z=0，则直线与平面（　　）。[2011年真题]
    A

    重合

    B

    平行不重合

    C

    垂直相交

    D

    相交不垂直


    正确答案： C
    解析：
    直线的方向向量s＝（1，1，1），平面的法向向量n＝（1，－2，1），其向量积s·n＝1－2＋1＝0，则这两个向量垂直，即直线与平面平行。又该直线上的点（0，1，0）不在平面上，故直线与平面不重合。

  • 第23题：

    单选题
    过点（1，2）且与直线2x＋y－3＝0平行的直线方程为（　　）．
    A

    2x＋y－5＝0

    B

    2y－x－3＝0

    C

    2x＋y－4＝0

    D

    2x－y＝0


    正确答案： B
    解析：
    设和2x＋y－3＝0平行的直线方程为2x＋y＋c＝0，将（1，2）代人，则有2×1＋2＋c＝0，得c＝－4．

相关内容