某次网球比赛的四强对阵为甲对乙、丙对丁,两场比赛的胜者将争夺冠军.选手之间相互获胜的概率如下:甲获得冠军的概率为A.0.165 B.0.245 C.0.275 D.0.315 E.0.330
题目
某次网球比赛的四强对阵为甲对乙、丙对丁,两场比赛的胜者将争夺冠军.选手之间相互获胜的概率如下:
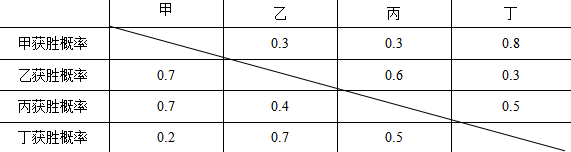
甲获得冠军的概率为

甲获得冠军的概率为
A.0.165
B.0.245
C.0.275
D.0.315
E.0.330
B.0.245
C.0.275
D.0.315
E.0.330
相似考题
更多“某次网球比赛的四强对阵为甲对乙、丙对丁,两场比赛的胜者将争夺冠军.选手之间相互获胜的概率如下: ”相关问题
-
第1题:
甲、乙、丙、丁四人开展羽毛球比赛,首轮每人需和另外3人各比1场,获胜2场及以上者进入下一轮,否则淘汰。甲胜乙、丙、丁的概率分别为70%、50%、40%,问甲首轮遭淘汰的概率是多少A.42.5%
B.45%
C.47.5%
D.48%答案:B解析:第一步,获胜2场及以上者进入下一轮,那么如果甲首轮遭淘汰,说明甲输了2场或者3场。第二步,(1)甲输三场的概率为0.3×0.5×0.6=0.09;(2)甲输两场有三种可能:a.赢乙输丙丁,概率为0.7×0.5×0.6=0.21;b.赢丙输乙丁,概率为0.3×0.5×0.6=0.09;c.赢丁输乙丙,概率为0.3×0.5×0.4=0.06;所以甲首轮遭淘汰的概率为0.09+0.21+0.09+0.06=0.45。因此,选择B选项。 -
第2题:
甲、乙、丙、丁、戊、已、庚、辛8名乒乓球爱好者随机分成4个双打组合,随机分配对手两两比赛,两场比赛的胜者进行决赛。如每个组合对其他任意组合的胜率都是50%,问甲所在队伍在决赛中战胜丙所在队伍的概率在以下哪个范围内?( )A.低于3%
B.在3%-5%之间
C.在5%-8%之间
D.高于8%答案:C解析:第一步,本题考查概率问题,属于分类分步型。
第二步,根据题意要使甲所在队伍决赛中战胜丙所在队伍,那么在第一轮比赛中甲所在队、丙所在队不能在同一场。先给甲选一个队友,但不能是丙的概率为
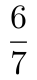
,再从组好的三支队伍中选一支除丙的队伍进行比赛,概率为
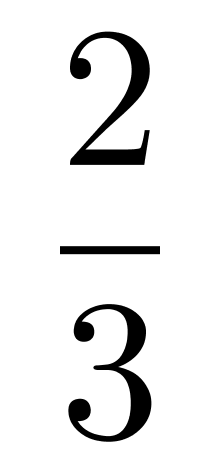
,则第一轮丙不与甲在同一场比赛的概率为
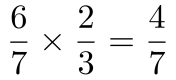
第三步,甲所在队第一轮获胜的概率为
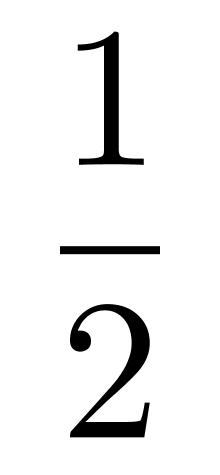
,丙所在队第一轮获胜的概率为
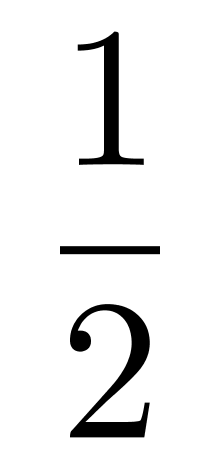
,甲所在队在决赛战胜丙所在队的概率为
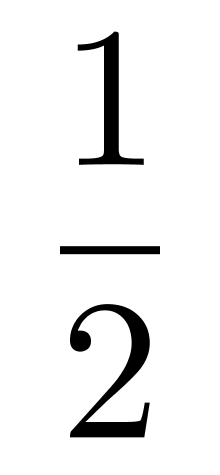
第四步,计算出总概率为
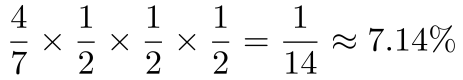
-
第3题:
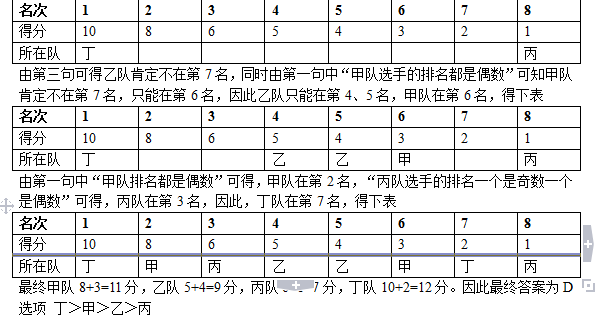
某市举办了一场职业技能竞赛有甲、乙、丙、丁四支代表队进入决赛每支队伍有两名参赛选手获得第一名的选手将得10分第二名得8分第三名到第八名分别是6、5、4、3、2、1分最后总分最高的队伍将获得冠军。比赛的排名情况如下
甲队选手的排名都是偶数乙队两名选手的排名相连丙队选手的排名一个是奇数一个是偶数丁队选手的排名都是奇数
?第一名是丁队选手第八名是丙队选手
?乙队两名选手的排名在甲队两名选手之间同时也在丙队两名选手之间。
根据以上条件可以判断各队总分由高到低的排列顺序为A. 丁>甲>丙>乙
B. 甲>丁>乙>丙
C. 甲>丁>丙>乙
D. 丁>甲>乙>丙答案:D解析:根据题干中信息列出下表,由将第2句填入得下表
-
第4题:
某单位派甲、乙两名选手组队参加乒乓球比赛,其中甲每场比赛均有40%的可能性获胜,乙每场比赛均有70%的可能性获胜。现安排甲参加1场比赛,乙参加2场比赛,总计获胜2场及以上即可出线。问该单位代表队出线的概率为:A.48.8%
B.56.4%
C.61.4%
D.65.8%答案:D解析:本题考查概率问题。
此题我们可以从反面求解,求该单位代表队出线的概率,即求获胜2场及以上的概率,我们从反面考虑,用1减去胜1场或0场的概率即可。
①甲乙3场都输的概率为:0.6×0.3×0.3=0.054;
②甲输1场,乙赢1场的概率为:0.6×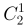 ×0.7×0.3=0.252;
×0.7×0.3=0.252;
③甲赢1场,乙输2场的概率为:0.4×0.3×0.3=0.036;
故所求概率为:1-0.054-0.252-0.036=0.658。
因此,选择D选项。 -
第5题:
甲和乙进行打靶比赛,各打两发子弹,中靶数量多的人获胜。甲每发子弹中靶的概率是60%,而乙每发子弹中靶的概率是30%。则比赛中乙战胜甲的可能性为:
A小于5%
B在5%~10%之间
C在10%~15%之间
D大于15%答案:C解析:
-
第6题:
甲、乙两人进行五子棋比赛,必须要经过A、B、C三场比赛的角逐,甲对乙每局获胜的概率 为60%,乙对甲每局获胜的概率为40%,则甲胜出的可能性为( )。
A.小于15%
B.介于15%--40%内
C.介于40%--60%内
D.大于60%答案:D解析:本题考查了分步计数原理和分类计数原理。甲胜出的可能情况有两种: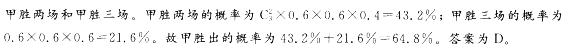
-
第7题:
网球比赛中,抽签获胜者可以选择场地。
正确答案:错误 -
第8题:
已知:(1)若甲和乙都参加比赛,则丙不能参加比赛。(2)只有乙参加比赛,丁才参加比赛。(3)甲和丙都参加了比赛。若以上判断都是真的,可否定乙和丁是否参加了比赛?写出推理过程。
正确答案: 由题目得知如下三个判断:
①、甲并且乙则非丙;②、只有乙,才丁;③、甲,并且丙;由此可作如下推理:(1)假设乙参加比赛,而根据判断③甲也参加比赛,按判断①可得出丙没有参加比赛,结论与判断③矛盾,可见,乙参加比赛不能成立。(2)由于乙没参加比赛,据判断②,则乙也不可能参加比赛,所以,乙和丁都没参加比赛。 -
第9题:
甲和乙进行打靶比赛,各打两发子弹,中靶数量多的人获胜。甲每发子弹中靶的概率是60%,而乙每发子弹中靶的概率是30%。则比赛中乙战胜甲的可能性()
- A、小于5%
- B、在5%~12%之间
- C、在10%~15%之间
- D、大于15%
正确答案:C -
第10题:
判断题网球比赛中,抽签获胜者可以选择场地。A对
B错
正确答案: 错解析: 暂无解析 -
第11题:
单选题跳跳镇上举行的跳跳舞比赛,最终获胜的冠军是()。A吟痴老人
B去年的获胜者
C乌丢丢
正确答案: A解析: 暂无解析 -
第12题:
小王、小张、小赵、小刘四人讨论比赛四强的甲、乙、丙、丁四个队伍哪个将获得冠军。
小王:“乙是冠军。”
小张:“冠军是丁或丙。”
小赵:“冠军是甲或丁。”
小刘:“甲和丙不是冠军。”
结果出来后,只有两个人的推断是正确的,冠军是:A.甲
B.乙
C.丙
D.丁答案:B解析:真假推理,题干提出有两个人为真,而冠军只有一个,本题可用假设法,假设小王推断正确,得出乙是冠军,同时小张“冠军是丁或丙”和小赵“冠军是甲或丁”推断不正确,小刘“甲和丙不是冠军”推断正确,符合题意,假设正确,得出冠军为乙,正确答案为B。 -
第13题:
甲、乙、丙三人打羽毛球,甲对乙、乙对丙和甲对丙的胜率分别为60%、50%和70%。比赛第一场甲与乙对阵,往后每场都由上一场的胜者对阵上一场的轮空者。则第三场比赛为甲对丙的概率比第二场( )。A. 低40个百分点
B. 低20个百分点
C. 高40个百分点
D. 高20个百分点答案:A解析:如果甲和丙在第二场比赛中相遇,则对阵方式为,甲乙第一场,甲晋级,概率为60%;如果甲和丙在第三场比赛中相遇,则对阵方式为甲乙打第一场比赛,乙晋级,然后与轮空的丙打第二场比赛,丙晋级,与轮空的甲打第三场比赛,所以概率为40%×50%=20%,20%-60%=-40%。所以选择A。 -
第14题:
乒乓球队员甲、乙技术水平相当,为一决胜负,他俩需进行五局比赛,规定五局三胜者为胜。已知前两局比赛甲获胜,这时乙最终获胜的概率是: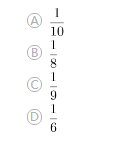 答案:B解析:第一步,本题考查概率问题,属于分类分步型。
答案:B解析:第一步,本题考查概率问题,属于分类分步型。
第二步,甲、乙技术水平相当,可知在每局比赛中二人胜出的概率均为1/2,乙想要最终获胜,则后三局乙均获胜。故所求概率为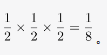
-
第15题:
甲、乙、丙、丁4个足球队参加比赛,假设每场比赛各队取胜的概率相等,现任意将这4个队分成两个组(每组两个队)进行比赛,胜者再赛,则甲、乙相遇的概率为( )A.1/6
B.1/4
C.1/5
D.1/3
E.1/2答案:E解析:
-
第16题:
甲和乙进行5局3胜的乒乓球比赛,甲每局获胜的概率是乙每局获胜概率的1.5倍。问以下哪种情况发生的概率最大?A.比赛在3局内结束
B.乙连胜3局获胜
C.甲获胜且两人均无连胜
D.乙用4局获胜答案:A解析:第一步,本题考查概率问题。
第二步,根据甲获胜的概率是乙获胜概率的1.5倍,令乙获胜的概率为2x,则甲为3x,又甲获胜的概率和乙获胜的概率总和为1,可列式2x+3x=1,解得x=20%,则乙获胜的概率为40%,甲获胜的概率为60%。
第三步,选项信息充分,采用代入排除法解题。
代入A选项,比赛在3局内结束,则情况为甲前3局获胜或乙前3局获胜,概率为
(60%)^3+(40%)^3;
代入B选项,乙连胜3局获胜,情况有三种:乙前3局连胜、乙第一局输后面的三局连胜、乙前两局输后面的三局连胜,概率为(40%)^3+60%×(40%)^3+60%×60%×(40%)3;
代入C选项,甲获胜且两人均无连胜,则情况只有一种:甲胜乙胜甲胜乙胜甲胜,概率为60%×40%×60%×40%×60%;
代入D选项,乙用4局获胜,则情况为前3局乙胜2局,最后一局为乙胜,概率为;
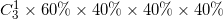
AB选项计算方式接近,优先进行比较:
(60%)^3+(40%)^3>60%×(40%)^3+60%×60%×(40%)3,排除B选项。
CD选项计算方式接近,优先进行比较。D选项数据>C选项数据,排除C选项。
AD比较,(60%)^3+(40%)^3>
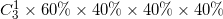
-
第17题:
2004年奥运会网球比赛中,中国女子双打选手获得冠军是()。
正确答案:孙甜甜、李婷 -
第18题:
跳跳镇上举行的跳跳舞比赛,最终获胜的冠军是()。
- A、吟痴老人
- B、去年的获胜者
- C、乌丢丢
正确答案:C -
第19题:
()是指将所有参赛选手编排成一定的比赛次序,相邻的两名选手进行比赛,败者被淘汰,胜者进入下一轮,直至整个比赛最后一场的胜者为冠军,负者为亚军。
- A、循环法
- B、顺序法
- C、单淘汰
- D、双淘汰
正确答案:C -
第20题:
单选题()是指将所有参赛选手编排成一定的比赛次序,相邻的两名选手进行比赛,败者被淘汰,胜者进入下一轮,直至整个比赛最后一场的胜者为冠军,负者为亚军。A循环法
B顺序法
C单淘汰
D双淘汰
正确答案: C解析: 暂无解析 -
第21题:
单选题某场羽毛球单打比赛采取三局两胜制。假设甲选手在每局都有80%的概率赢乙选手,那么这场单打比赛甲有多大的概率战胜乙选手:A0.768
B0.800
C0.896
D0.924
正确答案: B解析: -
第22题:
单选题甲和乙进行打靶比赛,各打两发子弹,中靶数量多的人获胜。甲每发子弹中靶的概率是60%,而乙每发子弹中靶的概率是30%。则比赛中乙战胜甲的可能性:A小于 5%
B在 5%~12%之间
C在 10%~15%之间
D大于 15%
正确答案: D解析:
