假定某门学科的测验成绩分布为正态分布，从某一学区随机抽取的65名考生的 平均分为74,标准差为8。 该学区所有考生平均成绩的99%的罝信区间是A.73.20-74.80 B.72.04-75.96 C.72.36-75.64 D.71.42-76.58

题目
假定某门学科的测验成绩分布为正态分布，从某一学区随机抽取的65名考生的 平均分为74,标准差为8。 该学区所有考生平均成绩的99%的罝信区间是

A.73.20-74.80
B.72.04-75.96
C.72.36-75.64
D.71.42-76.58
相似考题

1.老师出了若干份试卷，以各份试卷的平均分计算考生的成绩，某考生最后一份试卷得97分，则平均分为90分，若该考生最后一份试卷得73分，则平均分为87分，那么这组试卷的份数是（ ）。A．8B．9C．10 $_$D．11

2.老师出了若干份试卷，以各份试卷的平均分计算考生的成绩，某考生最后一份试卷得97分，则平均分为90分，若该考生最后一份试卷得73分，则平均分为87分，那么这组试卷的份数是( )。A．8B．9C．10D．11

3.在一次考试中，所有考生平均成绩为75分，其中男考生人数比女考生多80%，而女考生平均成绩比男考生高20%，则女考生平均成绩为（ ）分。A．83B．84C．85D．86

4.抽样调查表明，考生的外语成绩(百分制)近似服从正态分布，平均成绩72分，已知90分以上的考生占2.3%，试求考生成绩在63至81分之间的概率。

更多“假定某门学科的测验成绩分布为正态分布，从某一学区随机抽取的65名考生的 平均分为74,标准差为8。 该学区所有考生平均成绩的99%的罝信区间是”相关问题

  • 第1题：

    老师出了若干份试卷，以各份试卷的平均分计算考生的成绩，若某考生最后一份试卷得97分，则平均分为90分，若该考生最后一份试卷得73分，则平均分为87，分，那么这组试卷有多少份?（ ） A．8 B．9 C．10 D．11


    正确答案：A
    由题意可知，该考生最后一份试卷得97分与得73分其总分相差97—73=24分，平均分相差90—87=3分，则这组试卷有24÷3=8份。故选A。

  • 第2题：

    某次百分制考试共有30名考生参加，每人的成绩均为正整数，所有考生平均成绩为80分，且所有考生成绩均不相同。问成绩低于60分的考生最多有多少人

    A.7
    B.8
    C.9
    D.10

    答案：B
    解析：
    第一步，30人成绩互不相同，且为整数，使用枚举法。第二步，高分越高，低于60分的分数也越高，则低于60分的考生人数会越多，平均数是80分，本题采用中位数法计算，取中位数为80。第三步，81分至100分共计20个分数，则高出80分的分差和为1＋2＋……＋20＝210分，低于60分的分数，最高为59分，假设剩余的10个分数均低于60分，则低于80分的分差和最多为21＋22＋……＋30＝255分，210小于255分，10人不可能。第四步，若9个分数低于60分，则低于80分的分差和最多为255－30＝225，225大于210，9人也不可能。第五步，若8个分数低于60分，则低于80分的分差和最多为255－30－29＝196,196小于210,8人低于60分，没问题，只需另外2个人的低于80分的分差和为14即可。因此，选择B选项。

  • 第3题：

    对某中学初中一年级学生实施了标准化的数学考试，全体学生成绩的平均分为83分，某一学生得了80分，他数学成绩的z值为-0.5，问全体考生数学成绩的标准差为()

    A.12
    B.6
    C.8
    D.10

    答案：B
    解析：
    描述统计；相对量数；标准分数。 用Z分数的定义公式就能算出来，标准差是6。

  • 第4题：

    已知某市高三学生的数学平均成绩为85分，从某校随机抽取28名高三学生，其数学测验的平均成绩为87.5分，标准差为10分，该校高三学生的数学成绩与全市高三学生的数学成绩的关系是()

    A.差异显著
    B.该校学生的数学成绩高于全市
    C.差异不显著
    D.该校学生的数学成绩低于全市

    答案：C
    解析：
    推断统计；假设检验。 题目为样本与总体平均数差异的检验。其中，总体正态分布，总体方差未知，应进行f检验。

  • 第5题：

    当从一万个高考生的成绩中（正态分布）随机抽取容量为1 000的样本时，其样本方差与总：体方差的比值分布是()分布。

    A.T分布
    B.Z分布
    C.F分布
    D.X2分布

    答案：D
    解析：
    推断统计；假设检验。 当从正态分布的总体中随机抽取容量为n的样本时，其方差与总体方差的比值分布是卡方分布。

  • 第6题：

    已知某次高考的数学成绩服从正态分布，从这个总体中随即抽取n=37的样本，并计算得其平均分为79分，标准差为9分。那么下列成绩不在这次考试中全体考生成绩均值μ的0．95置信区间之内的是（　　）

    A.77
    B.80
    C.81
    D.85

    答案：D
    解析：
    本题旨在考查考生对区间估计知识点的掌握程度。根据题意可知，本题属于“总体方差未知时，用样本的无偏方差作为总体方差的估计值，实现对总体平均数μ的估计”的情况。且总体分布为正态分布，因此总体均值的置信区间为{img src="/main/97/u/2011040805490657152}frac{S}{sqrt{n-1}}" align='absmiddle'/} ，同时95％的概率推测即z=1．96。将题目中的已知量代入公式即 ，也即73.1＜μ＜84.9。故本题的正确答案是D。

  • 第7题：

    有300名考生，期中和期末考试成绩的相关系数为0.62，两次考试成绩平均分数均为80分。如果给所有考生的期中成绩各加8分，加分后两次成绩的相关系数是

    A.0.52
    B.0.62
    C.0.70
    D.0.72

    答案：B
    解析：
    本题中的相关系数是两列连续变量的相关系数，是积差相关系数，公式为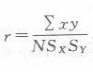

    其中x、y为两个变量的离均差，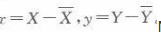

    N是成对数据的数目。SX是X变量的标准差。SY是y变量的标准差。在本题中，每个数值都加8，即每个变量的平均数也加8，即两个变量的离均差没有变化，根据标准差的公式是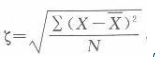

    可得两个变量的标准差也没有变化，即相关系数就也没有变化。

  • 第8题：

    假定某门学科的测验成绩分布为正态分布，从某一学区随机抽取的65名考生的 平均分为74,标准差为8。 在其他有关条件保持不变的情况下，下列叙述正确的是

    A.置信区间值越大，置信区间范围越宽
    B.罝信区间值变小，罝信区间范围不变
    C.显著性水平值越大，罝信区间范围越宽
    D.显著性水平值越小，S信区间范围越窄

    答案：A
    解析：
    考査影响置信区间的因素，罝信水平越大，显著性α值越小，Z值越大，区间越宽。

  • 第9题：

    某学校统计学考试成绩服从正态分布，以往经验表明成绩的标准差为10分。从学生中随机抽取25个简单随机样本，他们的平均分数是84.32分。根据这些数据计算该校学生的统计学考试的平均成绩的95%的置信区间是（）

    • A、84.32±39.2
    • B、84.32±1.96
    • C、84.32±3.92
    • D、84.32±19.6

    正确答案:C

  • 第10题：

    某次考试中，成绩不超过30分的有153名考生，平均分为24分；成绩不低于80分的有59名考生，平均分为92分；成绩超过30分的平均分为62分；成绩低于80分的平均分为54分。那么参加这次考试的考生共有（）人。

    • A、795
    • B、875
    • C、1007
    • D、1264

    正确答案:C

  • 第11题：

    填空题
    设某地区高考成绩服从平均数为550，标准差为100的正态分布，随机抽取50人，以95.45%的概率保证程度估计该地区高考平均分数的区间在（）分

    正确答案： 521.72——578.28
    解析： 暂无解析

  • 第12题：

    单选题
    某学校统计学考试成绩服从正态分布，以往经验表明成绩的标准差为10分。从学生中随机抽取25个简单随机样本，他们的平均分数是84.32分。根据这些数据计算该校学生的统计学考试的平均成绩的95%的置信区间是（）
    A

    84.32±39.2

    B

    84.32±1.96

    C

    84.32±3.92

    D

    84.32±19.6


    正确答案： A
    解析： 暂无解析

  • 第13题：

    老师出了若干份试卷，以各份试卷的平均分计算考生的成绩，某考生最后一份试卷得97分，则均分为90分，若该考生试卷得73分，则平均分为87分，那么这组试卷的份数是？


    A. 8
    B. 9
    C. 10
    D. 11

    答案：A
    解析：
    解题指导： 设这组试卷x份。 90x-97=87x-73 3x=24 x=8。故答案为A。

  • 第14题：

    设某次考试的学生成绩服从正态分布，从中随机地抽取36位考生的成绩，算得平均成绩为66.5分，标准差为15分，问在显著性水平为0.05下，是否可以认为这次考试全体考生的平均成绩为70分？并给出检验过程.
    　　附表：t分布表


    答案：
    解析：
    【详解】设该次考试的考生成绩为X，则X～N(μ，σ^2).把从X中抽取的容量为n的样本均值记为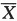，样本标准差记为S.本题就是要在显著性水平α=0.05下检验假设H0：μ=70；H1：μ≠70.
    由于σ^2未知，故用t检验，选用检验统计量.T=现在μ0=70，n=36.
    拒绝域为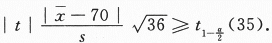
    由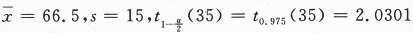，算得

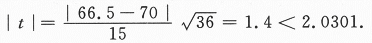
    所以接受假设H0：μ=70，即在显著水平0.05下，可以认为这次考试全体考生的平均成绩为70分.

  • 第15题：

    某年高考理科数学全国平均成绩为97分，标准差是11.5分，某考生数学成绩为120分，求他的标准分数是多少？()

    A.1
    B.2
    C.3
    D.4

    答案：B
    解析：
    描述统计；相对量数；标准分数。 Z分数可以用来表示某一分数在团体中的相对位置。虽然百分等级也可以进行分数相对位置的比较，但根据选项条件可知，本题应选择Z分数进行比较。已知数学平均成绩为97分，标准差是11.5分，考生数学成绩为120分，

  • 第16题：

    某班级一次英语考试成绩服从正态分布，其全班成绩平均分为65分，标准差为5分，请问分数在60到70之间的人数占全体考生的百分比为()

    A.15. 8%
    B.34. 1%
    C.50. 0%
    D.68. 3%

    答案：D
    解析：
    推断统计；推断统计的数学基础。将原始分数的区间转化为Z分数的区间，因为60 ＜X＜70，所以(60 -65)/5 ＜Z＜ (70- 65)/5，得到-1 ＜Z＜ +1。由标准正态分布的性质可知±1个标准差之间包含所有数据的68. 26%。

  • 第17题：

    表3—1是2006年中国31个主要城市年平均相对湿度的数据(单位：%)。



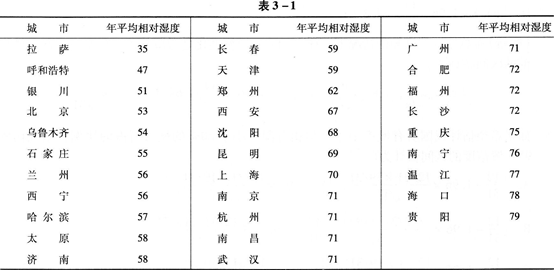
    31个城市的年平均相对湿度可以视为从全国所有城市中抽取的随机样本。假定全国年平均相对湿度服从正态分布，且总体标准差为11，则全国年平均相对湿度95%置信度的区间估计为（ ）。



    答案：A
    解析：
    在总体方差已知的情况下，样本均值经过标准化之后服从正态分布，因此总体均值的区间估计为：

  • 第18题：

    在某学校的一次考试中，已知全体学生的成绩服从正态分布，其总方差为100。从中抽取25名学生，其平均成绩为80，方差为64。以99%的置信度估计该学校全体学生成绩均值的置信区间是

    A.[76.08,83.92]
    B.[75.90,84.10]
    C.[76.86,83.14]
    D.[74.84,85.16]

    答案：D
    解析：

  • 第19题：

    假定某门学科的测验成绩分布为正态分布，从某一学区随机抽取的65名考生的 平均分为74,标准差为8。 根据本次测验成绩，该测验分数的平均数的标准误


    答案：A
    解析：
    题考察的是标准误的计算公式，总体正态，方差未知，则标准为

  • 第20题：

    某超市想要估平均金额，采取简单随机方式抽取49名顾客进行调查。假定从正态分布，且标准差为15元。如果样本均值为120元求总体均值95%的置信区间。

    略

  • 第21题：

    假设某班期末统计学考试成绩服从正态分布，平均成绩为70分，标准差为12分，要求计算： （1）随机抽取1人，该同学成绩在82分以上的概率； （2）随机抽取9人，其平均成绩在82分以上的概率。


    正确答案:（1）15.86%, (2)0.135%

  • 第22题：

    设某地区高考成绩服从平均数为550，标准差为100的正态分布，随机抽取50人，以95.45%的概率保证程度估计该地区高考平均分数的区间在（）分


    正确答案:521.72——578.28

  • 第23题：

    多选题
    已知某次物理考试非正态分布，σ=8，从这个总体中随机抽取n=64的样本，并计算得其平均分为71，那么下列成绩在这次考试中全体考生成绩均值μ的0.95的置信区间之内的有（）
    A

    69

    B

    70

    C

    71

    D

    72


    正确答案： B,D
    解析： 暂无解析

相关内容