若函数z=z(x，y)由方程确定，则=_________.
题目
确定，则
=_________.相似考题
更多“若函数z=z(x，y)由方程确定，则=_________.”相关问题
-
第1题：
下面关于函数依赖的叙述中，不正确的是
A．若X→Y，Y→Z，则X→Z
B．若X→y，且Y→CY，则X→Y，
C．若X→Y，X--Z，则X→YZ
D．若XY→Z，则X→Z，Y→Z
正确答案：D
解析：若有XY→Z，“X→Z，Y→Z”可能都不成立，但当“X→Z，Y→Z”成立时，可以有“XY→Z”。 -
第2题：
下面关于函数依赖的叙述中，不正确的是——。
A．若X→Y，Y→Z，则X→YZ
B．若X→Y，Y→Z，则X→Z
C．若Z→Y，Y’是Y的子集，则X→Y
D．若XY→Z．则X→Z．Y→Z
正确答案：D
解析：函数依赖公理：设有关系模式R(u．F)，u为属性全集，F是R的一组函数依赖，X、Y、z是U的子集。
1)自反律若x包含Y，则有x—Y
2)增广律若x—Y，则有XZ—YZ
3)传递律若x—Y，Y—z。则有x—z
推论1 若x—Y，x—z，则有x一YZ
推论2若x—Y且z是Y的子集，则有x-z
推论3若x—Y，YZ—w，则有XZ—W
若x—Y，Y—z，由传递律，则x—z。B项正确。
若x—Y，Y—z，则x—z，又x—Y，由推论l。则x—YZ。A项正确。若x—Y，Y’是Y的子集，由推论2，则x—Y。C项正确。若XY—z，则x-Z，Y也-斗Z。所以D项不正确。 -
第3题：
下面关于函数依赖的叙述中，不正确的是（ ）。
A)若XY→Z，则X→Z，Y→Z
B)若X→Y，X→Z，则X→YZ
C)若X→Y，则XZ→YZ
D)若X→Y，WY→Z，则XW→Z
正确答案：A
函数依赖：若R(U)的任意一个可能的关系r，r中不可能存在两个元组在X上的属性值相等，而在Y上的属性值不等，则称“X函数确定Y”，或“Y函数依赖X”。 -
第4题：
(本题满分8分) 设函数z=z(x，y)是由方程x+y3+z+e2x=1所确定的隐函数，求dz．
正确答案：
-
第5题：
下面关于函数依赖的叙述中，不正确的是
A． 若X→Y，Y→Z，则X→Z
B．若X→Y，且
，则X→Y’C．若X→Y，X→Z，则X→YZ
D．若XY→Z，则X→Z，Y→Z
正确答案：D
解析：选项A为传递律，选项B为分解规则，选项C为合并规则，而合并规则不是可逆的，所以选项D不正确，即为本题的答案。 -
第6题：
下面关于函数依赖的叙述中，不正确的是
A．若X→Y，X→Z，则X→YZ
B．若Z→XY，则Z→X，Z→Y
C．若X→Y，Y∈Z，则X→Z
D．若Y'∈Y，Y’→X，则Y→X
正确答案：C
解析：根据函数依赖的合并规则、传递规则和分解规则可证明选项ABD是正确的。 -
第7题：
下列关于函数依赖性不正确的是( )。
A．若X→Y，X→Z，则X→YZ
B．若XY→Z，则X→Z，Y→Z
C．若X→Y，WY→Z，则XW→Z
D．若X→Y，Y→Z，则X→Z
正确答案：B
解析：Armstrong公理系统中，选项A属于合并规则，选项C属于伪传递规则，选项D属于传递规则，合并规则的逆并不一定成立。 -
第8题：
设z=z(x，y)是由方程x2+y2+z2=ez所确定的隐函数，求dz．答案：解析：
-
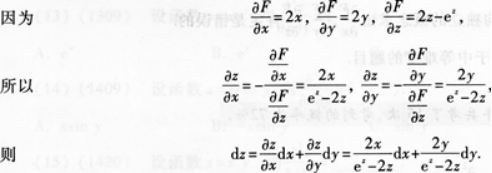
第9题：
设Z=Z(x，Y)是由方程x+y3+z+e2=1确定的函数，求dz答案：解析：利用隐函数求偏导数公式，记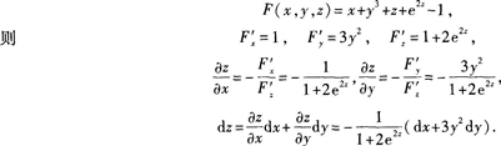
-
第10题：
单选题设函数z＝z（x，y）由方程z＝e2x－3z＋2y确定，则3∂z/∂x＋（∂z/∂y）＝（ ）。A2
B1
Ce
D0
正确答案： A解析：
构造函数F（x，y，z）＝z－e2x－3z－2y。则∂z/∂x＝－Fx′/Fz′＝2e2x－3z/（1＋3e2x－3z），∂z/∂y＝－Fy′/Fz′＝2/（1＋3e2x－3z），故3∂z/∂x＋（∂z/∂y）＝2。 -
第11题：
单选题设函数z＝z（x，y）由方程z＝e2x－3z＋2y确定，则3∂z/∂x＋（∂z/∂y）＝（ ）。A0
B1
C2
D4
正确答案： B解析：
构造函数F（x，y，z）＝z－e2x－3z－2y。则∂z/∂x＝－Fx′/Fz′＝2e2x－3z/（1＋3e2x－3z），∂z/∂y＝－Fy′/Fz′＝2/（1＋3e2x－3z），故3∂z/∂x＋（∂z/∂y）＝2。 -
第12题：
单选题由方程f（y/x，z/x）＝0确定z＝z（x，y）（f可微），则x∂z/∂x＋y∂z/∂y＝（ ）。A－z
Bz
C－y
Dy
正确答案： C解析：
由f（y/x，z/x）＝0可得，∂z/∂x＝－[f1′·（－y/x2）＋f2′·（－z/x2）]/（f2′/x），∂z/∂y＝－（f1′/x）/（f2′/x），则x∂z/∂x＋y∂z/∂y＝－（―yf1′/x―zf2′/x＋yf1′/x）/（f2′/x）＝z。 -
第13题：
下面关系函数依赖的传述中，不正确的是______。
A) 若XY——>Z，则X——>Z，Y——>Z
B) 若X——>Y，Y——>Z，则X——>YZ
C) 若X——>Y，Z包含Y，则X——>Z
D) 若X——>Y，Y——>Z，则X——>Z
正确答案：A
(4) [解析] 由数据依赖的公理系统可知，函数依赖关系必须满足自反律、增广律、传递律(即选项D)，这三点又可推出函数依赖具有合并律(即选项 B)，伪传递规则和分解规则(即选项C)，A是不成立的。
[答案] A
-
第14题：
下面关于函数依赖的叙述中，不正确的是（ ）。
A)若X→Y，Y→Z，则X→YZ
B)若X→Y，Y’包含Y，则X→Y'
C)若X→Y，Y→Z，则X→Z
D)若XY→Z，则X→Z，Y→Z
正确答案：D
设R(U)是属性集U上的关系模式，X， Y，Z是U的子集。若对R(U)的任意一个可能的关系r，r中不可能存在两个元组在x上的属性值相等，而在Y上属性值不等，则称“X函数确定Y”或“Y函数依赖于X”，记作X—Y，X称为决定因素。
根据Armstrong公理系统的三条定律.可以知道:
根据合并律可知选项A)正确；
根据增广律可知选项B)正确；
根据传递律可知选项C)正确。 -
第15题：
下列关于部分函数依赖的叙述中，哪一条是正确的？
A．若X→Y，且存在属性集Z，Z∩Y≠￠,X→Z，则称Y对X部分函数依赖
B．若X→Y，且存在属性集Z，Z∩Y=￠，X→Z，则称Y对X部分函数依赖
C．若X→Y，且存在X的真子集X’Z，X’→Z，则称Y对X部分函数依赖
D．若X→Y，且对于X的任何真子集X’，都有
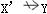，则称Y对X部分函数依赖正确答案：C
解析：在关系模式R中,如果X→Y,且对于X的任何一个真子集X',都有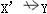
，则称Y对完全函数依赖；若X→Y，但Y不完全函数依赖于X，称Y对X部分函数依赖。
-
第16题：
下面关于函数依赖的叙述中，不正确的是( )。
A．若X→Y，Y→Z，则X→Z
B．若X→Y，
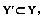，则X→Y'C．若X→Y，X→Z，则X→YZ
D．若XY→Z，则X→Z，Y→Z
正确答案：D
解析：本题考查函数依赖的公理系统。选项A为传递律，选项B为分解规则，选项C为合并规则，而合并规则不是可逆的，所以选项D不正确，即为本题的答案。 -
第17题：
下面关于函数依赖的叙述中,不正确的是
A．若X→Y,Y→Z,则X→Z
B．若X→Y,且Y′ Y,则X→Y′
C．若X→Y,X→Z,则X→YZ
D．若XY→Z,则X→Z,Y→Z
正确答案：D
解析：选项A为传递律,选项B为分解规则,选项C为合并规则,而合并规则不是可逆的,所以选项D不正确,即为本题的答案。 -
第18题：
下面关于函数依赖的叙述中，错误的是_________。
A．若X→Y，Y→Z，则X→YZ
B．若XY→Z，则X→Y，Y→Z
C．若X→Y，WY→Z，则XW→Z
D．若X→Y 及Z包含于Y，则X→Z
正确答案：B
解析：1、合并规则：由X→Y，X→Z，有X→YZ。2、伪传递规则：由X→Y，WY→Z，有XW→Z。3、分解规则：由X→Y，及Z包含于Y，有X→Z。 -
第19题：
下面关于函数依赖的叙述中，正确的是（ ）。
Ⅰ.若X→Y，X→Z，则X→YZⅡ.若XY→Z，则x→Z，Y→Z
Ⅲ.若X→Y，WY→Z，则X→ZⅣ.若X→Y，Y→Y’，则X→Y’
正确答案：B
根据函数依赖的几个概念和Armstrong公理系统的推理规则来逐个判断。 -
第20题：
设函数z=z(x，y)由方程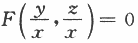
确定，其中F为可微函数，且F'2≠0，则
=A.Ax
B.z
C.-x
D.-z答案：B解析：
-
第21题：
问答题求由方程x2＋y2＋z2－xz－yz－2x－2y＋2z－6＝0确定的函数z＝z（x，y）的极值。正确答案：
先求出函数z的各个偏导:
由原方程可得,原方程两边对x求导得
2x+2z·zx′-z-(x+y)zx′-2+2zx′=0①
原方程两边对y求导得
2y+2z·zy′-z-(x+y)zy′-2+2zy′=0②
①②中,令zx′=0,zy′=0,解得x=(z+2)/2,y=(z+2)/2,将其代入已知方程得Z=±4,故驻点为(3,3)和(-1,-1)。
①式两边对x,y分别求导得
2+2(zx′)2+2zzxx″-2zx′+(2-x-y)zxx″=0③
2zy′zx′+2zzxy″-zy′-zx′+(2-x-y)zxy″=0④
②式两边对y求导得
2+2(zy′)2+2zzyy″-2zy′+(2-x-y)zyy″=0⑤
当x=y=-1,z=-4时,zx′=zy′=0,将其代入③④⑤,得A=zxx″(-1,-1)=1/2,B=zxy″(-1,-1)=0,C=zyy″(-1,-1)=1/2,B2-AC=-1/4<0,A=1/2>0。
则函数z在(-1,-1)处取得极小值z=-4。
当x=y=3,z=4时,zx′=zy′=0,并将其代入③④⑤,得A=zxx″(3,3)=-1/2,B=zxy″(3,3)=0,C=zyy″(3,3)=-1/2,B2-AC=-1/4<0,A=-1/2<0。
故z在(3,3)点处取到极大值z=4。解析： 暂无解析 -
第22题：
填空题设函数z＝z（x，y）由方程z＝e2x－3z＋2y确定，则3∂z/∂x＋∂z/∂y＝____。正确答案： 2解析：
方程两边同时对x求偏导，则∂z/∂x＝e2x－3z（2－3∂z/∂x），可得∂z/∂x＝2e2x－3z/（1＋3e2x－3z）。同理∂z/∂y＝e2x－3z（－3∂z/∂y）＋2，可得∂z/∂y＝2/（1＋3e2x－3z），所以3∂z/∂x＋∂z/∂y＝6e2x－3z/（1＋3e2x－3z）＋2/（1＋3e2x－3z）＝2（1＋3e2x－3z）/（1＋3e2x－3z）＝2。 -
第23题：
填空题设函数z＝z（x，y）由方程F（x－az，y－bz）＝0所给出，其中F（u，v）任意可微，则a∂z/∂x＋（b∂z/∂y）＝____。正确答案： 1解析：
根据偏导数的求解方法可知∂z/∂x＝－Fx′/Fz′＝－F1′/（―aF1′―bF2′），∂z/∂y＝－Fy′/Fz′＝－F2′/（―aF1′―bF2′），故a∂z/∂x＋（b∂z/∂y）＝－（aF1′＋bF2′）/（―aF1′―bF2′）＝1。