用克拉默法则解线性方程组

题目
用克拉默法则解线性方程组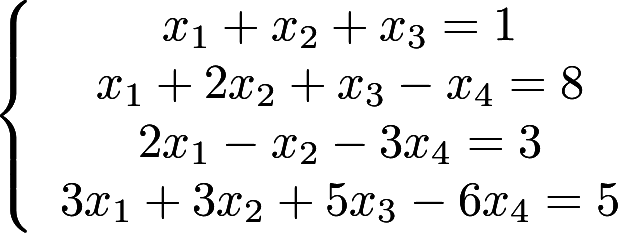

相似考题

1.设n元齐次线性方程组AX=O只有零解,则秩(A)=()。

2.用迭代法解线性方程组时，迭代能否收敛与初始向量的选择、系数矩阵及其演变方式有关，与常数项无关。()

3.非齐次线性方程组任意两个解之差为对应系数的齐次线性方程组的解。()

4.若r(A,b)=4,r(A)=3,则线性方程组AX=b解的情况是()。

更多“用克拉默法则解线性方程组”相关问题

  • 第1题：

    用高斯顺序消去法解线性方程组，消元能进行到底的充分必要条件是线性方程组的系数矩阵的各阶顺序主子式均不为0()


    参考答案：√

  • 第2题：

    设A为矩阵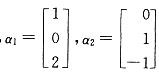，都是线性方程组Ax=0的解，则矩阵A为：


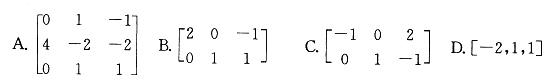    答案：D
    解析：
    提示：a1，a2是方程组Ax=0的两个线性无关的解，方程组含有3个未知量，帮矩阵A的秩R（A）=3-2=1，而选项A、B、C的秩分别为3、2、2，均不符合要求。将选项D代入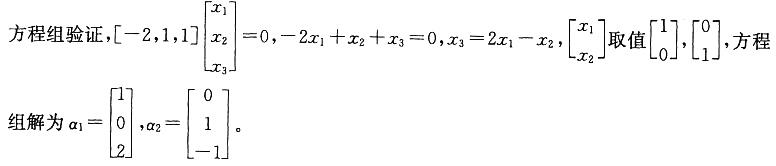

  • 第3题：

    给定线性方程组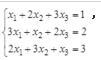

    则其解的情况正确的是（　　）。

    A．有无穷多个解
    B．有唯一解
    C．有多于1个的有限个解
    D．无解

    答案：B
    解析：

  • 第4题：

    解线性方程组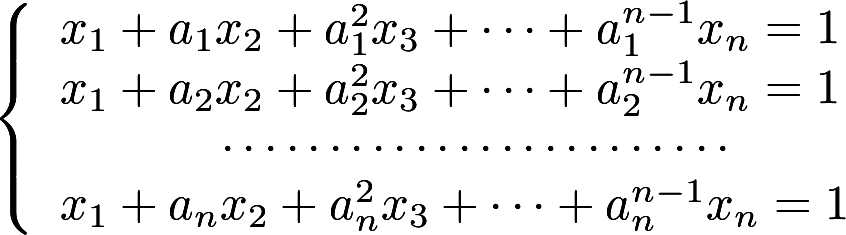其中 .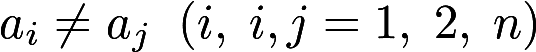


    答案：
    解析：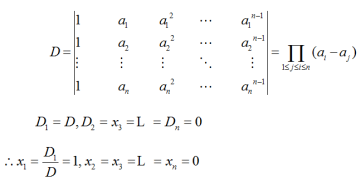

  • 第5题：

    求齐次线性方程组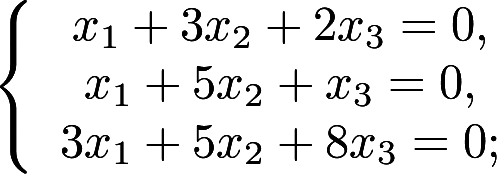的基础解系


    答案：
    解析：

  • 第6题：

    解非齐次线性方程组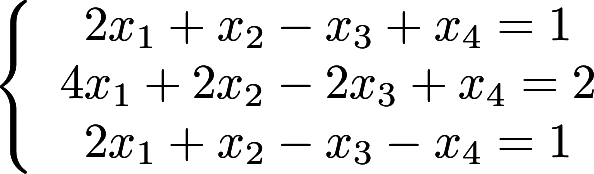


    答案：
    解析：

  • 第7题：

    已知下列非齐次线性方程组(Ⅰ)，(Ⅱ)
    　　
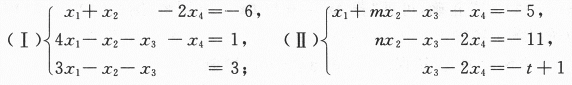
    　　(1)求解方程组(Ⅰ)，用其导出组的基础解系表示通解.
    　　(2)当方程组中的参数m，n，t为何值时，方程组(Ⅰ)与(Ⅱ)同解.


    答案：
    解析：

  • 第8题：

    设线性方程组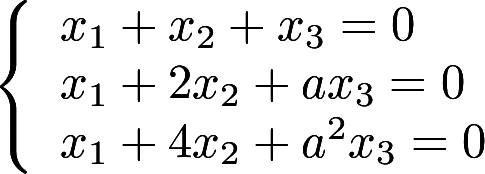与方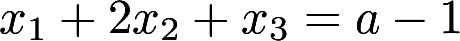程有公共解，求a的值及所有公共解


    答案：
    解析：

  • 第9题：

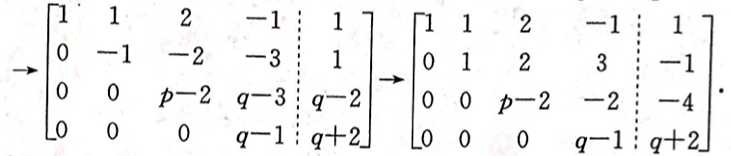
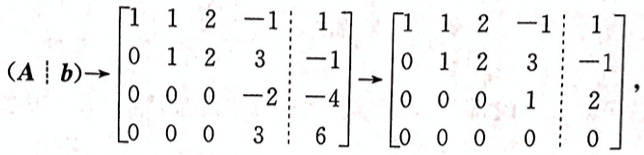
    设线性方程组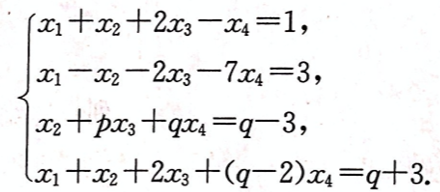问方程组何时无解，有唯一解，有无穷多解，有无穷多解时，求出其全部解。


    答案：
    解析：
    将方程组的增广矩阵作初等行变换，有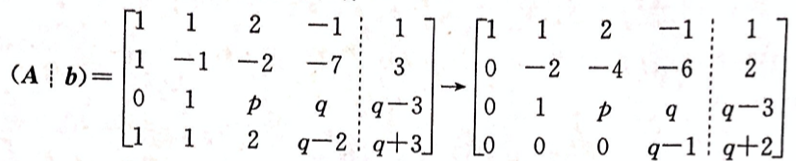

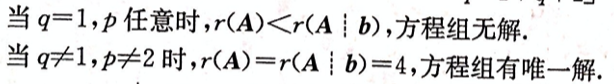
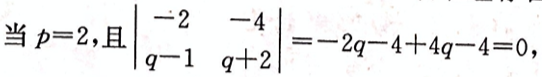
  • 第10题：

    求齐次线性方程组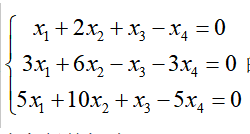的全部解（要求用基础解系表示）。


    答案：
    解析：
    解：本题考查齐次线性方程组的解法。

  • 第11题：

    单选题
    用列主元消去法解线性方程组 ，第1次消元，选择主元为（） 。
    A

    -4

    B

    3

    C

    4

    D

    -9


    正确答案： A
    解析： 暂无解析

  • 第12题：

    用列主元消去法解线性方程组,

    A、3

    B、4

    C、-4

    D、9


    参考答案：C

  • 第13题：

    齐次线性方程组AX=0若有两个不同的解，它就有无穷多个解


    答案：对
    解析：

  • 第14题：

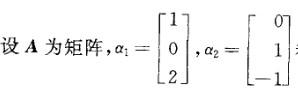    都是线性方程组Ax=0的解，则矩阵A为:


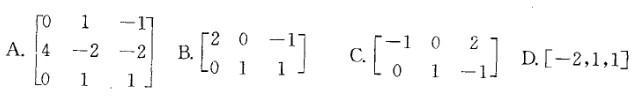    答案：D
    解析：
    提示:a1,a2是方程组Ax=0的两个线性无关的解，方程组含有3个未知量，故矩阵A的秩R(A)=3-2=1，而选项A、B、C的秩分别为3、2、2均不符合要求。将选项D代入方程组_

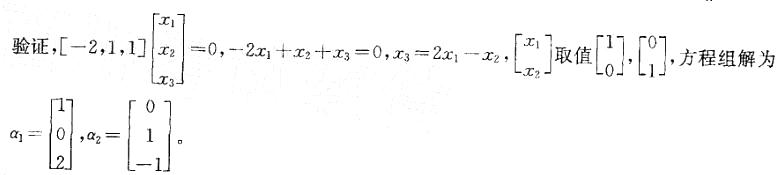  • 第15题：

    用克拉默法则解方程组


    答案：
    解析：

  • 第16题：

    解齐次线性方程组：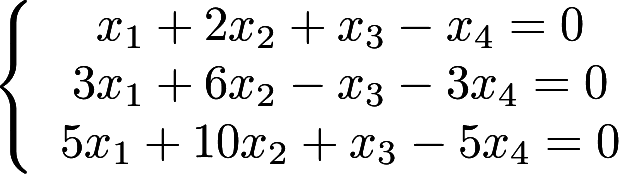


    答案：
    解析：

  • 第17题：

    已知齐次线性方程组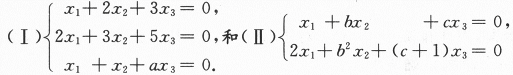
    同解，求a，b，c的值.


    答案：
    解析：

  • 第18题：

    求出一个齐次线性方程组，使它的基础解系由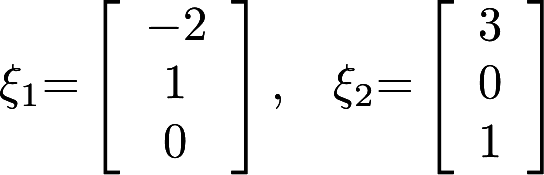向量组成


    答案：
    解析：

  • 第19题：

    设线性方程组(I)与(II)有公共的非零解,其中(I)为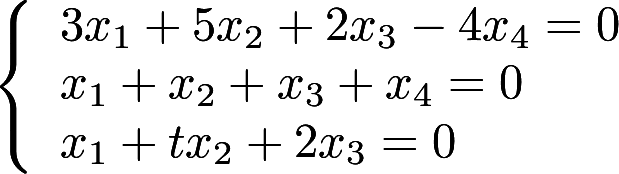，(II)有基础解系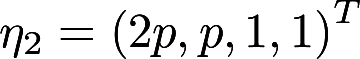，求p,t的值和全部公共解


    答案：
    解析：

  • 第20题：

    设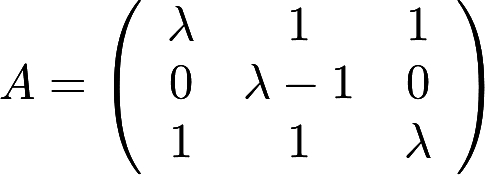，，已知线性方程组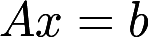存在两个不同的解.


    答案：
    解析：

  • 第21题：

    齐次线性方程组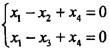的基础解系为（ ）。


    答案：C
    解析：
    提示：求解所给方程组，得基础解系α1=（1,1,1,0）T,α2=（-1,0,0,1）T,故选C。也可将选项代入方程验证。

相关内容