设总体X～N（0,σ^2）,X1,X2,…,X20是总体X的简单样本,求统计量U=所服从的分布.

题目
设总体X～N（0,σ^2）,X1,X2,…,X20是总体X的简单样本,求统计量U=所服从的分布.

相似考题

1.设X1，X2，…，X16是来自总体X~N(4，б2)的简单随机样本，б2已知，令，则统计量服从的概率密度函数为()

2.设总体X在区间（0,θ）内服从均匀分布,X1,X2,X3是来自总体的简单随机样本.证明：与都是参数θ的无偏估计量,试比较其有效性.

3.设总体X服从参数为2的指数分布，X1，X2，…，Xn为来自总体X的简单随机样本，则当n→∞时，依概率收敛于_______.

4.设总体X~N(u,σ2)，u与σ2均未知，x1,x2,...,x9为其样本或样本值，检验假设H0:

更多“设总体X～N（0,σ^2）,X1,X2,…,X20是总体X的简单样本,求统计量U=所服从的分布.”相关问题

  • 第1题：

    设X1,X2,…,X7是总体X～N(0,4)的简单随机样本,求P


    答案：
    解析：
    由X1，X2…，X7与总体服从相同的分布且相互独立，得，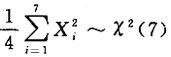
    于是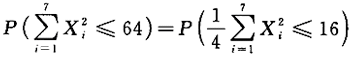
    查表得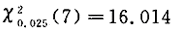，故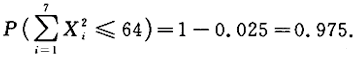

  • 第2题：

    设总体X的分布律为P（X=k)P(k=1,2,…),其中p是未知参数,X1,X2,…,Kn为来自总体的简单随机样本,求参数p的矩估计量和极大似然估计量.


    答案：
    解析：

  • 第3题：

    设总体X服从分布N(0，2^2)，而X1，X2，…，X15是来自总体X的简单随机样本，则随机变量服从_______分布，参数为________.


    答案：1、F 2、(10，5)
    解析：
    本题是数三的考题，由于X～N(0，2^2)，则　
    且相互独立，故

    答案应填服从F分布，参数为(10，5).

  • 第4题：

    设总体X的密度函数为f(x)=,X1,X2,…,Xn为来自总体X的简单随机样本,求参数θ的最大似然估计量.


    答案：
    解析：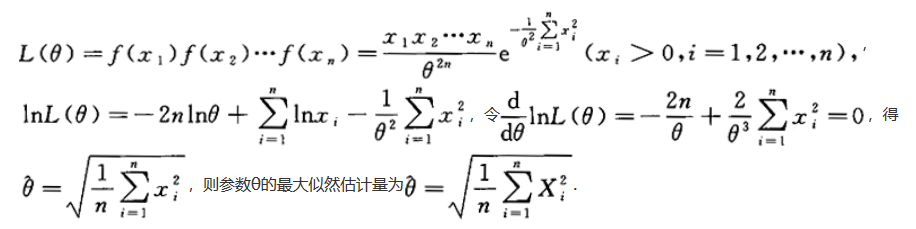

  • 第5题：

    设总体X～U(θ,θ),X1,X2,…,Xn是来自总体X的样本,求θ1,θ2的矩估计和最大似然估计.


    答案：
    解析：

  • 第6题：

    设X1,X2,…,Xn（n>2）是来自总体X～N(0,1)的简单随机样本,记Yi=Xi-（i=1,2,…,n）.求：(1)D(Yi);(2)Cov(Yb,Yn).


    答案：
    解析：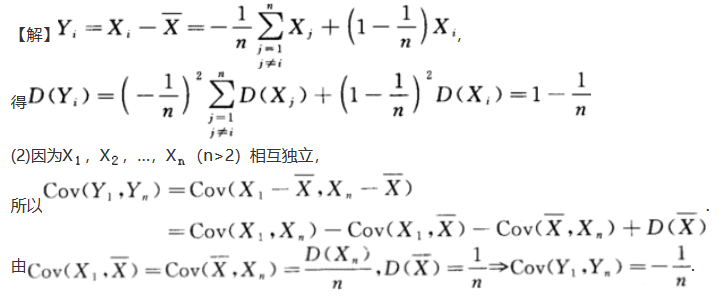

  • 第7题：

    设总体X服从正态分布N(μ，σ^2)(σ>0)，从该总体中抽取简单随机样本X1，X2，…，Xn(n≥2)，其样本均值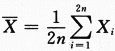,求统计量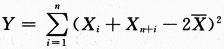的数学期望E(Y).


    答案：
    解析：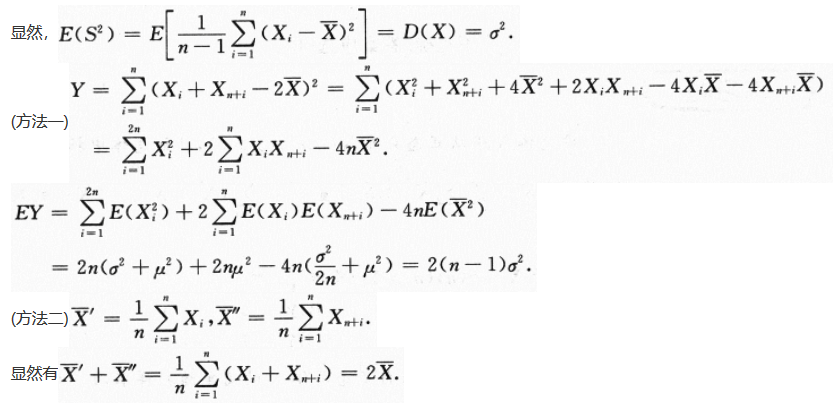

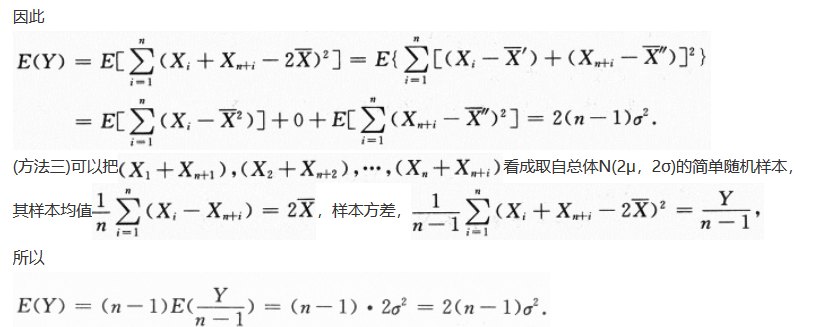
  • 第8题：

    设X1，X2，…，X9是来自正态总体X的简单随机样本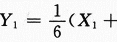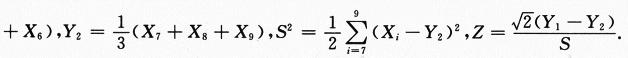，…证明统计量Z服从自由度为2的t分布.


    答案：
    解析：

  • 第9题：

    若总体X～N(0,32),X1,X2,…,x9为来自总体样本容量为9的简单随机样本,则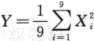服从_______分布,其自由度为_______.


    答案：
    解析：
    因为X～N(0，3)(i=1，2，…，9)，所以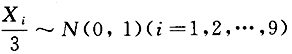且相互独立，故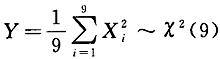，自由度为9.

  • 第10题：

    设总体X的分布函数为

    其中θ是未知参数且大于零.X1，X2，…，Xn为来自总体X的简单随机样本.
    　　(Ⅰ)求EX与EX^2；
    　　(Ⅱ)求θ的最大似然估计量.
    　　(Ⅲ)是否存在实数a，使得对任何ε>0，都有？


    答案：
    解析：
    【分析】(Ⅰ)给出F(x；θ)就有f(x；θ)，密度函数有了，就有

  • 第11题：

    设总体X的概率密度为
    　　
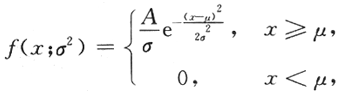
    　　其中μ是已知参数，σ>0是未知参数，A是常数.X1，X2，…，Xn是来自总体X的简单随机样本.
    　　(Ⅰ)求A；
    　　(Ⅱ)求σ的最大似然估计量.


    答案：
    解析：

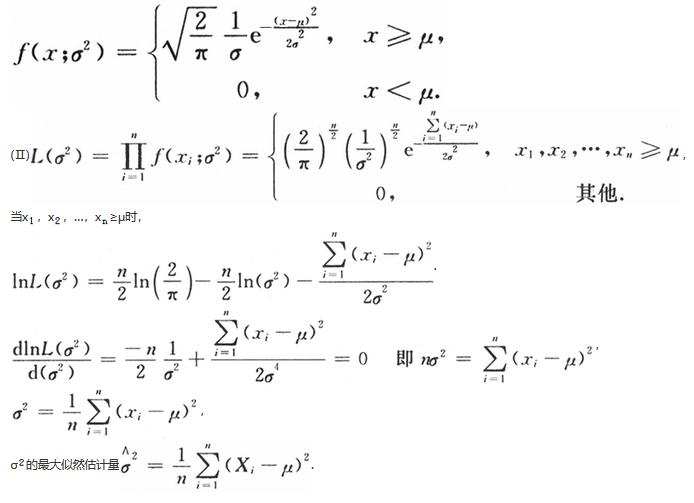
  • 第12题：

    设（X1，X2，…，X）是抽自正态总体N（0，1）的一个容量为n的样本，记，则下列结论中正确的是（）。

    • A、服从正态分布N（0，1）
    • B、n服从正态分布N（0，1）
    • C、服从自由度为n的x2分布
    • D、服从自由度为（n-1）的t分布

    正确答案:C

  • 第13题：

    设总体X的分布函数为
    　　
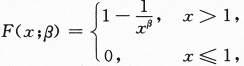
    　　其中未知参数β>1，X1，X2，…，Xn为来自总体X的简单随机样本，求：
    　　(Ⅰ)β的矩估计量；(Ⅱ)β的最大似然估计量.


    答案：
    解析：

  • 第14题：

    设总体X～N（μ,25）,X1,X2,…,X100为来自总体的简单随机样本,求样本均值与总体均值之差不超过1.5的概率


    答案：
    解析：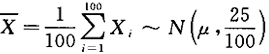
    总体均值为E(X)=μ，
    则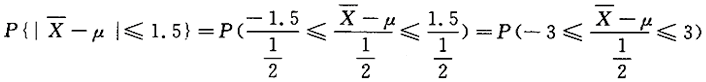
    =Ф(3)-Ф（-3）=2Ф(3)-1=0.9973

  • 第15题：

    设总体X,Y相互独立且都服从N（μ,σ^2）分布,(X1,X2,…,Xn)与(Y1,Y1,…,yn)分别为来自总体X,Y的简单随机样本,证明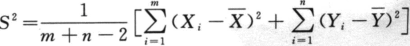：为参数σ^2的无偏估计量,


    答案：
    解析：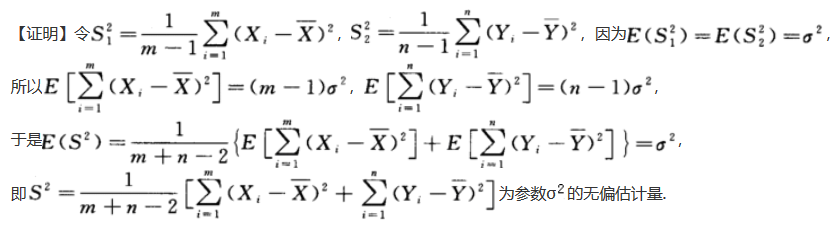

  • 第16题：

    设总体X,Y相互独立且服从N(0,9)分布,(X1,…,X9)与(Y1,…,Y9)分别为来自总体X,Y的简单随机样本,则U=～_______.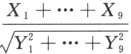


    答案：1、t(9)
    解析：

  • 第17题：

    设总体X的密度函数为f(x)=,(X1,X2,…,Xn)为来自总体X的简单随机样本.(1)求θ的矩估计量θ；(2)求D(θ).


    答案：
    解析：

  • 第18题：

    设总体X的概率密度为f(x)=,其中未知参数θ>0,设X1,X2,…,X是来自总体X的简单样本.(1)求θ的最大似然估计量；(2)该估计量是否是无偏估计量？说明理由.


    答案：
    解析：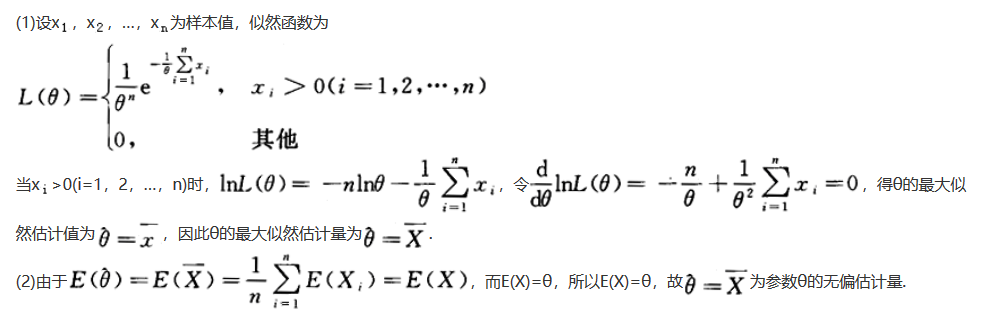

  • 第19题：

    设总体X～N（μ,σ^2）,X1,X2,…,xn为总体的简单样本,S^2为样本方差,则D(S^2)=_______.


    答案：
    解析：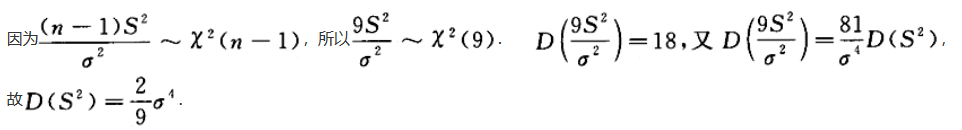

  • 第20题：

    设总体X～N(0,2^2),X1,X2,…,X30为总体X的简单随机样本,求统计量U=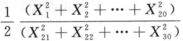所服从的分布及自由度.


    答案：
    解析：

  • 第21题：

    设总体X服从正态分布N（μ,σ^2）(σ>0),X1,X1,…,Xn为来自总体X的简单随机样本,令Y=.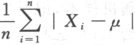,求Y的数学期望与方差


    答案：
    解析：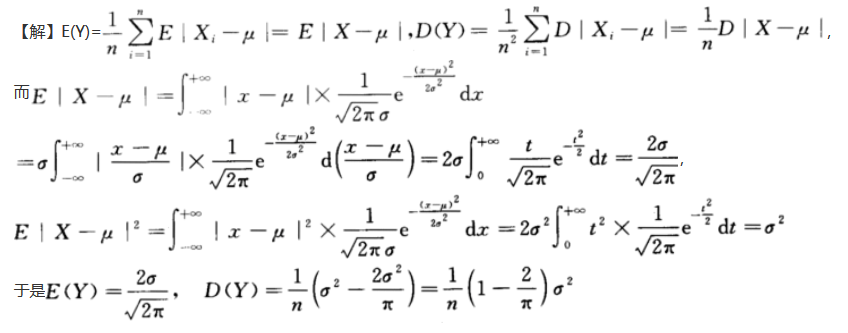

  • 第22题：

    设总体X的概率密度为
    　　
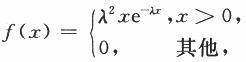
    其中参数λ(λ>0)未知，X1，X2，…，Xn是来自总体X的简单随机样本.

    (Ⅰ)求参数λ的矩估计量；

    (Ⅱ)求参数λ的最大似然估计量.


    答案：
    解析：

  • 第23题：

    设总体X~N(0,σ2)，X1，X2，...Xn是自总体的样本，则σ2的矩估计是:


    答案：D
    解析：
    提示 注意 E(x)=0，σ2=D(x)=E(x2) - [E(x)]2=E(x2)，σ2也是x的二阶原点矩，σ2的矩估计量是样本的二阶原点矩。

相关内容